2022-10-09

確率分布

確率分布とは

確率分布とは、確率実験の可能な結果とそれぞれの結果が発生する確率を表す数学的表現です。これは統計学とデータ分析の基本的な概念として機能し、不確実性をモデル化し、予測を行い、観測されたデータから未知のパラメータを推定することを可能にします。

確率分布は、店舗に到着する顧客の数、人口内の個人の身長、化学反応が完了するのにかかる時間など、さまざまな現実世界の現象をモデル化するために使用できます。異なる確率分布の特性とその基礎となる仮定を理解することで、特定の問題に適した分布を選択し、正確な推論を行うことができます。

確率分布の役割

確率分布は、記述統計学と推測統計学の両方で中心的な役割を果たしています。記述統計学では、データポイントの分布を要約して視覚化する方法を提供します。これにより、データのパターン、トレンド、および潜在的な外れ値を特定することができます。

推測統計学では、確率分布は仮説検定や信頼区間の構築の基盤として機能します。人口パラメータまたは確率変数の特定の分布を仮定することにより、テスト統計量および臨界値を導出し、データサンプルに基づいて人口に関する決定を下すのに役立ちます。

さらに、確率分布は回帰モデルや時系列モデルなどの統計モデルの開発において重要です。誤差項または応答変数の分布を指定することにより、これらのモデルのパラメータを推定し、将来の観測に関する予測を行うことができます。

確率変数

確率変数は、確率実験の各結果に実数を割り当てる関数です。言い換えると、その値は確率プロセスの結果に依存する変数です。

確率変数には、離散型と連続型の2つの主要なタイプがあります。離散型確率変数は、整数または整数などの有限または数え上げ可能な無限個の異なる値を取ります。コイントスのシリーズでの表の数や、1日に店舗に到着する顧客の数などが例です。一方、連続型確率変数は、連続的な範囲または区間内の任意の値を取ることができます。人の身長や化学反応が完了するのにかかる時間などが例です。

確率と統計において、確率変数とその実現値（または観測値または結果）を示すための慣例は次のとおりです。

$X$ 、 $Y$ 、または $Z$ などの大文字の文字は、確率変数を表すために使用されます。確率変数は、確率実験の結果を実数の集合にマップする関数です。確率変数は、確率プロセスの可能な結果の抽象的な表現であるため、大文字の文字が使用されます。
$x$ 、 $y$ 、または $z$ などの小文字の文字は、対応する確率変数の実現値、観測値、または特定の結果を示すために使用されます。小文字の文字は、確率変数が取りうる具体的な値を示します。

例えば、 $X$ がダイスを投げた結果を表す確率変数である場合、 $x$ は4を出した具体的な結果を表します。確率分布や期待値などの確率変数の特性や関数について話す場合は、大文字の文字を使用します。一方、特定の値、確率、または観測について話す場合は、小文字の文字を使用します。

離散確率分布

離散確率分布は、有限または数え上げ可能な無限個の異なる値を取る確率変数を記述します。一般的な離散確率分布には、次のものがあります。

一様分布
離散型確率変数の全ての可能な値に等しい確率を割り当てます。各結果が等しい確率で発生する状況をモデル化するためによく使用されます。
ベルヌーイ分布
成功または失敗などのバイナリの結果を、固定された成功確率で記述します。イエス・ノーの実験の単一試行をモデル化するために有用です。
二項分布
同じ成功確率を持つ独立したベルヌーイ試行の固定回数内での成功の数をモデル化します。固定回数の試行で成功する回数をモデル化するために広く使用されています。
ポアソン分布
一定の平均レートが与えられた時間または空間の固定された区間内で発生するイベントの数を表します。コールセンターへの電話の数や、バス停での到着数のようなシナリオに適用されます。
幾何分布
一連の独立したベルヌーイ試行で最初の成功を達成するまでに必要な試行回数を記述します。最初の成功までの待ち時間をモデル化するために有用です。
負の二項分布
独立したベルヌーイ試行で固定された数の成功を達成するために必要な試行回数をモデル化します。目標数の成功を達成するために必要な試行回数を分析するのに適しています。
超幾何分布
置換なしで有限集団から固定数の引き数を実行した場合の成功数を記述します。人々のグループから委員会を選択するなど、置換なしでサンプリングするシナリオで使用されます。

確率質量関数（PMF）

確率質量関数（PMF）は、離散型確率変数に関連付けられた関数であり、変数の定義域内の各可能な値に確率を割り当てます。通常、 $P(X=x)$ または $p(x)$ と表記されるPMFは、次の条件を満たす必要があります。

各値の確率は非負である（ $X$ の定義域内の全ての $x$ に対して $p(x) \geq 0$ ）
全ての可能な値の確率の合計は1である（ $\sum p(x) = 1$ ）

PMFは、様々な離散型確率分布を記述するために使用されます。与えられた分布のPMFを理解することで、確率変数に関連する確率、期待値、およびその他の関心事に関する量を計算できます。

連続型確率分布

連続型確率分布は、連続的な範囲または区間内の任意の値を取り得る確率変数を記述します。一般的な連続型確率分布には次のものがあります。

一様分布は、指定された区間内の全ての値に対して等しい確率密度を割り当てます。与えられた範囲内で一定の確率密度を持つ確率変数をモデル化するためによく使用されます。

正規分布
平均と標準偏差によって特徴付けられる鐘型分布です。中心極限定理と自然現象の多くで広く使用されるため、統計学で広く使用されています。
指数分布
イベントが一定の平均レートで連続的かつ独立して発生するポアソン過程の間の時間を記述します。待ち時間や部品の寿命をモデル化するために有用です。
ガンマ分布
さまざまな形状を取り、スキュー分布を持つ正の連続型確率変数、特に待ち時間、寿命、またはその他の正の連続型確率変数をモデル化するためによく使用されます。
ベータ分布
典型的に[0,1]の固定範囲の確率変数をモデル化し、さまざまな形状を取ることができます。確率、割合、または有限範囲で境界付けられた他の量をモデル化するために有用です。
ワイブル分布
部品の寿命または故障時間をモデル化するために使用され、信頼性工学や生存分析などで特に重要です。
対数正規分布
対数が正規分布に従う確率変数を記述します。所得や株価など、正の右偏りの分布を持つ量をモデル化するためによく使用されます。

確率密度関数（PDF）

確率密度関数（PDF）は、連続型確率変数に関連する関数であり、与えられた区間内で確率変数が値を取る確率を定義します。通常、 $f(x)$ と表されます。PDFは次の条件を満たす必要があります。

全ての値に対して確率密度が非負である（ $X$ の定義域内の全ての $x$ に対して $f(x) \geq 0$ ）
密度関数の全領域にわたる積分が1に等しい（ $\int f(x) dx = 1$ ）

PDFは、さまざまな連続型確率分布を記述するために使用されます。与えられた分布のPDFを理解することで、所望の範囲で密度関数を積分することによって、確率変数に関連する確率、期待値、およびその他の関心事に関する量を計算できます。

累積分布関数（CDF）

累積分布関数（CDF）は、離散型および連続型確率変数に関連する関数であり、確率変数が与えられた値 $x$ 以下を取る確率を表します。CDFは通常、 $F(x)$ と表され、次のように定義されます。

F(x) - P(X \leq x)

CDFには次の特性があります。

CDFは非減少関数であり、つまり $x \leq y$ に対して $F(x) \leq F(y)$ が成り立つ
CDFは右連続関数であり、任意の値 $x$ に対して、右から近づいていく限り $F(x)$ の極限が $F(x)$ に等しくなる
$x$ が負の無限大に近づく限り、 $F(x)$ の極限は0に、 $x$ が正の無限大に近づく限り、 $F(x)$ の極限は1になる

CDFは、確率変数の区間とパーセンタイルの確率を計算するのに役立ちます。CDFが与えられた場合、特定の範囲内に確率変数が存在する確率を、範囲の端点のCDF値の差を取ることによって計算できます。さらに、CDFを使用して分位数やパーセンタイルを計算することができます。分位数やパーセンタイルは、分布を等しい確率領域に分割する値です。

分位数およびパーセンタイル

分位数およびパーセンタイルは、確率変数の分布を等しい確率領域に分割する値です。確率変数 $X$ の $p$ 番目の分位数（またはパーセンタイルをパーセンテージで表した場合） $x_p$ は、 $P(X \leq x_p) = p$ となる値です。分位数およびパーセンタイルは、 $F^{-1}(p)$ というCDFの逆関数を使用して計算できます。つまり、 $x_p$ を解くことによって、次のように表されます。

x_p = F^{-1}(p)

分位数およびパーセンタイルは、データセットの分布を要約したり、モデルのパフォーマンスを評価したり、パラメータの信頼区間を推定したりするために、統計学においてさまざまな応用があります。

PMF、PDF、およびCDFの関係

離散型確率変数の場合、CDFは、 $x$ 次の全ての値のPMFの確率を合計することによって得ることができます。

F(x) = P(X \leq x) = \sum_{x_i \leq x} p(x_i)

連続型確率変数の場合、CDFは、負の無限大から与えられた値 $x$ までPDFを積分することによって得ることができます。

F(x) = P(X \leq x) = \int_{-\infty}^{x} f(t) dt

連続型確率変数の場合、PDFはCDFの $x$ に関する導関数として導出することができます。

f(x) = \frac{dF(x)}{dx}

PMF、PDF、およびCDFのプロット

この章では、Pythonを使用して、異なる確率分布のPMF、PDF、およびCDFを視覚的に理解するためにプロットします。PDFには正規分布を、PMFにはポアソン分布を使用します。両方の分布のCDFをプロットします。

まず、必要なライブラリをインポートします。

python

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm, poisson

次に、正規分布とポアソン分布のパラメータを定義します。

python

mu_normal = 0      # mean for normal distribution
sigma = 1          # standard deviation for normal distribution
lambda_poisson = 4 # lambda parameter for Poisson distribution

ポアソン分布のPMFのプロット

ポアソン分布のPMFをプロットするには、次の手順に従います。

ポアソン分布の可能な値の範囲を定義
PMFの式またはビルトイン関数（例: scipy.statsのpoisson.pmf）を使用して、各値の確率を計算
棒グラフを使用してこれらの確率をプロット

python

x_poisson = np.arange(0, 15)
y_poisson = poisson.pmf(x_poisson, lambda_poisson)

sns.set(style="whitegrid")
plt.bar(x_poisson, y_poisson)
plt.title("Poisson Distribution PMF ($\lambda = 4$)")
plt.xlabel("x")
plt.ylabel("Probability")
plt.show()

PMF

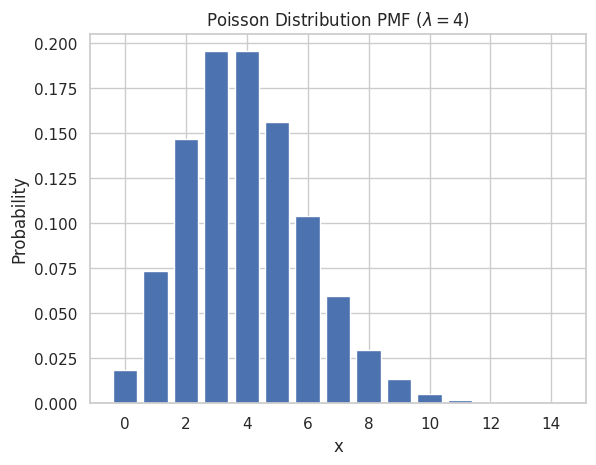
正規分布のPDFのプロット

正規分布のPDFをプロットするには、次の手順に従います。

分布の希望の範囲をカバーする均等に間隔のあるポイントの配列を作成（例: np.linspaceを使用）
PDFの式またはビルトイン関数（例: scipy.statsのnorm.pdf）を使用して、各ポイントの確率密度を計算
線グラフを使用してこれらの密度をプロット

python

x_normal = np.linspace(-5, 5, 1000)
y_normal = norm.pdf(x_normal, mu_normal, sigma)

sns.set(style="whitegrid")
plt.plot(x_normal, y_normal)
plt.title("Normal Distribution PDF ($\mu = 0$, $\sigma = 1$)")
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.show()

PDF

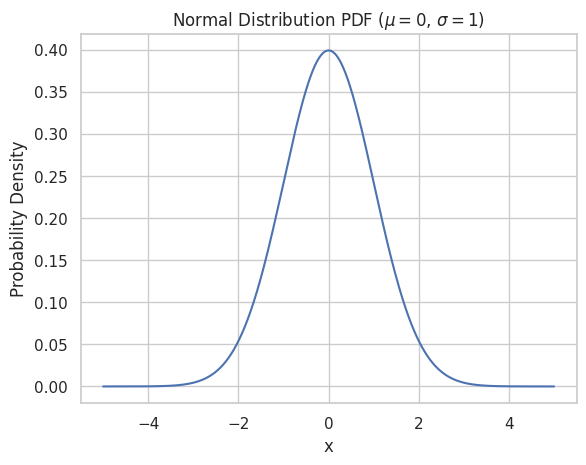
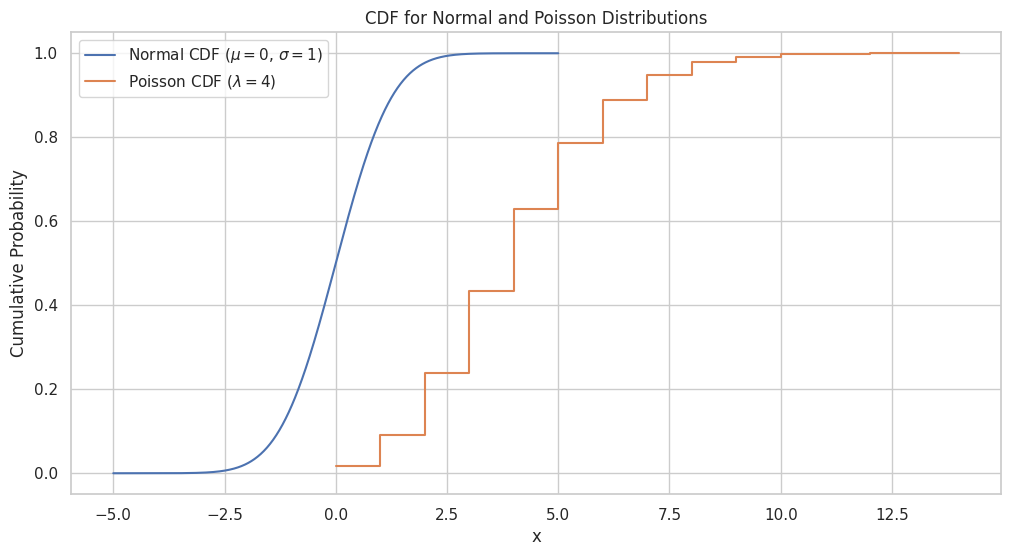
正規分布およびポアソン分布のCDFのプロット

正規分布およびポアソン分布のCDFをプロットするには、次の手順に従います。

分布の希望の範囲をカバーする均等に間隔のあるポイントの配列を作成（例: np.linspaceを使用）
CDFの式またはビルトイン関数（例: scipy.statsのnorm.cdfおよびpoisson.cdf）を使用して、各ポイントの累積確率を計算
線グラフを使用してこれらの累積確率をプロット

python

x_normal_cdf = np.linspace(-5, 5, 1000)
y_normal_cdf = norm.cdf(x_normal_cdf, mu_normal, sigma)

x_poisson_cdf = np.arange(0, 15)
y_poisson_cdf = poisson.cdf(x_poisson_cdf, lambda_poisson)

plt.figure(figsize=(12, 6))

sns.set(style="whitegrid")
plt.plot(x_normal_cdf, y_normal_cdf, label="Normal CDF ($\mu = 0$, $\sigma = 1$)")
plt.step(x_poisson_cdf,y_poisson_cdf, label="Poisson CDF ($\lambda = 4$)", where='post')
plt.title("CDF for Normal and Poisson Distributions")
plt.xlabel("x")
plt.ylabel("Cumulative Probability")
plt.legend(loc="upper left")
plt.show()