ポアソン分布とは

ポアソン分布とは、単位時間（期間）あたりに平均 \lambda 回起こる事象が k 回起こる確率が従う確率分布になります。ポワソン分布は実世界の問題によく適用されます。例えば次のような例が挙げられます。

• 1時間あたりの1人来店するレストランに1時間あたり10人来店する確率
• 1日に平均3回の交通事故が起こる交差点で今日交通事故が一回も起きない確率

確率変数 X がポアソン分布に従うとき、ある期間に平均 \lambda 回起こる事象が k 回起こる確率は次の式で求めることができます。

上式より、ポアソン分布は \lambda にのみ依存することが分かります。\lambda が1、10、20、50の場合の分布は次のようになります。

\lambda が大きくなるほど分布は正規分布に近づいていきます。

ポアソン分布の確率計算の例として、1時間に平均5人来店するレストランで、1時間に10人来客する確率を求めてみます。この場合は \lambda=5、k=10となります。次のように確率を計算します。

1時間に10人来客する確率は1.8%となりました。

二項分布との関係

二項分布は、ある事象が確率 p として n 回ある試行したときにその事象が実際に起こる回数 X が従う確率分布です。ポワソン分布は、二項分布の np を定数 \lambda として一定にし、n \to \infty、p \to 0 の極限で表すことができます。

上式のより、ある事象がポアソン分布に従うと仮定するには、確率 p が小さい値、つまり、めったに起こらない事象を扱う必要があります。そのためポアソン分布では、無限に区切ることができる時間の単位が使われることが多いです。

例として1日に2回交通事故が発生する道路があるとします。1日は86400秒なので、1日に86400回試行して2回交通事故が発生したと考えることもできます。1秒の間に交通事故が発生する確率は限りなく小さくなります。このように時間は無限に小さく区切ることができ、確率 p を限りなく0に近づけることができるためポアソン分布がよく適用されます。

ポアソン分布の期待値と分散

ポアソン分布の期待値、分散はともに \lambda になります。

ポアソン分布の再生性

確率変数 X と Y が次のようにそれぞれポアソン分布に従い、互いに独立であるとします。

このとき、ポアソン分布の再生性より、X + Y は次のポアソン分布に従います。

Python コード

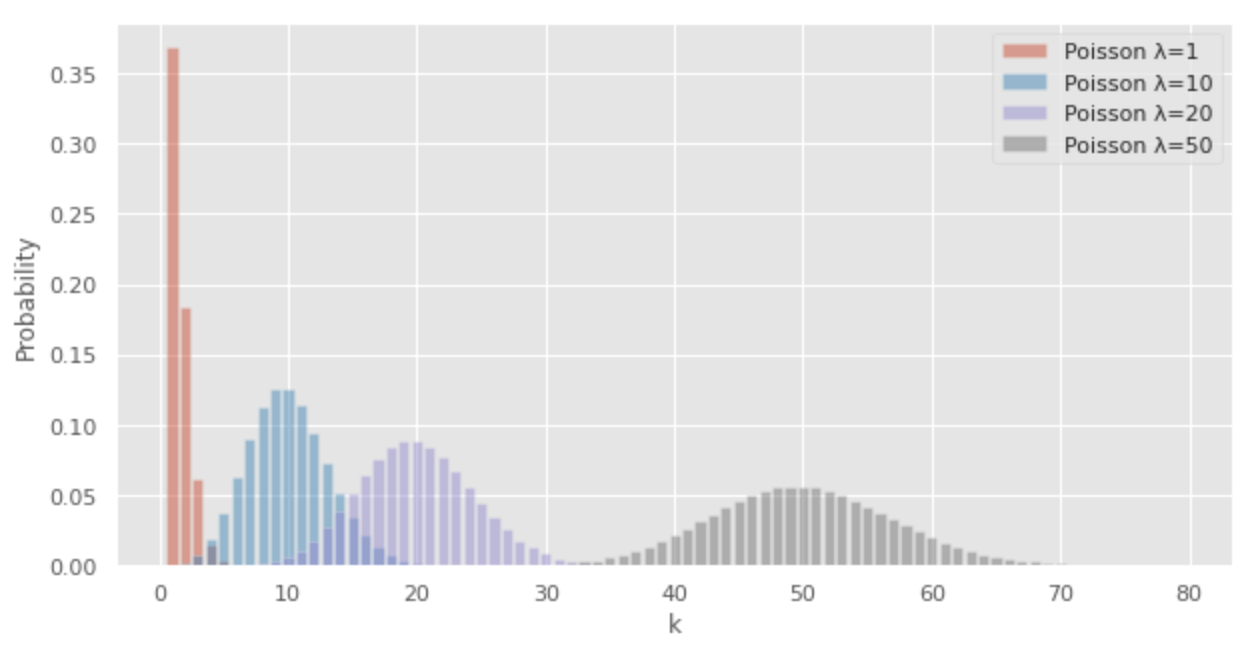
次のPythonコードでポアソン分布を描画することができます。

import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt

x =  np.arange(1, 80, 1)

# probability of the poisson distribution
y1= [poisson.pmf(i, 1) for i in x]
y10= [poisson.pmf(i, 10) for i in x]
y20= [poisson.pmf(i, 20) for i in x]
y50= [poisson.pmf(i, 50) for i in x]

# draw graph
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))
# plt.grid()

ax.bar(x,y1,alpha=0.5, label="Poisson λ=1")
ax.bar(x,y10,alpha=0.5, label="Poisson λ=10")
ax.bar(x,y20,alpha=0.5, label="Poisson λ=20")
ax.bar(x,y50,alpha=0.5, label="Poisson λ=50")

ax.legend()
ax.set_xlabel("k")
ax.set_ylabel("Probability")
plt.show()