二項分布とは

二項分布とは、ある事象が起こる確率を p として、その事象の観察を n 回行ったときにその事象が起こる回数 X が従う分布になります。二項分布は B(n,p) と表記されることもあります。

例えば、サイコロを3回（n = 3）投げて、1の目が出る（p=\frac{1}{6}）回数 X の分布は二項分布に従います。

二項分布の確率は次の式で表されます。

サイコロの例

サイコロを3回投げて1の目が出る回数の分布について考えます。

まずは事象のついて考えます。事象としては、次の2パターンになります。

• 1の目が出る
• 1の目が出ない

このように事象が発生する、しないといった2択の事象であるため、この事象が起こる確率の分布は二項分布になります。

次に事象の発生確率を考えます。１の目が出る確率、1の目が出ない確率はそれぞれ次のようになります。

サイコロを3回投げて1の目が出る回数は0回、1回、2回、3回の4パターンがあります。それぞれの確率は以下になります。

上記の確率を一般的に記述すると次の二項分布の確率の式となります。

Python で確認

Pythonを用いて B(3,\frac{1}{6}) の分布を確認してみます。コードは以下になります。サンプルサイズは1,000としています。

from scipy.stats import binom
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

data_binom = binom.rvs(n=3, p=1/6, size=1000)
plt.figure(figsize=(10,5))
sns.distplot(data_binom, kde=False)

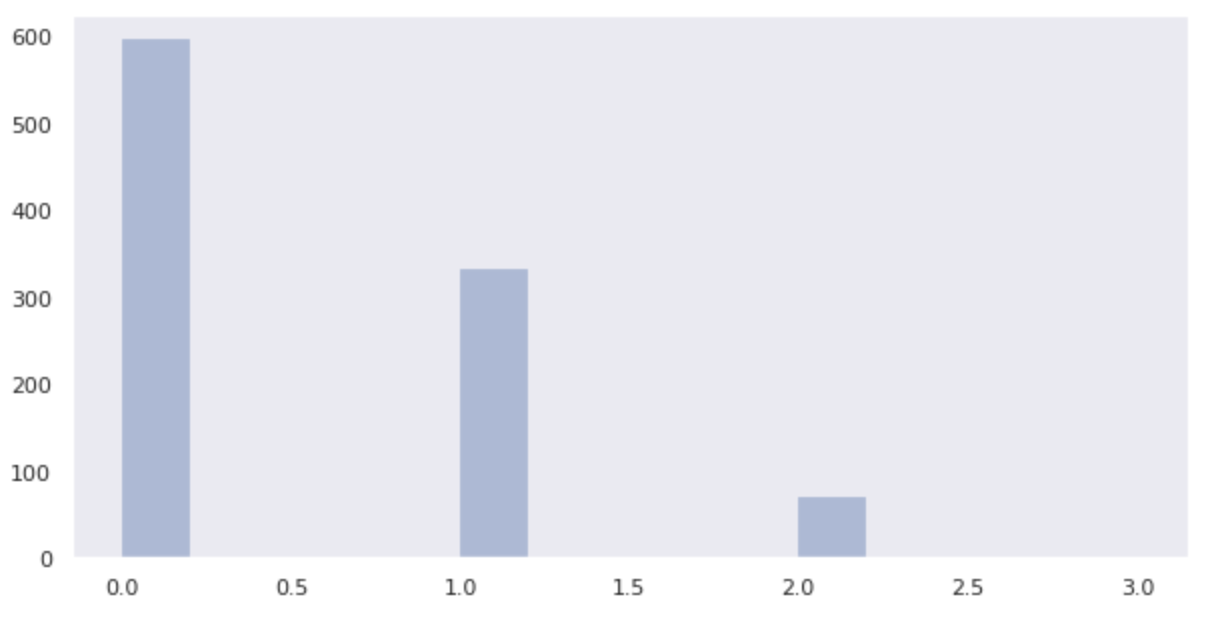
次の確率の計算値と近い確率となっていることが分かります。

ラプラスの定理

確率変数Xが二項分布 B(n,p) に従うとき、n を十分に大きくするにつれて，正規分布に近づいていきます。これをラプラスの定理といいます。

ラプラスの定理をPythonで実際に確認してみます。今回はサイコロを100回投げて1の目が出る回数の分布B(100,\frac{1}{6}) を確認します。サンプルサイズは1,000としています。

from scipy.stats import binom
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

data_binom = binom.rvs(n=100, p=1/6, size=1000)
plt.figure(figsize=(10,5))
sns.distplot(data_binom, kde=False)

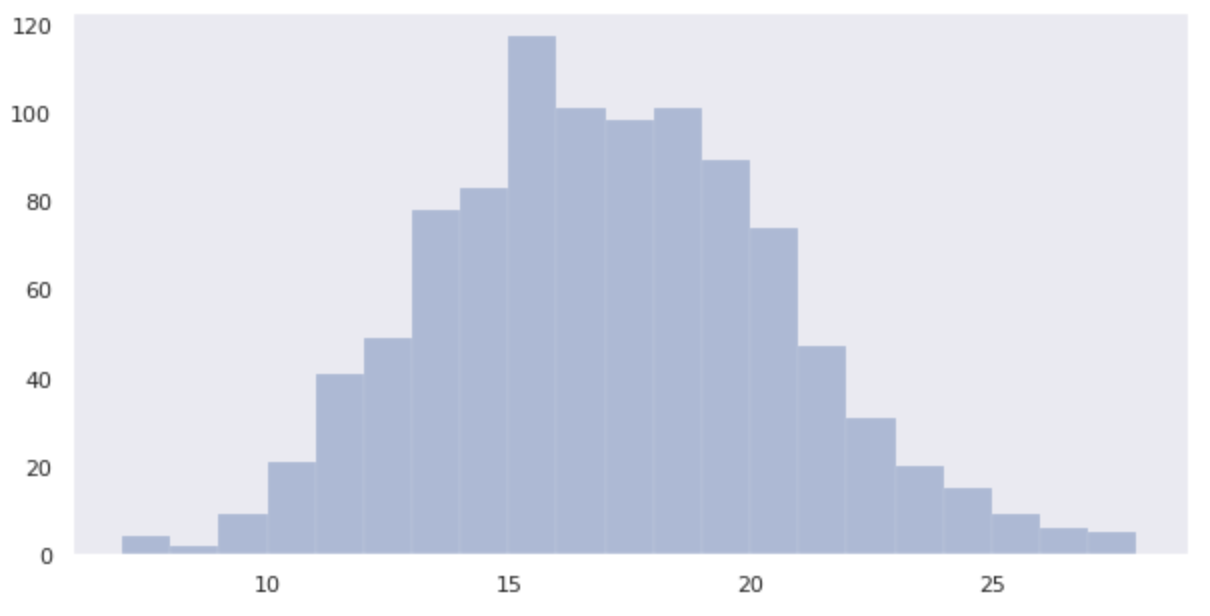
サイコロを３回投げるときよりも、より正規分布に近づいていることが分かります。