正規分布とは

正規分布（ガウス分布）とは、もっとも汎用的に活用される確率分布の一つであり、自然現象や社会現象などを表現するために利用されています。正規分布は次の基本的な性質があります。

• 平均値、中央値、最頻値が一致する
• 平均値をピークとし、平均値を中心に曲線は左右対称となる
• 標準偏差により曲線のピークや分布の幅が変化する
• x軸が漸近線である
• 曲線とx軸に囲まれた面積は1になる

正規分布の実例としては、成人男性（女性）の身長などが挙げられます。

確率密度関数

一変量の確率変数 X が平均 \mu、分散 \sigma^2 の正規分布に従うとき、その確率密度関数（RDF）は次の式で表されます。

正規分布は平均 \mu、分散 \sigma^2 に従うとき、N(\mu, \sigma^2) に従うと表現されます。また、正規分布の確率密度関数の総和は1になります。つまり、この確率密度関数を全区間で積分すると1になります。

確率密度関数の求め方

世の中の現象の多くは、平均値をピークとして平均値から遠ざかるにつれて出現確率は小さくなっていきます。これらの現象は次の関数で表現することができます。

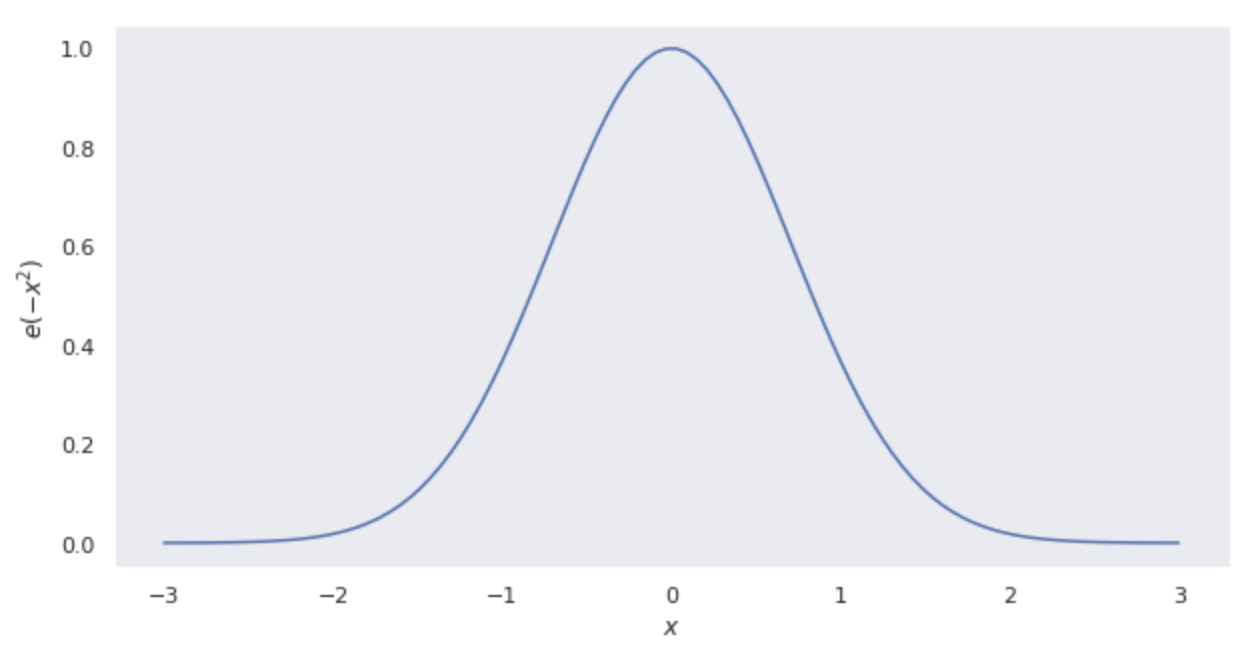
上記の関数をベースにより汎用的な関数に修正していきます。まずは任意の平均値を設定できるようにします。次のように \mu の値によって平均値を左右に平行移動できるようにします。

次に任意に分布の幅を設定できるようにするため、次の式に変形します。

\sigma の値によって分布の幅をコントロールできるようになりました。ここで、2\sigma^2 の \sigma^2 は、\sigma の値によらず、常に正の値を取るようにするために二乗されています。また、係数の2は後の積分の結果をシンプルにするためにつけられています。

密度関数は全区間の積分の和が１になります。そのため式の先頭に定数 c をつけて調整します。

上式を計算すると定数 c は次の値となります。

よって、正規分布の確率密度関数は次の式になります。

正規分布の確率

正規分布であれば、平均 \mu と標準偏差 \sigma が分かると、確率変数 X の発生確率が分かります。

下図の正規分布のグラフに標準偏差（± \sigma、±1.96 \sigma、±2 \sigma）の範囲を示しています。

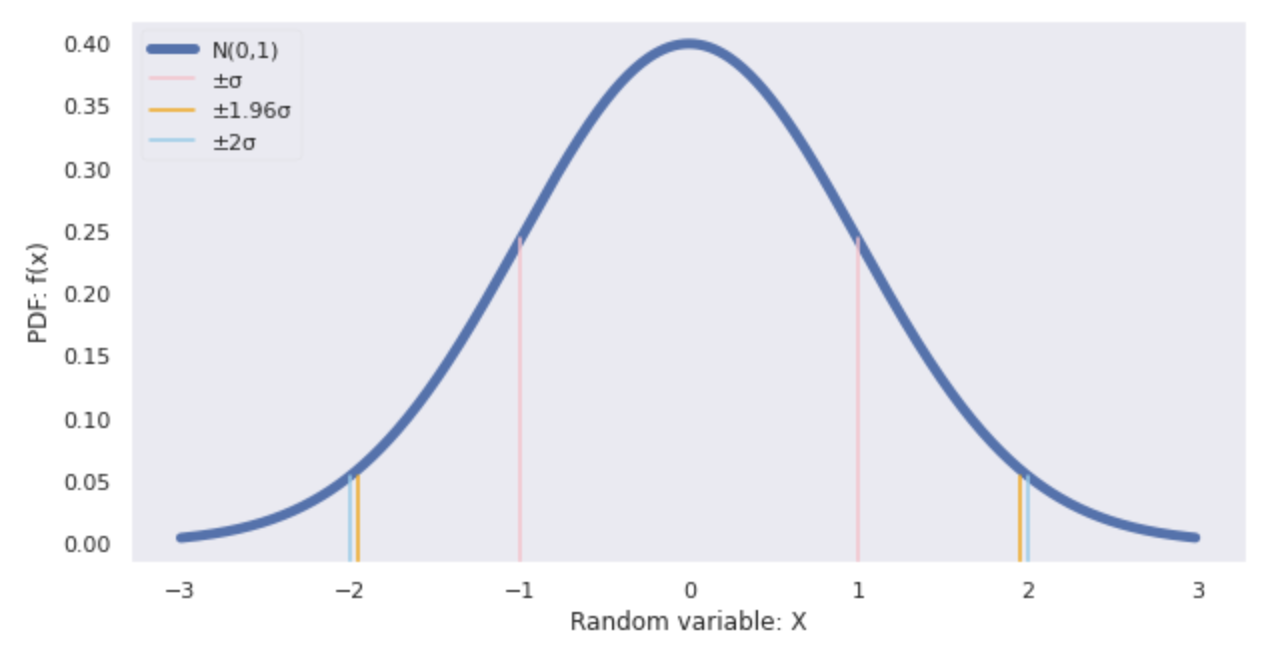
確率変数 X の範囲とその発生確率は以下になります。

仮設検定 でよく使われる1.96 \sigma は、95%の有意水準として扱われます。

標準正規分布

確率変数 X が正規分布 N(\mu,\sigma^2) に従うとき、aX+b は正規分布 N(a\mu+b,a^2\sigma^2)に従います。

この性質を利用して、Z=X−\mu\sigma と変換すると、Z は平均0、分散1の正規分布に従います。この変換を正規分布の標準化といい、平均0、分散1の正規分布を標準正規分布といいます。

正規分布の再生性

正規分布の再生性とは、確率変数 X と Y が独立に正規分布 N(\mu_1,\sigma^2_1), N(\mu_2,\sigma^2_2) にそれぞれ従うとき、X+Y の分布は正規分布 N(\mu_1+\mu_2,\sigma^2_1+\sigma^2_2) に従うという性質のことです。

例として、互いに独立な確率変数 X、Y がそれぞれ N(2, 2^2)、N(5, 3^2) に従うとして、確率変数 3X + 2Y が従う確率分布を求めます。

確率変数 3X が従う確率分布は次のようになります。

確率変数 2Y が従う確率分布は次のようになります。

正規分布の再生性より、確率変数 3X + 2Y が従う確率分布は次のようになります。

確率変数 3X + 2Y が従う確率分布は期待値16，分散72の正規分布ということになります。

Python コード

今回の記事で使用したPythonコードは以下になります。

y=e^{-x^2}を描画

```python
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from matplotlib import rcParams
rcParams['figure.figsize'] = 10, 5
# %matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

x = np.linspace(-3, 3, 100)
y = np.exp(x)

plt.figure()
plt.plot(x, np.exp(-x**2))
plt.xlabel('$x$')
plt.ylabel('$-\exp(-x^2)$')

plt.show()

正規分布を描画

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from matplotlib import rcParams
rcParams['figure.figsize'] = 10, 5
# %matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

# normal distribution setting
mean = 0
std  = 1

# set random variable
X = np.arange(-3,3,0.01)

# calculate PDF
Y = stats.norm.pdf(X,mean,std)

# draw normal distribution
plt.plot(X,Y,label="N(0,1)", linewidth=5)

# draw standard deviation
plt.axvline(x=std, color="pink", ymax=1.5*Y.max(), label="±σ")
plt.axvline(x=-std, color="pink", ymax=1.5*Y.max())
plt.axvline(x=1.96*std, color="orange", ymax=0.4*Y.max(), label="±1.96σ")
plt.axvline(x=-1.96*std, color="orange", ymax=0.4*Y.max())
plt.axvline(x=2*std, color="skyblue", ymax=0.4*Y.max(), label="±2σ")
plt.axvline(x=-2*std, color="skyblue", ymax=0.4*Y.max())

# graph setting
plt.xlabel("Random variable: X")
plt.ylabel("PDF: f(x)")
plt.legend(loc="upper left")
plt.show()