仮説検定とは
仮説検定(hypothesis Testing)とは、ある母集団に対して仮説を立て、標本を用いてその仮説の真偽を統計学的に検証するという推計統計学の手法の一つになります。仮説検定では、対立仮説という主張したい仮説と、その主張と相容れない仮説として帰無仮説を仮定し、帰無仮説が棄却、つまりは否定することで、背理法的に対立仮説が成立するとみなします。
仮説検定の手順
仮説検定は次の手順で実施されます。
- 帰無仮説、対立仮説の設定
- 検定統計量の算出(検定の選択)
- 有意水準 α の設定(棄却域の設定)
- 帰無仮説の棄却または採択
帰無仮説、対立仮説の設定
仮説が正しいと仮定した場合にその標本が観察される確率を算出できるように、仮説を統計学的に表現します。検定は次の二者択一となり、帰無仮説を棄却できるかどうかを検証することが目的になります。
- 帰無仮説
帰無仮説は正しいかどうかの判断のために立てられる仮説になります。帰無仮説をもとに検定を実施し結論を導きます。帰無仮説はH_0 - 対立仮説
対立仮説は帰無仮説に対立する仮説で、帰無仮説が棄却された際に採択されます。本来証明したい仮説を対立仮説として立てます。対立仮説はH_1
例えば、薬の効果を有意的に主張できるかを検定したい場合、帰無仮説と対立仮説はそれぞれ次のように設定します。
- 帰無仮説(
H_0 - 対立仮説(
H_1
ここで、仮説検定は帰無仮説の棄却をし、主張したいことの正しさの証明を目指す検定であるため、必ず主張したい仮説を対立仮説にし、主張したい仮説ではない方の仮説を帰無仮説とする必要があります。
仮説検定が帰無仮説を棄却することで立てた仮説(対立仮説)の正しさを説明するという手法をとる理由は次の2点が考えられます。
- 対立仮説を直接的に立証することが難しい場合があるため
- 容易に対立仮説を選択しないようにするため
一つ目の理由について、対立仮説は確率の計算ができない場合があります。例えばあるコインの裏表が出る確率が1/2でないと疑っているとして、帰無仮説と対立仮説はそれぞれ次のようになります。
- 帰無仮説(
H_0 - 対立仮説(
H_1
ここで、コインの裏表が出る確率を計算するには、いったんは確率を1/2とする、つまり帰無仮説が正しいと仮定しないと確率の計算ができません。そこで、確率の計算が可能な帰無仮説を正しいと仮定し、帰無仮説を統計的に否定することで対立仮説を立証するという流れになります。
二つ目の理由について、検定には α エラーと β エラーという二つの誤りがあります。
| 帰無仮説が正しい | 対立仮説が正しい | |
|---|---|---|
| 帰無仮説を棄却する | α エラー | OK |
| 帰無仮説を採択する | OK | β エラー |
α エラーと β エラーのどちらが重要な誤りかは場合によりますが、β エラーの場合は少なくとも結論が現状維持されます。α エラーを起こりにくくするため有意水準を厳しく設定することで容易に対立仮説を採択しないようにするというのが仮説検定の考え方になります。
検定統計量の算出(検定の選択)
検定統計量とは、仮説検定のために標本から一定のルールに従って算出された統計量のことです。検定統計量の算出方法は母集団の分布や検定する母数により異なります。
代表的な検定統計量としてT検定、F検定、Z検定、カイ二乗検定などが挙げられます。
| 検定名 | 検定統計量 | 目的 |
|---|---|---|
| T 検定 | t 値 | 2 つの母集団の平均が有意に異なるどうか |
| F 検定 | f 値 | 2 つの母集団の標準偏差が有意に異なるどうか |
| Z 検定 | z 値 | 標本の平均と母集団の平均とが統計的に有意に異なるかどうか |
| カイ二乗検定 | カイ二乗値 | 2 つの変数に対する 2 つの観察が互いに独立かどうか(独立性)、観測された度数分布が理論分布と同じかどうか(適合度) |
有意水準 α の設定(棄却域の設定)
帰無仮説が正しいとして、検定統計量の分布全体を棄却域(Rejection Region)と採択域(Acceptance Region)に分割し、帰無仮説が棄却域に入る確率を検定の有意水準とします。つまり有意水準は帰無仮説が誤りであると判定するための基準となる確率になります。有意水準は大抵1%や5%といった小さな値を設定します。
検定の際には、検定統計量が棄却域に入る、つまり検定を行う分布からはめったに生じない事象が発生したということにより帰無仮説を棄却するという結論となります。検定統計量が棄却域に入り帰無仮説を棄却したとき、統計的に有意であるという表現が用いられます。
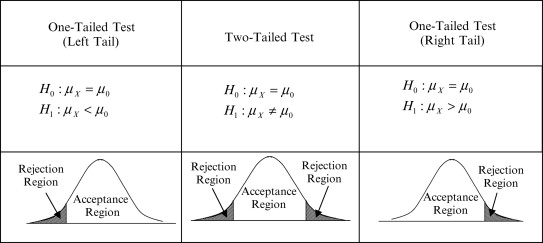
検定には両側検定(Two-Tailed Test)と片側検定(One-Tailed Test)があります。
片側検定は左側または右側の確率だけで有意水準 α とする検定方法であり、片側だけで有意水準 α とするため、棄却域は同じ有意水準での両側検定よりも広くなります。つまり、片側検定の方が両側検定より帰無仮説を棄却しやすくなります。例えば、有意水準α=0.05とすると、両側検定の場合は棄却域が左右2.5%ずつであるのに対して、片側検定の棄却域は左右どちらかの5%になります。
片側検定は次のような場合に行います。
- 標本平均が明らかに特定の値より大きくなる(小さくなる)ことが分かっている場合
- 標本平均が特定の値より大きいこと(小さいこと)のみを調べたい場合
帰無仮説の棄却または採択
算出した検定統計量が棄却内にあるかどうかを判定します。通常は、算出した検定統計量と同じかそれよりも極端に仮説に反する値となる確率
一方、検定統計量が棄却域外にある場合は、帰無仮説を棄却するには証拠不十分となり、帰無仮説は棄却出来ずに検定は失敗に終わります。つまり、この場合は帰無仮説と対立仮説のどちらが正しいかは分からないままになります。仮説検定は、対立仮説が正しいという主張を統計的に明らかにするために、対立する帰無仮説を棄却するという手法なので、帰無仮説が正しいと証明する検定ではないためこのような終着となります。
仮説検定の例
今回は、駅前ハンバーガー店のフライドポテトの重量は公表値の135gの通りであるかどうかを、仮説検定を実施して検証します。
まずは仮説を考えます。フライドポテトの重量が公表値通りでないと疑っているとすると、帰無仮説と対立仮説はそれぞれ次のようになります。
- 帰無仮説(
H_0 - 対立仮説(
H_1
駅前のハンバーガー店でフライドポテトを10個購入し、各フライドポテトの重量を計測した結果、次のようになったとします。
- 130g
- 140g
- 124g
- 120g
- 133g
- 126g
- 131g
- 132g
- 130g
- 134g
標本平均
次に検定統計量を算出します。今回は母分散が既知で
- 母分散が未知
- サンプルサイズが30未満
駅前のハンバーガー店のフライドポテトの重量は正規分布に従っているとすると、購入した10個(n=10)のフライドポテトの標本平均は、母平均を
次に有意水準を設定します。今回はもっとも一般的な値である有意水準 α=0.05として扱います。ここで、フライドポテトの重量が公表値の135gであるかどうかの検定なので、両側検定を採用します。
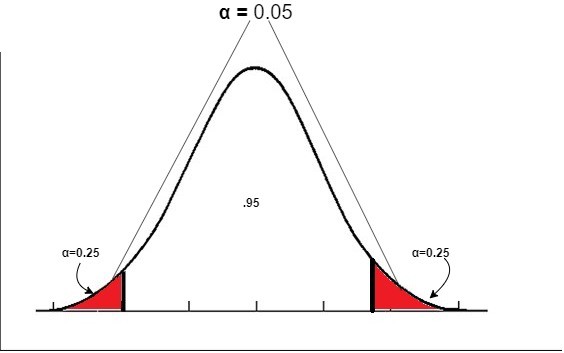
Hypothesis Testing — 2-tailed test
上図の赤の部分が棄却域になります。棄却域は全体の5%であり、両端の棄却域はそれぞれ2.5%を占めています。
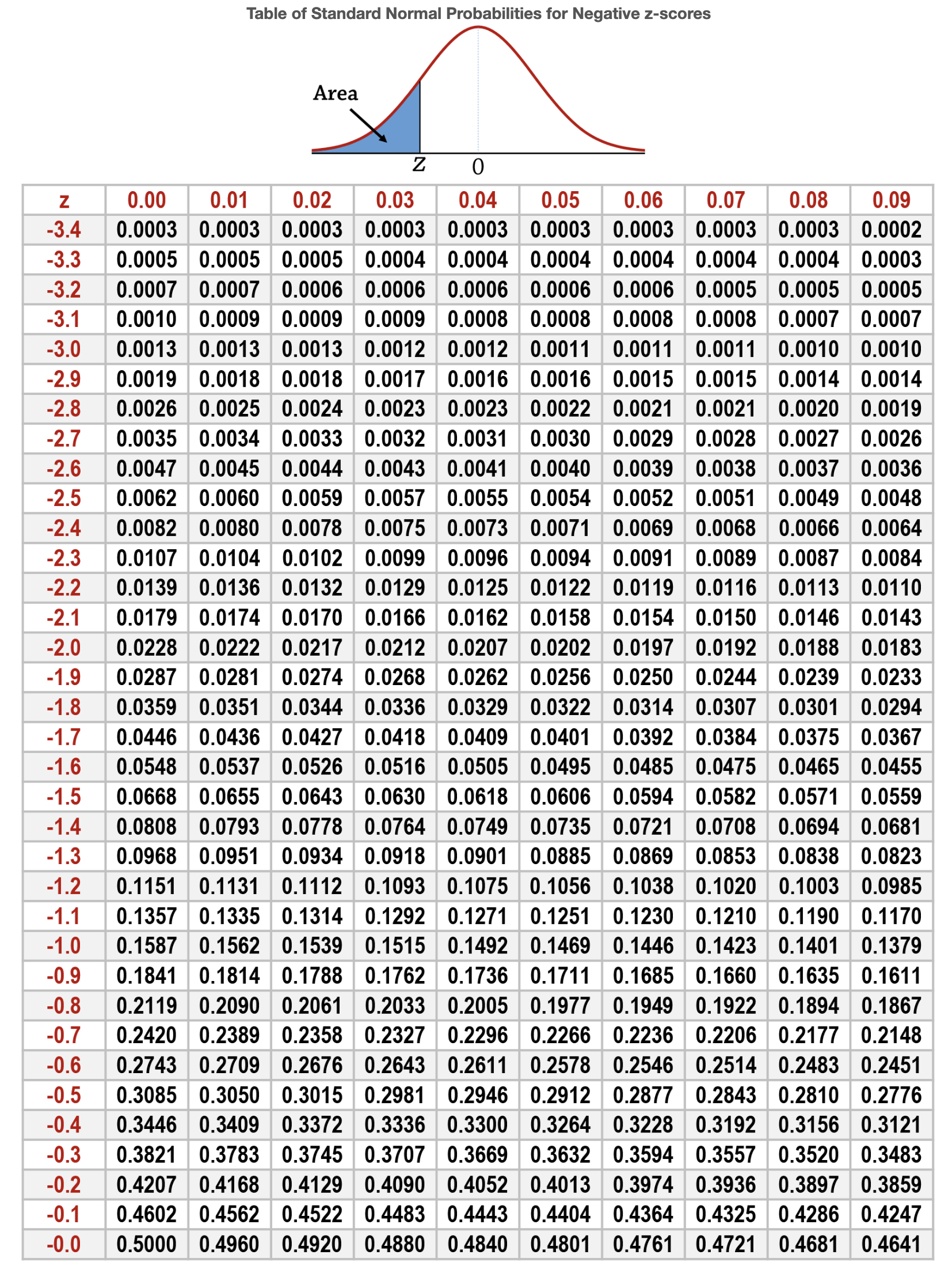
最後にp値を求めます。検定統計量Zは標準正規分布に従うため、次の標準正規分布表から検定統計量z = -2.64に対応する値を確認します。
検定統計量z = -2.64の値は0.0041となっています。今回は両側検定ですのでp = 0.0082となります。p < α となっていることから、設定した仮説のもとで観察された事象が起こることは非常にまれなことであると判断できます。
よって、検証の結果、帰無仮説「駅前のハンバーガー店のフライドポテトの重量が公表値の135gの通りである。」は棄却され、対立仮説「駅前のハンバーガー店のフライドポテトの重量が公表値の135gではない。」を採択するという結論になります。
参考