幾何分布とは

幾何分布とは、ある事象が起こる確率を p として、その事象が起こるまでの回数が従う確率分布です。幾何分布は次のような例に用いられます。

• コインを投げて表が出るまでの回数
• スリーポイントの成功率が3割のバスケットボール選手がスリーポイントを決めるまでに打つシュートの回数

確率変数 X が幾何分布に従うとき、事象の発生確率 p の試行において k 回目で初めてその事象が発生する確率は次の式で表されます。

幾何分布は X \sim Geo(p) と表記されることもあります。

p が0.05、0.1、0.5の場合の幾何分布は次のようになります。

例えば、コインを投げて3投目で初めて表が出る確率は次のように求めることができます。

3投目で初めて表が出る確率は12.5%であることが分かりました。

二項分布との関係

二項分布とは、ある事象が起こる確率を p として、その事象の観察を n 回行ったときにその事象が起こる回数が従う確率分布です。一方、幾何分布は、ある事象が起こる確率を p として、その事象が起こるまでの回数が従う確率分布です。

つまり、同じ事象を二項分布は「回数」で捉え、幾何分布は「時間・間隔」で捉えます。

また、幾何分布は、確率 p のベルヌーイ分布に従う確率変数 X_1,X_2,... において、 X_1=X_2=...=X_{n-1}=0, X_n=1 となるときの n の値ということが言えます。

幾何分布の期待値と分散

確率変数 X が成功確率 p の幾何分布に従うとき，その期待値と分散は次のようになります。

幾何分布の無記憶性

確率変数 X が幾何分布に従い、m, n > 0 とすると、次の式が成り立ちます。

上式は将来の事象発生までの時間がその過去の事象の有無に依存しないということを意味しています。例えばコインを3回投げるときに、2投目までが全て表だったとしても、その結果が3投目に表が出る確率には一切影響しないということになります。この性質を無記憶性（Memoryless）といいます。幾何分布は無記憶性を持つ唯一の離散分布になります。

Python コード

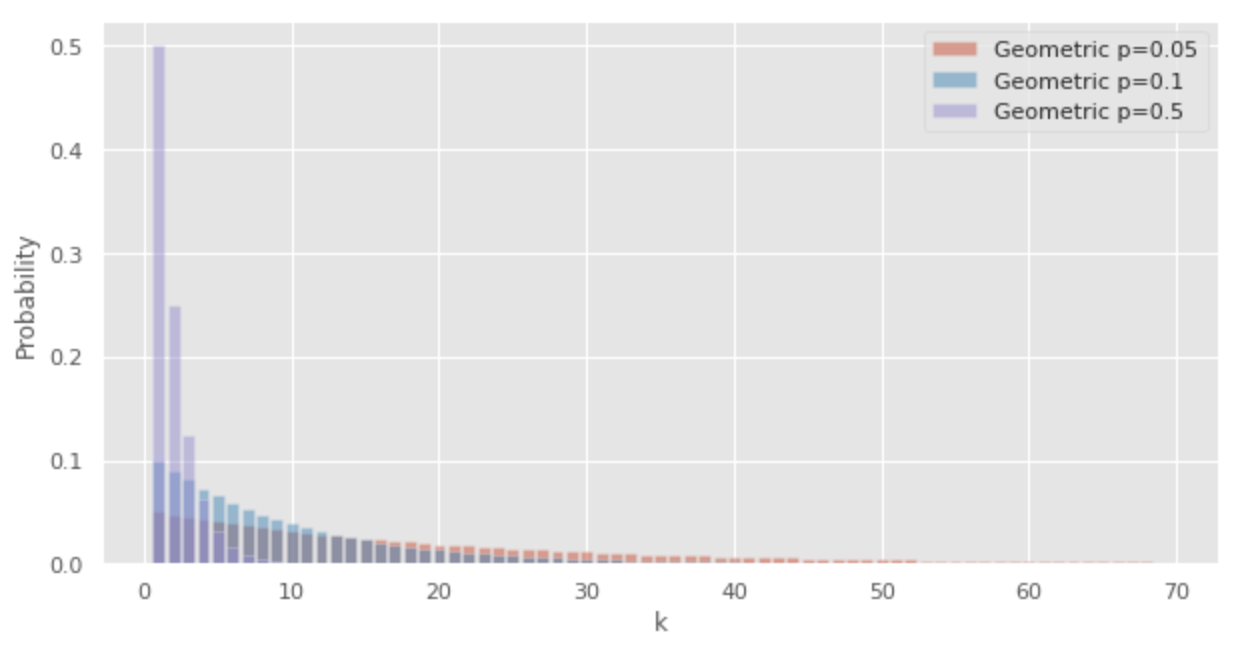
次のPythonコードで幾何分布を描画することができます。

import numpy as np
from scipy.stats import geom
import matplotlib.pyplot as plt

x =  np.arange(1, 70, 1)

# probability of the geometric distribution
y005= [geom.pmf(i, 0.05) for i in x]
y01= [geom.pmf(i, 0.1) for i in x]
y05= [geom.pmf(i, 0.5) for i in x]

# draw graph
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

ax.bar(x,y005,alpha=0.5, label="Geometric p=0.05")
ax.bar(x,y01,alpha=0.5, label="Geometric p=0.1")
ax.bar(x,y05,alpha=0.5, label="Geometric p=0.5")

ax.legend()
ax.set_xlabel("k")
ax.set_ylabel("Probability")
plt.show()