ガンマ分布とは
ガンマ分布はある期間
- 人の体重
- ウイルスの潜伏期間
- システムダウンまでの待ち時間
- 電子部品の寿命
ガンマ分布の確率密度関数は次の式で表されます。
ガンマ分布は下図が示す通り、
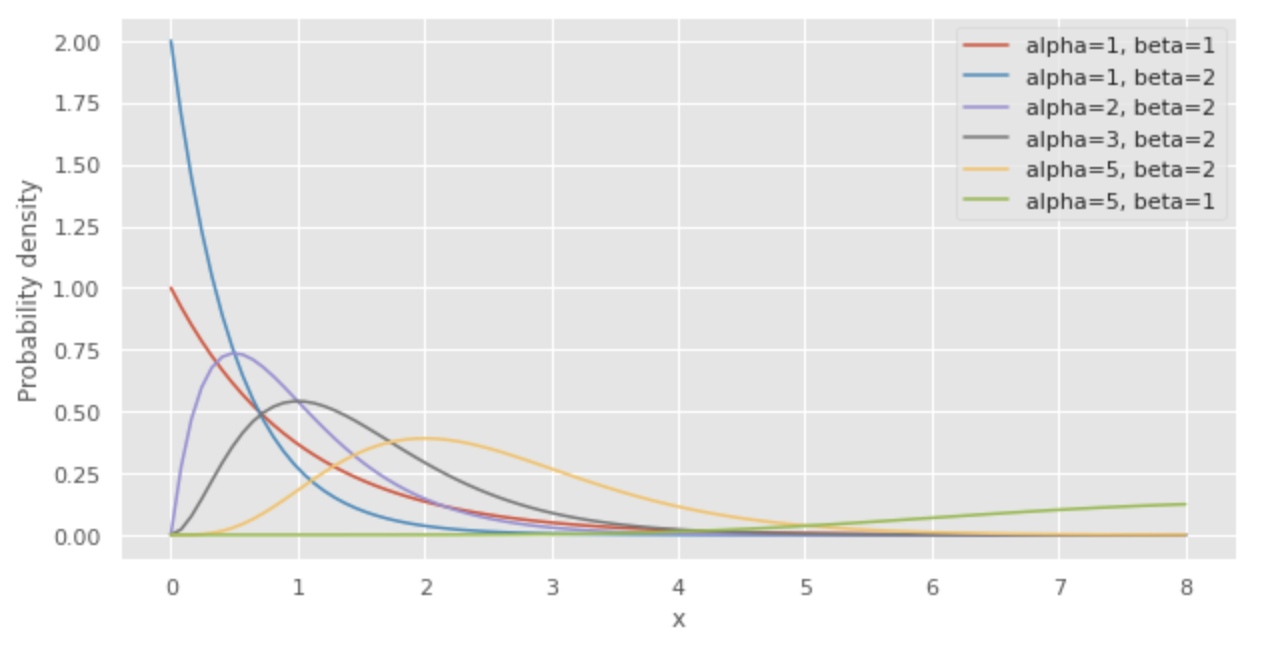
指数分布との関係
指数分布は
ガンマ分布に
上式は、期待値が
ガンマ分布の期待値と分散
ガンマ分布の期待値、分散はそれぞれ以下になります。
ガンマ分布のパラメータの影響
パラメータ
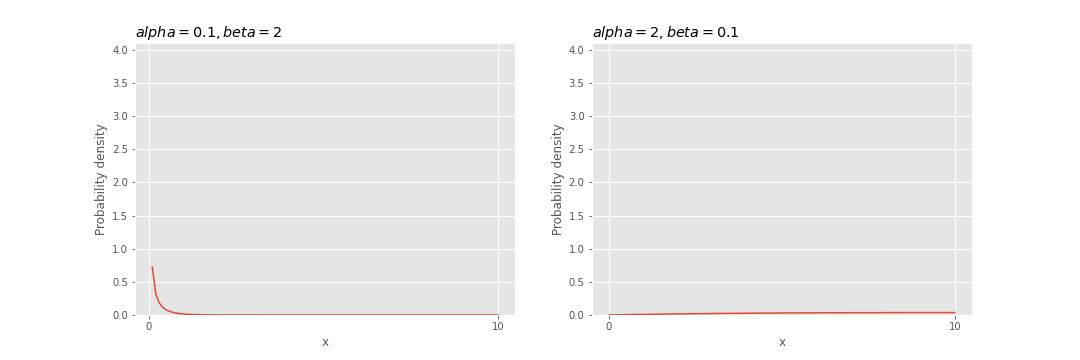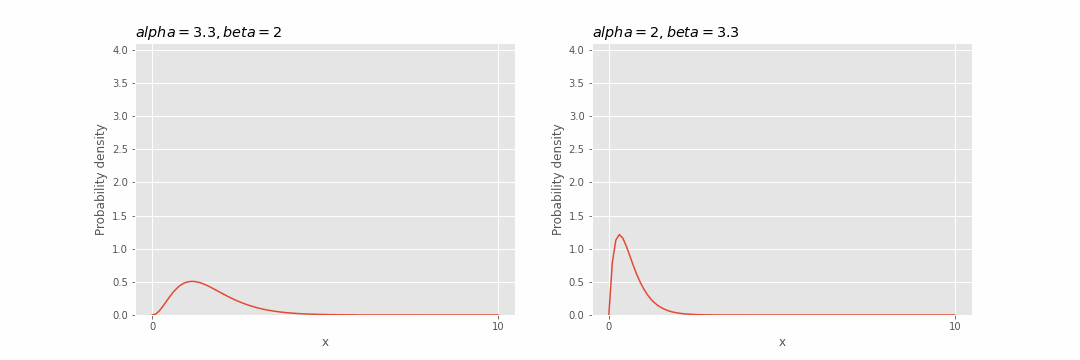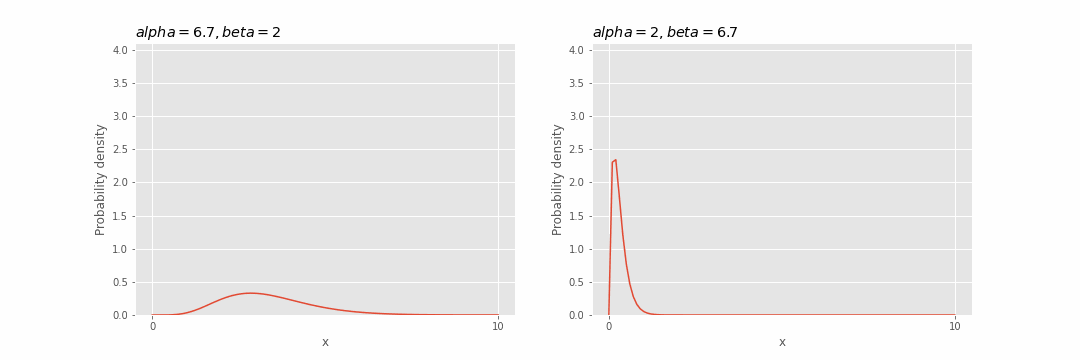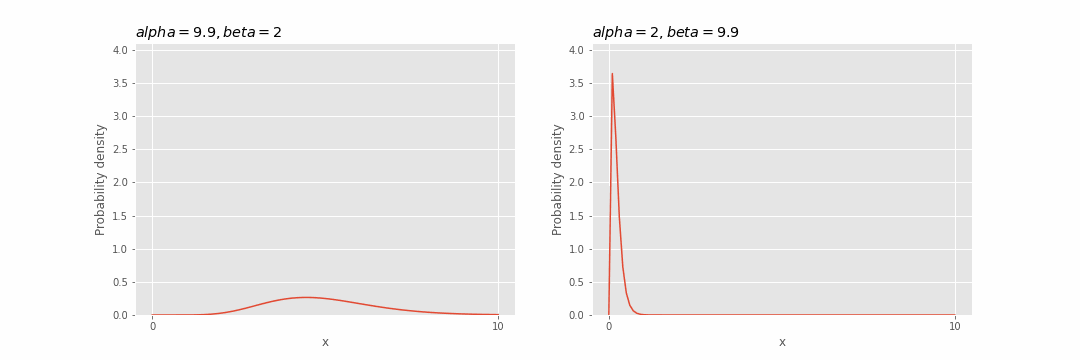
ガンマ分布の再生性
確率変数
このとき、ガンマ分布の再生性より、
Python コード
今回使用したPythonコードは以下になります。
ガンマ分布の描画
import numpy as np
from scipy.stats import gamma
import matplotlib.pyplot as plt
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))
# x axis
x = np.linspace(0, 8, 100)
# draw graph
plt.plot(x, gamma.pdf(x, 1, 0, scale=1/1), label='alpha=1, beta=1')
plt.plot(x, gamma.pdf(x, 1, 0, scale=1/2), label='alpha=1, beta=2')
plt.plot(x, gamma.pdf(x, 2, 0, scale=1/2), label='alpha=2, beta=2')
plt.plot(x, gamma.pdf(x, 3, 0, scale=1/2), label='alpha=3, beta=2')
plt.plot(x, gamma.pdf(x, 5, 0, scale=1/2), label='alpha=5, beta=2')
plt.plot(x, gamma.pdf(x, 10, 0, scale=1/1), label='alpha=5, beta=1')
plt.legend()
plt.xlabel("x")
plt.ylabel("Probability density")
plt.show()

パラメータの影響の描画
import numpy as np
from scipy.stats import gamma
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from matplotlib.animation import FuncAnimation
rc('animation', html='html5')
np.random.seed(5)
# Set up formatting for the movie files
Writer = animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)
prob_vals = np.arange(start=0.1, stop=10.01, step=0.2)
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(15, 5))
# x axis
x = np.linspace(0, 10, 100)
def update(i):
p = prob_vals[i]
# alpha graph
plt.subplot(1, 2, 1)
plt.cla()
plt.plot(x, gamma.pdf(x, round(p, 1), 0, scale=1/2))
# plt.plot(x, gamma.pdf(x, 2, 0, scale=1/round(p, 1)))
plt.title(f'$alpha={str(round(p, 1))}, beta=2$', loc='left')
plt.xlabel("x")
plt.ylabel("Probability density")
plt.ylim(0, 4.1)
plt.xticks(ticks=[0, 10]) # x axis ticks
# beta graph
plt.subplot(1, 2, 2)
plt.cla()
plt.plot(x, gamma.pdf(x, 2, 0, scale=1/round(p, 1)))
plt.title(f'$alpha=2, beta={str(round(p, 1))}$', loc='left')
plt.xlabel("x")
plt.ylabel("Probability density")
plt.ylim(0, 4.1)
plt.xticks(ticks=[0, 10]) # x axis ticks
anime_prob = FuncAnimation(fig, update, frames=len(prob_vals), interval=1000)
anime_prob.save('gamma_dist.gif', writer='pillow', fps=10)

AlloyDB
Amazon Cognito
Amazon EC2
Amazon ECS
Amazon QuickSight
Amazon RDS
Amazon Redshift
Amazon S3
API
Autonomous Vehicle
AWS
AWS API Gateway
AWS Chalice
AWS Control Tower
AWS IAM
AWS Lambda
AWS VPC
BERT
BigQuery
Causal Inference
ChatGPT
Chrome Extension
CircleCI
Classification
Cloud Functions
Cloud IAM
Cloud Run
Cloud Storage
Clustering
CSS
Data Engineering
Data Modeling
Database
dbt
Decision Tree
Deep Learning
Descriptive Statistics
Differential Equation
Dimensionality Reduction
Discrete Choice Model
Docker
Economics
FastAPI
Firebase
GIS
git
GitHub
GitHub Actions
Google
Google Cloud
Google Search Console
Hugging Face
Hypothesis Testing
Inferential Statistics
Interval Estimation
JavaScript
Jinja
Kedro
Kubernetes
LightGBM
Linux
LLM
Mac
Machine Learning
Macroeconomics
Marketing
Mathematical Model
Meltano
MLflow
MLOps
MySQL
NextJS
NLP
Nodejs
NoSQL
ONNX
OpenAI
Optimization Problem
Optuna
Pandas
Pinecone
PostGIS
PostgreSQL
Probability Distribution
Product
Project
Psychology
Python
PyTorch
QGIS
R
ReactJS
Regression
Rideshare
SEO
Singer
sklearn
Slack
Snowflake
Software Development
SQL
Statistical Model
Statistics
Streamlit
Tabular
Tailwind CSS
TensorFlow
Terraform
Transportation
TypeScript
Urban Planning
Vector Database
Vertex AI
VSCode
XGBoost