Apa itu Distribusi Probabilitas

Distribusi probabilitas adalah representasi matematika yang menjelaskan kemungkinan hasil yang mungkin dari suatu eksperimen acak dan peluang masing-masing hasil terjadi. Distribusi probabilitas berfungsi sebagai konsep fundamental dalam bidang statistik dan analisis data, memungkinkan kita untuk memodelkan ketidakpastian, membuat prediksi, dan menyimpulkan parameter yang tidak diketahui dari data yang diamati.

Distribusi probabilitas dapat digunakan untuk memodelkan berbagai fenomena dunia nyata, seperti jumlah pelanggan yang datang ke sebuah toko, tinggi individu dalam populasi, atau waktu yang dibutuhkan untuk suatu reaksi kimia selesai. Memahami sifat-sifat distribusi probabilitas yang berbeda dan asumsi dasarnya memungkinkan kita untuk memilih distribusi yang tepat untuk suatu masalah tertentu dan membuat inferensi yang akurat.

Peran Distribusi Probabilitas dalam Statistik

Distribusi probabilitas memainkan peran sentral dalam statistik deskriptif dan inferensial. Dalam statistik deskriptif, distribusi probabilitas menyediakan cara untuk merangkum dan memvisualisasikan distribusi titik data. Ini memungkinkan kita mengidentifikasi pola, tren, dan outlier potensial dalam data.

Dalam statistik inferensial, distribusi probabilitas berfungsi sebagai dasar untuk pengujian hipotesis dan konstruksi interval kepercayaan. Dengan mengasumsikan distribusi tertentu untuk parameter populasi atau variabel acak, kita dapat menghasilkan statistik uji dan nilai kritis yang membantu kita membuat keputusan tentang populasi berdasarkan sampel data.

Selain itu, distribusi probabilitas sangat penting dalam pengembangan model statistik, seperti model regresi dan model deret waktu. Dengan menentukan distribusi dari kesalahan atau variabel respon, kita dapat memperkirakan parameter dari model ini dan membuat prediksi tentang observasi di masa depan.

Variabel Acak

Variabel acak adalah fungsi yang menugaskan bilangan riil pada setiap hasil dari suatu percobaan acak. Dalam kata lain, variabel acak adalah variabel yang nilainya tergantung pada hasil dari suatu proses acak.

Ada dua jenis variabel acak utama: diskrit dan kontinu. Variabel acak diskrit mengambil himpunan nilai terbatas atau terhitung tak terbatas dari nilai-nilai yang berbeda, seperti bilangan bulat atau angka bulat. Contohnya adalah jumlah kepala pada serangkaian lemparan koin atau jumlah pelanggan yang datang ke sebuah toko dalam sehari. Variabel acak kontinu, di sisi lain, dapat mengambil nilai apa saja dalam rentang atau interval yang kontinu, seperti tinggi seseorang atau waktu yang dibutuhkan untuk suatu reaksi kimia selesai.

Dalam probabilitas dan statistik, konvensi untuk menandai variabel acak dan nilai yang diperoleh (juga dikenal sebagai pengamatan atau hasil) adalah sebagai berikut:

• Huruf kapital, seperti X, Y, atau Z, digunakan untuk mewakili variabel acak. Variabel acak adalah fungsi yang menghubungkan hasil dari suatu eksperimen acak dengan bilangan riil. Huruf kapital digunakan karena variabel acak adalah representasi abstrak dari hasil yang mungkin dari suatu proses acak.
• Huruf kecil, seperti x, y, atau z, digunakan untuk mewakili nilai yang diperoleh, pengamatan, atau hasil khusus dari variabel acak yang sesuai. Huruf kecil menunjukkan nilai konkret yang dapat diambil oleh variabel acak.

Misalnya, jika X adalah variabel acak yang mewakili hasil dari lemparan dadu, maka x akan mewakili hasil yang spesifik, seperti dadu yang menghasilkan angka 4. Ketika membahas sifat atau fungsi dari variabel acak, seperti distribusi probabilitas atau ekspektasi, huruf kapital biasanya digunakan. Sebaliknya, ketika membahas nilai spesifik, peluang, atau hasil, huruf kecil digunakan.

Distribusi Probabilitas Diskrit

Distribusi probabilitas diskrit menggambarkan variabel acak diskrit yang mengambil himpunan nilai terbatas atau terhitung tak terbatas dari nilai yang berbeda. Beberapa distribusi probabilitas diskrit yang umum meliputi:

• Distribusi Uniform
  Memberikan probabilitas yang sama untuk semua nilai yang mungkin dari variabel acak diskrit. Sering digunakan untuk memodelkan situasi di mana setiap hasil memiliki peluang yang sama untuk terjadi.

• Distribusi Bernoulli
  Menggambarkan hasil biner, seperti sukses atau kegagalan, dengan probabilitas sukses yang tetap. Berguna untuk memodelkan satu percobaan ya-tidak.

• Distribusi Binomial
  Memodelkan jumlah keberhasilan dalam sejumlah tetap dari percobaan Bernoulli yang independen dengan probabilitas keberhasilan yang sama. Banyak digunakan untuk memodelkan jumlah keberhasilan dalam sejumlah tetap dari percobaan.

• Distribusi Poisson
  Mewakili jumlah kejadian yang terjadi dalam selang waktu atau ruang yang tetap, dengan tingkat rata-rata yang konstan. Berlaku untuk memodelkan jumlah panggilan ke pusat panggilan atau kedatangan di halte bus.

• Distribusi Geometris
  Menggambarkan jumlah percobaan yang diperlukan untuk mencapai keberhasilan pertama dalam rangkaian percobaan Bernoulli yang independen. Berguna untuk memodelkan waktu tunggu hingga keberhasilan pertama.

• Distribusi Binomial Negatif
  Memodelkan jumlah percobaan yang diperlukan untuk mencapai jumlah keberhasilan tetap dalam percobaan Bernoulli yang independen. Cocok untuk menganalisis jumlah percobaan yang diperlukan untuk mencapai jumlah keberhasilan tertentu.

• Distribusi Hipergeometrik
  Menggambarkan jumlah keberhasilan dalam sejumlah tetap dari pengambilan acak tanpa penggantian dari populasi yang terbatas. Sering digunakan dalam situasi di mana pengambilan sampel dilakukan tanpa penggantian, seperti memilih komite dari sekelompok orang.

Fungsi Massa Peluang (PMF)

Fungsi massa peluang (PMF) adalah fungsi yang terkait dengan variabel acak diskrit yang menetapkan probabilitas untuk setiap nilai yang mungkin dalam domain variabel tersebut. PMF, biasanya ditulis sebagai P(X = x) atau p(x), harus memenuhi kondisi berikut:

• Probabilitas setiap nilai non-negatif (p(x) \geq 0 untuk semua x dalam domain X).
• Jumlah probabilitas dari semua nilai yang mungkin sama dengan satu (\sum p(x) = 1).

PMF digunakan untuk menggambarkan berbagai distribusi probabilitas diskrit. Memahami PMF dari distribusi yang diberikan memungkinkan kita untuk menghitung peluang, ekspektasi, dan kuantitas lain yang menarik terkait dengan variabel acak.

Distribusi Probabilitas Kontinu

Distribusi probabilitas kontinu menggambarkan variabel acak yang dapat mengambil nilai apa pun dalam rentang atau interval yang kontinu. Beberapa distribusi probabilitas kontinu yang umum meliputi:

• Distribusi Uniform
  Memberikan kepadatan probabilitas yang sama untuk semua nilai dalam interval tertentu. Sering digunakan untuk memodelkan variabel acak dengan kepadatan probabilitas konstan dalam rentang yang diberikan.

• Distribusi Normal
  Distribusi berbentuk lonceng yang dicirikan oleh mean dan deviasi standar, yang menentukan lokasi dan penyebarannya masing-masing. Banyak digunakan dalam statistik karena Teorema Pusat Batas dan prevalensinya dalam banyak fenomena alam.

• Distribusi Eksponensial
  Menggambarkan waktu antara kejadian dalam proses Poisson, di mana kejadian terjadi secara terus-menerus dan independen pada tingkat rata-rata yang konstan. Berguna untuk memodelkan waktu tunggu atau umur komponen.

• Distribusi Gamma
  Distribusi yang fleksibel yang dapat mengambil bentuk yang berbeda dan sering digunakan untuk memodelkan waktu tunggu, umur, atau variabel acak kontinu lain yang positif dengan distribusi yang condong.

• Distribusi Beta
  Memodelkan variabel acak yang terbatas pada interval tetap, biasanya [0, 1], dan dapat mengambil bentuk yang berbeda. Berguna untuk memodelkan peluang, proporsi, atau kuantitas lain yang terbatas oleh rentang yang terbatas.

• Distribusi Weibull
  Digunakan untuk memodelkan waktu umur atau kegagalan komponen, terutama dalam rekayasa keandalan dan analisis kelangsungan hidup, karena fleksibilitasnya dalam merepresentasikan berbagai perilaku tingkat kegagalan.

• Distribusi Log-normal
  Menggambarkan variabel acak yang logaritmenya mengikuti distribusi normal. Sering digunakan untuk memodelkan variabel yang positif dan memiliki distribusi yang condong ke kanan, seperti pendapatan atau harga saham.

Fungsi Kepadatan Peluang (PDF)

Fungsi kepadatan peluang (PDF) adalah fungsi yang terkait dengan variabel acak kontinu yang menentukan peluang variabel mengambil nilai dalam interval tertentu. PDF, biasanya ditulis sebagai f(x), harus memenuhi kondisi berikut:

• Kepadatan probabilitas non-negatif untuk semua nilai (f(x) \geq 0 untuk semua x dalam domain X).
• Integral fungsi kepadatan seluruh domain sama dengan satu (\int f(x) dx = 1).

PDF digunakan untuk menggambarkan berbagai distribusi probabilitas kontinu. Memahami PDF dari distribusi yang diberikan memungkinkan kita untuk menghitung peluang, ekspektasi, dan kuantitas lain yang menarik terkait dengan variabel acak dengan mengintegrasikan fungsi kepadatan di atas rentang yang diinginkan.

Fungsi Distribusi Kumulatif (CDF)

Fungsi distribusi kumulatif (CDF) adalah fungsi yang terkait dengan variabel acak diskrit dan kontinu yang mewakili probabilitas variabel acak mengambil nilai kurang dari atau sama dengan nilai x yang diberikan. CDF, biasanya ditulis sebagai F(x), didefinisikan sebagai:

CDF memiliki properti berikut:

• CDF adalah fungsi monotonik tak turun, yaitu F(x) \leq F(y) untuk x \leq y.
• CDF kontinu dari kanan, artinya untuk setiap nilai x, batas dari F(x) saat x mendekati dari kanan sama dengan F(x).
• Batas dari F(x) saat x mendekati negatif tak terhingga adalah 0, dan batas saat x mendekati positif tak terhingga adalah 1.

CDF berguna untuk menghitung peluang interval dan persentil dari variabel acak. Diberikan CDF, kita dapat menemukan peluang bahwa variabel acak berada dalam rentang tertentu dengan mengambil selisih antara nilai CDF pada titik ujung rentang. Selain itu, CDF dapat digunakan untuk menghitung kuantil dan persentil, yaitu nilai yang membagi distribusi menjadi wilayah probabilitas yang sama.

Kuantil dan Persentil

Kuantil dan persentil adalah nilai yang membagi distribusi variabel acak menjadi wilayah probabilitas yang sama. Kuantil ke-p (atau persentil ke-p ketika diekspresikan sebagai persentase) dari variabel acak X adalah nilai x_p sehingga P(X \leq x_p) = p. Kuantil dan persentil dapat dihitung menggunakan invers CDF, yang ditulis sebagai F^{-1}(p), dengan menyelesaikan untuk x_p:

Kuantil dan persentil memiliki berbagai aplikasi dalam statistik, seperti merangkum distribusi dataset, mengevaluasi kinerja model, atau mengestimasi interval kepercayaan untuk parameter.

Hubungan antara PMF, PDF, dan CDF

Untuk variabel acak diskrit, CDF dapat diperoleh dengan menjumlahkan probabilitas PMF untuk semua nilai kurang dari atau sama dengan x:

Untuk variabel acak kontinu, CDF dapat diperoleh dengan mengintegrasikan PDF dari negatif tak terhingga hingga nilai yang diberikan x:

Dalam kasus variabel acak kontinu, PDF dapat diperoleh dari CDF dengan mengambil turunan CDF terhadap x:

Menampilkan PMF, PDF, dan CDF

Pada bab ini, saya akan menggunakan Python untuk menampilkan PMF, PDF, dan CDF dari berbagai distribusi probabilitas untuk pemahaman visual. Kita akan menggunakan distribusi normal untuk PDF dan distribusi Poisson untuk PMF. Kita akan menampilkan CDF untuk kedua distribusi tersebut.

Pertama, mari impor perpustakaan yang dibutuhkan:

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from scipy.stats import norm, poisson

Sekarang, mari tentukan parameter untuk distribusi normal dan Poisson:

mu_normal = 0      # mean for normal distribution
sigma = 1          # standard deviation for normal distribution
lambda_poisson = 4 # lambda parameter for Poisson distribution

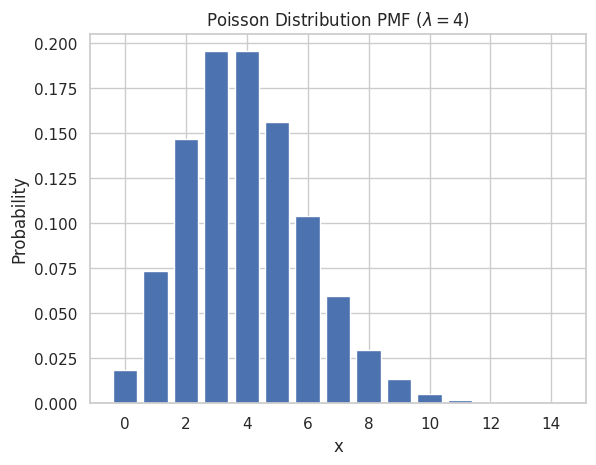
Menampilkan PMF untuk Distribusi Poisson

Untuk menampilkan PMF dari distribusi Poisson, kita dapat mengikuti langkah-langkah berikut:

1. Tentukan rentang nilai yang mungkin untuk distribusi Poisson.
2. Hitung probabilitas untuk setiap nilai menggunakan rumus PMF atau fungsi bawaan (misalnya, poisson.pmf dari scipy.stats).
3. Tampilkan probabilitas tersebut menggunakan diagram batang.

x_poisson = np.arange(0, 15)
y_poisson = poisson.pmf(x_poisson, lambda_poisson)

sns.set(style="whitegrid")
plt.bar(x_poisson, y_poisson)
plt.title("Poisson Distribution PMF ($\lambda = 4$)")
plt.xlabel("x")
plt.ylabel("Probability")
plt.show()

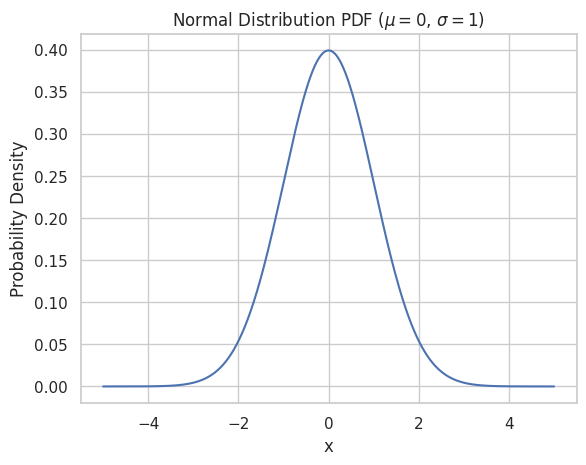
Menampilkan PDF untuk Distribusi Normal

Untuk menampilkan PDF dari distribusi normal, kita dapat mengikuti langkah-langkah berikut:

1. Buat larik titik yang sama jaraknya (misalnya, menggunakan np.linspace) yang mencakup rentang yang diinginkan dari distribusi.
2. Hitung kerapatan probabilitas untuk setiap titik menggunakan rumus PDF atau fungsi bawaan (misalnya, norm.pdf dari scipy.stats).
3. Tampilkan kerapatan tersebut menggunakan diagram garis.

x_normal = np.linspace(-5, 5, 1000)
y_normal = norm.pdf(x_normal, mu_normal, sigma)

sns.set(style="whitegrid")
plt.plot(x_normal, y_normal)
plt.title("Normal Distribution PDF ($\mu = 0$, $\sigma = 1$)")
plt.xlabel("x")
plt.ylabel("Probability Density")
plt.show()

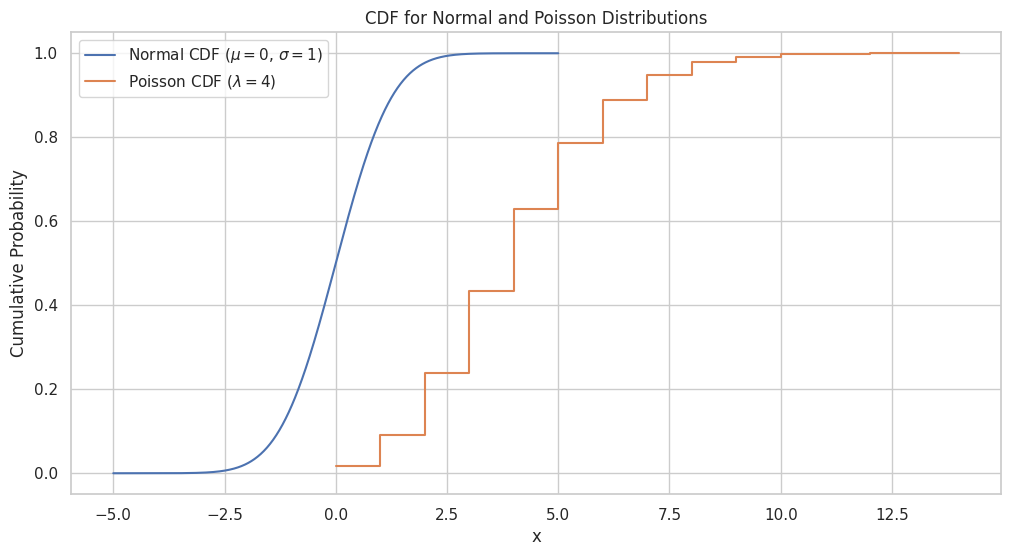
Menampilkan CDF untuk Distribusi Normal dan Poisson

Untuk menampilkan CDF dari distribusi normal dan Poisson, kita dapat mengikuti langkah-langkah berikut:

1. Buat larik titik yang sama jaraknya (misalnya, menggunakan np.linspace) yang mencakup rentang yang diinginkan dari distribusi.
2. Hitung probabilitas kumulatif untuk setiap titik menggunakan rumus CDF atau fungsi bawaan (misalnya, norm.cdf dan poisson.cdf dari scipy.stats).
3. Tampilkan probabilitas kumulatif tersebut menggunakan diagram garis.

x_normal_cdf = np.linspace(-5, 5, 1000)
y_normal_cdf = norm.cdf(x_normal_cdf, mu_normal, sigma)

x_poisson_cdf = np.arange(0, 15)
y_poisson_cdf = poisson.cdf(x_poisson_cdf, lambda_poisson)

plt.figure(figsize=(12, 6))

sns.set(style="whitegrid")
plt.plot(x_normal_cdf, y_normal_cdf, label="Normal CDF ($\mu = 0$, $\sigma = 1$)")
plt.step(x_poisson_cdf,y_poisson_cdf, label="Poisson CDF ($\lambda = 4$)", where='post')
plt.title("CDF for Normal and Poisson Distributions")
plt.xlabel("x")
plt.ylabel("Cumulative Probability")
plt.legend(loc="upper left")
plt.show()