Apa itu Distribusi normal

Distribusi normal (distribusi Gaussian) adalah salah satu distribusi probabilitas yang paling banyak digunakan secara universal dan digunakan untuk menggambarkan fenomena alam dan sosial. Distribusi normal memiliki sifat-sifat dasar berikut ini:

• Mean, median, dan modus konsisten.
• Kurva simetris dengan nilai rata-rata sebagai puncak dan nilai rata-rata sebagai pusat.
• Deviasi standar mengubah puncak kurva dan lebar distribusi.
• Sumbu x adalah asimptot.
• Area yang dibatasi oleh kurva dan sumbu x adalah 1

Contoh distribusi normal adalah tinggi badan laki-laki dewasa (perempuan).

Fungsi kepadatan probabilitas (PDF)

Ketika variabel acak univariat X mengikuti distribusi normal dengan mean \mu dan varians \sigma^2, fungsi kepadatan probabilitasnya (RDF) dinyatakan dengan

Distribusi normal dinyatakan sebagai berikut N(\mu, \sigma^2) ketika mengikuti mean \mu dan varians \sigma^2. Juga, jumlah fungsi kepadatan probabilitas dari distribusi normal adalah 1. Dengan kata lain, mengintegrasikan fungsi kepadatan probabilitas ini di seluruh interval menghasilkan 1.

Cara menurunkan fungsi kepadatan probabilitas

Sebagian besar fenomena di dunia memiliki puncak pada nilai rata-rata, dan probabilitas kejadian menurun ketika seseorang menjauh dari nilai rata-rata. Fenomena-fenomena ini dapat dinyatakan dengan fungsi berikut ini.

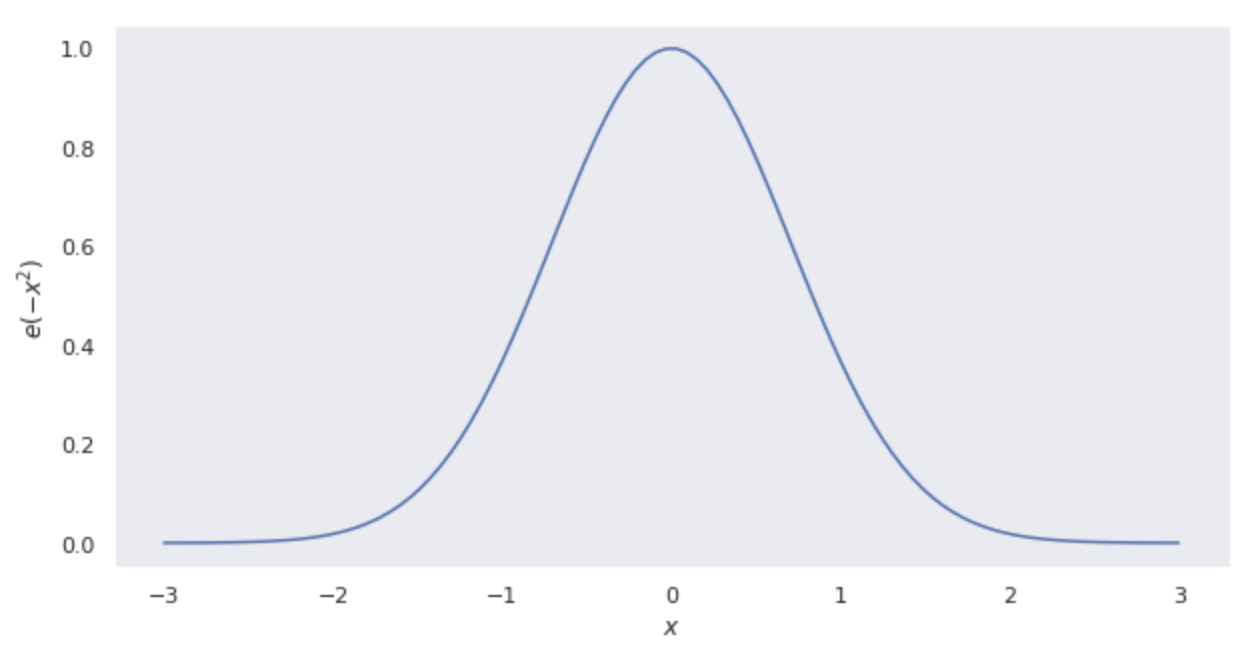
Kita akan memodifikasi fungsi di atas menjadi fungsi yang lebih umum berdasarkan hal di atas. Pertama, kita akan memungkinkan untuk menetapkan nilai rata-rata yang sewenang-wenang. Kita dapat menerjemahkan nilai mean ke kiri atau kanan tergantung pada nilai \mu sebagai berikut.

Selanjutnya, untuk memungkinkan lebar distribusi ditetapkan secara sewenang-wenang, kita mentransformasikan rumus menjadi sebagai berikut:

Lebar distribusi sekarang dapat dikontrol oleh nilai \sigma. Di sini, \sigma^2 dalam 2\sigma^2 dikuadratkan sehingga selalu bernilai positif terlepas dari nilai \sigma. Koefisien 2 ditambahkan untuk menyederhanakan hasil pengintegrasian selanjutnya.

Fungsi densitas adalah jumlah integral atas semua interval. Oleh karena itu, konstanta c ditambahkan ke awal persamaan untuk menyesuaikannya.

Menghitung persamaan di atas, konstanta c mengambil nilai berikut:

Dengan demikian, fungsi densitas probabilitas dari distribusi normal adalah persamaan berikut ini:

Probabilitas dari distribusi normal

Untuk distribusi normal, jika kita mengetahui rata-rata \mu dan deviasi standar \sigma, kita mengetahui probabilitas terjadinya variabel acak X.

Grafik distribusi normal di bawah ini menunjukkan kisaran deviasi standar (± \sigma, ±1.96 \sigma, ±2 \sigma).

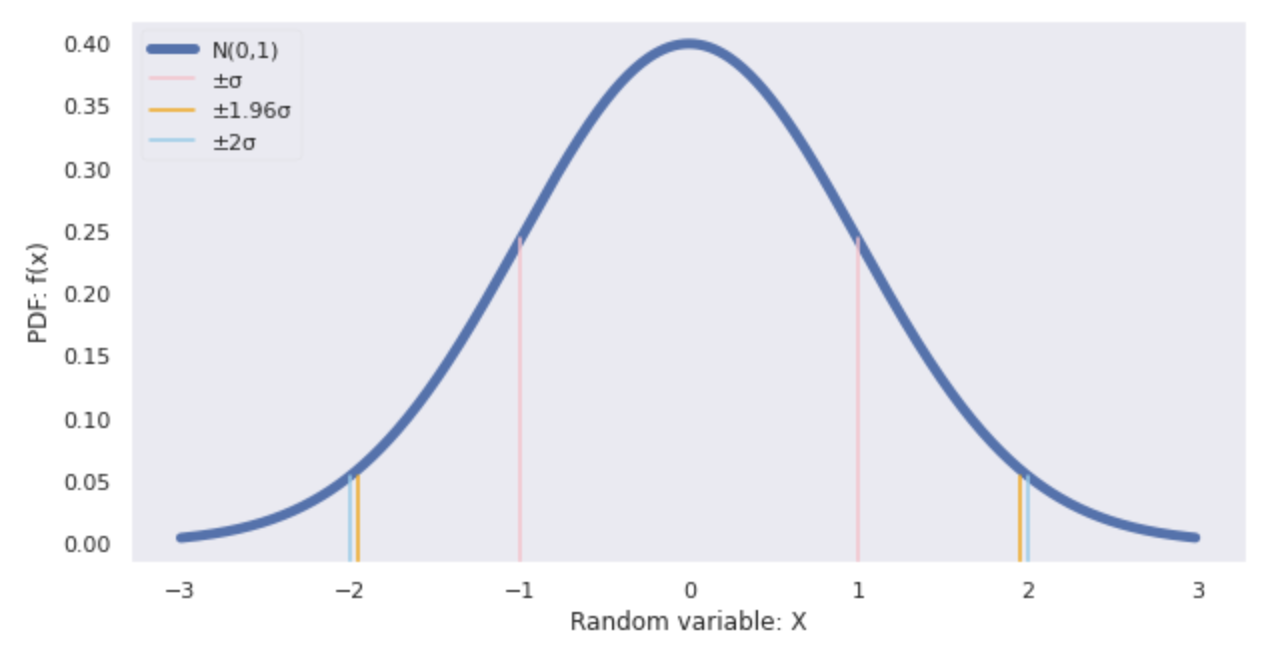
Rentang variabel acak X dan probabilitas kemunculannya adalah sebagai berikut.

Yang umum digunakan 1.96 \sigma dalam hypothesis-testing diperlakukan sebagai tingkat signifikansi 95%.

Distribusi normal standar

Ketika variabel acak X mengikuti distribusi normal N(\mu,\sigma^2), aX+b mengikuti distribusi normal N(a\mu+b,a^2\sigma^2).

Dengan menggunakan properti ini dan mentransformasikan Z=X-\mu\sigma, Z mengikuti distribusi normal dengan mean 0 dan varians 1. Transformasi ini disebut standardisasi distribusi normal, dan distribusi normal dengan mean 0 dan varians 1 disebut distribusi normal standar.

Sifat reproduksi dari distribusi normal

Properti reproduksi distribusi normal berarti bahwa ketika variabel acak X dan Y secara independen mengikuti distribusi normal N(\mu_1,\sigma^2_1) dan N(\mu_2,\sigma^2_2) masing-masing, distribusi X+Y adalah distribusi normal Properti bahwa N(\mu_1+\mu_2,\sigma^2_1+\sigma^2_2).

Sebagai contoh, asumsikan bahwa variabel acak yang saling independen X dan Y masing-masing mengikuti N(2, 2^2) dan N(5, 3^2), dan temukan distribusi probabilitas yang diikuti oleh variabel acak 3X + 2Y.

Distribusi probabilitas yang diikuti oleh variabel acak 3X adalah sebagai berikut:

Distribusi probabilitas yang diikuti oleh variabel acak 2Y adalah sebagai berikut:

Dari properti reproduksi distribusi normal, distribusi probabilitas yang diikuti oleh variabel acak 3X + 2Y adalah

Distribusi probabilitas yang diikuti oleh variabel acak 3X + 2Y adalah distribusi normal dengan nilai ekspektasi 16 dan varians 72.

Kode Python

Kode Python yang digunakan dalam artikel ini adalah sebagai berikut.

Gambarkan y=e^{-x^2}

```python
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from matplotlib import rcParams
rcParams['figure.figsize'] = 10, 5
# %matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

x = np.linspace(-3, 3, 100)
y = np.exp(x)

plt.figure()
plt.plot(x, np.exp(-x**2))
plt.xlabel('$x$')
plt.ylabel('$-\exp(-x^2)$')

plt.show()

Gambarkan distribusi normal

from scipy import stats
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
from matplotlib import rcParams
rcParams['figure.figsize'] = 10, 5
# %matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

# normal distribution setting
mean = 0
std  = 1

# set random variable
X = np.arange(-3,3,0.01)

# calculate PDF
Y = stats.norm.pdf(X,mean,std)

# draw normal distribution
plt.plot(X,Y,label="N(0,1)", linewidth=5)

# draw standard deviation
plt.axvline(x=std, color="pink", ymax=1.5*Y.max(), label="±σ")
plt.axvline(x=-std, color="pink", ymax=1.5*Y.max())
plt.axvline(x=1.96*std, color="orange", ymax=0.4*Y.max(), label="±1.96σ")
plt.axvline(x=-1.96*std, color="orange", ymax=0.4*Y.max())
plt.axvline(x=2*std, color="skyblue", ymax=0.4*Y.max(), label="±2σ")
plt.axvline(x=-2*std, color="skyblue", ymax=0.4*Y.max())

# graph setting
plt.xlabel("Random variable: X")
plt.ylabel("PDF: f(x)")
plt.legend(loc="upper left")
plt.show()