Apa itu distribusi geometris

Distribusi geometris adalah distribusi probabilitas yang mengikuti probabilitas p dari suatu peristiwa yang terjadi beberapa kali sampai peristiwa itu terjadi. Distribusi geometris digunakan dalam contoh berikut.

• Berapa kali sebuah koin dilempar sampai bagian depan muncul
• Jumlah tembakan yang dilakukan pemain basket dengan tingkat keberhasilan tiga poin 30% sebelum melakukan tembakan tiga angka

Ketika variabel acak X mengikuti distribusi geometris, probabilitas suatu peristiwa terjadi untuk pertama kalinya pada waktu ke-k dalam percobaan dengan probabilitas kejadian p dinyatakan sebagai berikut:

Distribusi geometris kadang-kadang dilambangkan sebagai X \sim Geo(p).

Untuk p = 0.05, 0.1, dan 0.5, distribusi geometrisnya adalah sebagai berikut.

Misalnya, probabilitas bahwa lemparan ketiga dari sebuah koin akan menghasilkan sebuah wajah untuk pertama kalinya dapat ditentukan sebagai berikut:

Kita menemukan bahwa probabilitas tabel muncul untuk pertama kalinya pada lemparan ketiga adalah 12,5%.

Hubungan dengan distribusi binomial

Distribusi binomial adalah distribusi probabilitas yang mengikuti berapa kali suatu peristiwa terjadi ketika p adalah probabilitas terjadinya suatu peristiwa dan n pengamatan terhadap peristiwa tersebut dilakukan. Distribusi geometris, di sisi lain, adalah distribusi probabilitas yang mengikuti berapa kali suatu peristiwa terjadi ketika p adalah probabilitas terjadinya peristiwa tersebut.

Dengan kata lain, distribusi binomial mempertimbangkan peristiwa yang sama dalam hal "berapa kali" sedangkan distribusi geometris mempertimbangkannya dalam hal "waktu/interval".

Kita juga dapat mengatakan bahwa distribusi geometris adalah nilai n ketika X_1=X_2=... =X_{n-1}=0, X_n=1 dalam variabel acak X_1,X_2,..., yang mengikuti distribusi Bernoulli dengan probabilitas p.

Nilai yang diharapkan dan varians dari distribusi geometris

Ketika variabel acak X mengikuti distribusi geometris dengan probabilitas keberhasilan p, nilai dan varians yang diharapkan adalah sebagai berikut:

Memoryless dari distribusi geometris

Jika variabel acak X mengikuti distribusi geometris dan m, n > 0, maka persamaan berikut berlaku.

Persamaan di atas mengimplikasikan bahwa waktu sampai terjadinya peristiwa di masa depan tidak bergantung pada keberadaan peristiwa masa lalu itu. Sebagai contoh, jika sebuah koin dilempar tiga kali, dan dua lemparan pertama semuanya benar, hasilnya tidak mempengaruhi probabilitas lemparan ketiga yang benar sama sekali. Sifat ini disebut memoryless. Distribusi geometris adalah satu-satunya distribusi diskrit dengan memoryless.

Kode Python

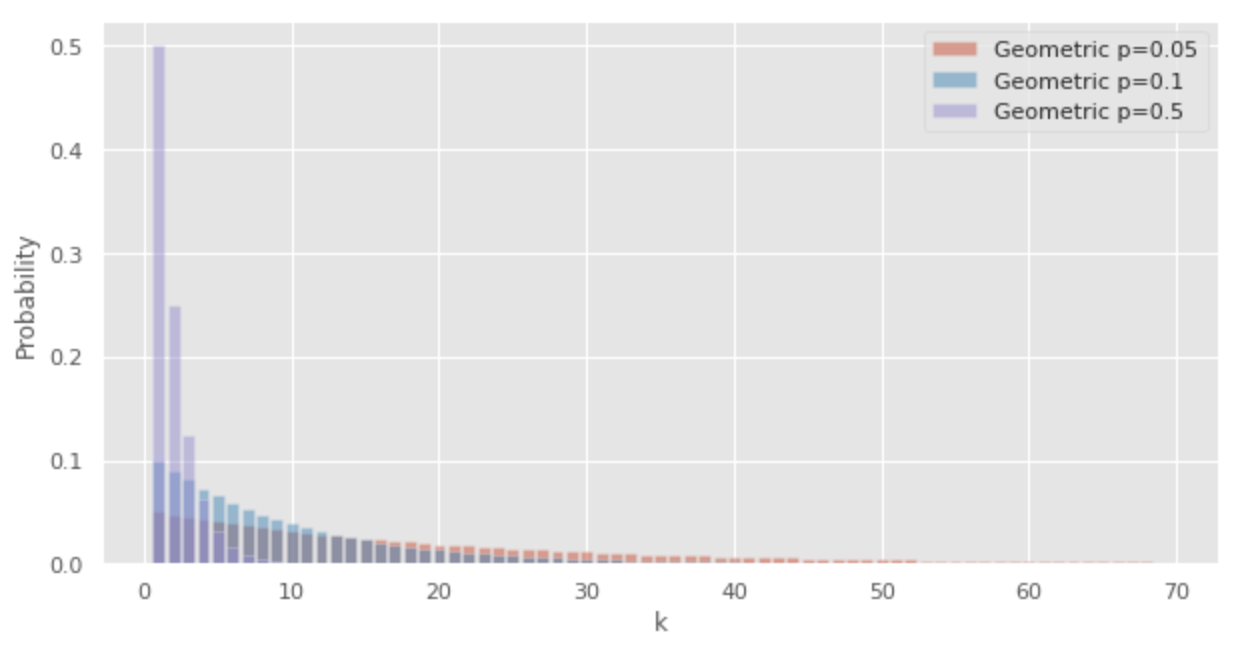
Kode Python berikut dapat digunakan untuk menggambar distribusi geometris.

import numpy as np
from scipy.stats import geom
import matplotlib.pyplot as plt

x =  np.arange(1, 70, 1)

# probability of the geometric distribution
y005= [geom.pmf(i, 0.05) for i in x]
y01= [geom.pmf(i, 0.1) for i in x]
y05= [geom.pmf(i, 0.5) for i in x]

# draw graph
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

ax.bar(x,y005,alpha=0.5, label="Geometric p=0.05")
ax.bar(x,y01,alpha=0.5, label="Geometric p=0.1")
ax.bar(x,y05,alpha=0.5, label="Geometric p=0.5")

ax.legend()
ax.set_xlabel("k")
ax.set_ylabel("Probability")
plt.show()