2022-11-18

Pengujian Hipotesis

Apa itu Pengujian Hipotesis

Pengujian Hipotesis adalah metode estimasi statistik di mana hipotesis dirumuskan untuk populasi dan sampel digunakan untuk menguji kebenaran atau kepalsuan hipotesis secara statistik. Dalam pengujian hipotesis, Hipotesis alternatif diasumsikan dan Hipotesis nol diasumsikan sebagai hipotesis yang tidak sesuai dengan klaim itu, dan ketika hipotesis nol ditolak, atau dengan kata lain, dinegasikan, hipotesis alternatif dianggap benar dengan cara yang rasional kembali.

Prosedur Pengujian Hipotesis

Pengujian hipotesis dilakukan menurut prosedur berikut ini:

Merumuskan hipotesis nol dan alternatif
Hitung statistik uji (pemilihan uji)
Tetapkan tingkat signifikansi α (menetapkan wilayah penolakan)
Tolak atau terima hipotesis nol

Merumuskan Hipotesis Nol dan Alternatif

Nyatakan hipotesis secara statistik sehingga probabilitas bahwa sampel akan diamati dengan asumsi hipotesis benar dapat dihitung. Tes ini merupakan pilihan antara dua pilihan berikut, dan tujuannya adalah untuk menguji apakah hipotesis nol dapat ditolak.

Hipotesis nol
Hipotesis nol adalah hipotesis yang dapat dirumuskan untuk menentukan apakah itu benar atau tidak. Hipotesis nol kemudian diuji dan ditarik kesimpulan. Hipotesis nol ditulis sebagai $H_0$ .
Hipotesis alternatif
Hipotesis alternatif adalah hipotesis yang menentang hipotesis nol dan diadopsi ketika hipotesis nol ditolak. Hipotesis alternatif adalah hipotesis yang semula ingin kita buktikan. Hipotesis alternatif ditulis sebagai $H_1$ .

Sebagai contoh, jika kita ingin menguji apakah efek suatu obat dapat diklaim secara signifikan, hipotesis nol dan alternatif masing-masing ditetapkan sebagai berikut.

Hipotesis nol ( $H_0$ ): Efek obat tidak dapat diklaim.
Hipotesis alternatif ( $H_1$ ): Efek obat dapat diklaim.

Di sini, karena pengujian hipotesis adalah tes yang menolak hipotesis nol dan bertujuan untuk membuktikan kebenaran dari apa yang ingin Anda klaim, Anda harus selalu menetapkan hipotesis yang ingin Anda klaim sebagai hipotesis alternatif dan hipotesis yang tidak ingin Anda klaim sebagai hipotesis nol.

Ada dua alasan mengapa uji hipotesis mengambil pendekatan untuk menjelaskan kebenaran hipotesis (hipotesis alternatif) dengan menolak hipotesis nol.

Kadang-kadang sulit untuk membuktikan secara langsung hipotesis alternatif.
Untuk menghindari pemilihan hipotesis alternatif yang ceroboh.

Untuk alasan pertama, hipotesis alternatif mungkin tidak dapat dihitung probabilitasnya. Sebagai contoh, jika kita menduga bahwa probabilitas dua sisi koin tidak 1/2, hipotesis nol dan hipotesis alternatif adalah sebagai berikut

Hipotesis nol ( $H_0$ ): Probabilitas dua sisi koin adalah 1/2.
Hipotesis alternatif ( $H_1$ ): Probabilitas dua sisi koin tidak 1/2.

Di sini, untuk menghitung probabilitas dua sisi koin, setelah probabilitas ditetapkan menjadi 1/2, yaitu, hipotesis nol harus diasumsikan benar, jika tidak, probabilitas tidak dapat dihitung. Jadi, prosesnya adalah mengasumsikan bahwa hipotesis nol benar, yang memungkinkan kita untuk menghitung probabilitas, dan kemudian secara statistik menolak hipotesis nol untuk membuktikan hipotesis alternatif.

Untuk alasan kedua, tes ini memiliki dua kesalahan α error dan β error.

	Hipotesis alternatif benar	Hipotesis nol benar
Tolak hipotesis nol	α error	OK
Terima hipotesis nol	OK	β error

Apakah α error atau β error adalah kesalahan yang lebih penting tergantung pada kasusnya.

Dalam kasus β error, paling tidak kesimpulannya tetap dipertahankan. Gagasan pengujian hipotesis adalah untuk menghindari dengan mudah mengadopsi hipotesis alternatif dengan menetapkan tingkat signifikansi yang ketat untuk membuat α error lebih kecil kemungkinannya terjadi.

Hitung Statistik Uji (Pemilihan Uji)

Statistik uji adalah statistik yang dihitung dari sampel menurut aturan tertentu untuk pengujian hipotesis. Metode penghitungan statistik uji tergantung pada distribusi populasi dan faktor lainnya.

Statistik uji yang umum termasuk uji T, uji F, uji Z, dan uji Chi-square.

Nama uji	Statistik uji	Tujuan
Uji T	Nilai t	Apakah rata-rata dua populasi berbeda secara signifikan atau tidak
Uji F	Nilai f	Apakah deviasi standar dari kedua populasi berbeda secara signifikan atau tidak
Uji Z	Nilai z	Apakah rata-rata sampel dan rata-rata populasi secara statistik berbeda secara signifikan atau tidak
Uji Chi-square	Nilai Chi-square	Apakah dua pengamatan untuk dua variabel saling bebas satu sama lain (independensi) dan apakah distribusi frekuensi yang diamati sama dengan distribusi teoritis (goodness of fit)

Tetapkan Tingkat Signifikansi α (Menetapkan Wilayah Penolakan)

Dengan mengasumsikan bahwa hipotesis nol benar, seluruh distribusi statistik uji dibagi menjadi Wilayah Penolakan dan Wilayah Penerimaan, dan probabilitas bahwa hipotesis nol jatuh dalam Wilayah Penolakan adalah tingkat signifikansi pengujian. Dengan kata lain, tingkat signifikansi adalah probabilitas standar untuk menentukan bahwa hipotesis nol salah. Tingkat signifikansi biasanya ditetapkan pada nilai kecil seperti 1% atau 5%.

Ketika pengujian, kesimpulannya adalah menolak hipotesis nol karena statistik uji jatuh di dalam wilayah penolakan, yaitu, peristiwa terjadi dengan cara yang jarang terjadi untuk distribusi yang sedang diuji. Ketika statistik uji jatuh dalam wilayah penolakan dan hipotesis nol ditolak, ungkapan "signifikan secara statistik" digunakan.

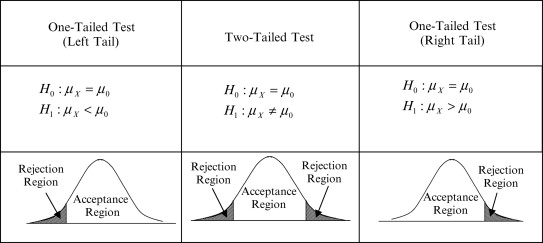
Ada uji dua ekor dan uji satu ekor seperti di bawah ini.

Rejection region
Tailed Test

Uji satu-ekor adalah metode pengujian di mana hanya probabilitas sisi kiri atau kanan yang diambil sebagai tingkat signifikansi α. Karena hanya satu sisi yang diambil sebagai tingkat signifikansi α, rentang penolakan lebih luas daripada uji dua-ekor pada tingkat signifikansi yang sama. Dengan kata lain, uji satu-ekor lebih mungkin menolak hipotesis nol daripada uji dua-ekor. Misalnya, pada tingkat signifikansi α=0,05, uji dua-ekor memiliki rentang penolakan 2,5% di setiap sisi, sedangkan uji satu sisi memiliki rentang penolakan 5% di kedua sisi.

Uji satu-ekor dilakukan dalam kasus-kasus berikut:

Ketika rata-rata sampel diketahui dengan jelas lebih besar (lebih kecil) dari nilai tertentu.
Ketika Anda ingin memeriksa hanya bahwa rata-rata sampel lebih besar (lebih kecil) dari nilai tertentu.

Tolak atau Terima Hipotesis Nol

Menentukan apakah statistik uji yang dihitung berada dalam wilayah penolakan. Biasanya, probabilitas $p$ bahwa statistik uji yang dihitung sama dengan atau lebih ekstrim dari nilai yang dihipotesiskan diperoleh dari tabel distribusi, dan nilai $p$ dibandingkan dengan α. Jika $p$ < α, hipotesis nol ditolak dan hipotesis alternatif diadopsi.

Di sisi lain, jika statistik uji berada di luar wilayah penolakan, tidak ada bukti yang cukup untuk menolak hipotesis nol, dan hipotesis nol tidak dapat ditolak dan pengujian gagal. Dengan kata lain, dalam kasus ini, kita tidak mengetahui apakah hipotesis nol atau alternatif benar. Karena uji hipotesis adalah metode untuk menolak hipotesis nol yang berlawanan untuk mengklarifikasi secara statistik klaim bahwa hipotesis alternatif adalah benar, ini bukan tes untuk membuktikan bahwa hipotesis nol benar, dan dengan demikian berakhir dengan cara ini.

Contoh Pengujian Hipotesis

Dalam hal ini, kita akan melakukan uji hipotesis untuk memverifikasi apakah berat kentang goreng di toko hamburger di depan stasiun adalah seperti nilai yang dipublikasikan yaitu 135g.

Pertama, kita pertimbangkan hipotesisnya. Dengan asumsi bahwa kita menduga bahwa berat kentang goreng tidak seperti yang dipublikasikan, hipotesis nol dan alternatifnya adalah sebagai berikut

Hipotesis nol ( $H_0$ ): Berat kentang goreng di toko hamburger di depan stasiun adalah seperti nilai yang dipublikasikan, yaitu 135g.
Hipotesis alternatif ( $H_1$ ): Berat kentang goreng di toko hamburger di depan stasiun tidak seperti nilai yang dipublikasikan yaitu 135g.

Misalkan 10 kentang goreng dibeli di toko hamburger di depan stasiun dan berat setiap kentang goreng diukur sebagai berikut:

130g
140g
124g
120g
133g
126g
131g
132g
130g
134g

Rata-rata sampel $\overline{X}$ (rata-rata dari berat 10 kentang goreng yang dibeli) adalah 130g.

Selanjutnya, kita menghitung statistik uji. Kali ini, kita asumsikan bahwa varians populasi diketahui dan $\sigma^2$ = 36. Jika varians populasi diketahui, nilai z digunakan sebagai statistik uji. Ada statistik uji lain seperti nilai-t, tetapi nilai-t digunakan dalam kasus-kasus berikut.

Varians populasi tidak diketahui
Ukuran sampel kurang dari 30

Dengan asumsi bahwa berat kentang goreng di toko hamburger di depan stasiun mengikuti distribusi normal, rata-rata sampel dari 10 kentang goreng yang dibeli (n = 10) mengikuti $N(\mu, \sigma^2 / 10)$ dengan $\mu$ untuk rata-rata populasi dan $\sigma^2$ untuk varians populasi. Dengan asumsi bahwa hipotesis nol benar, kita dapat mengasumsikan bahwa rata-rata populasi $\mu$ =135, dan statistik uji z dapat diperoleh sebagai berikut:

z = \frac{\overline{X} - \mu}{\sigma / \sqrt{n}} = \frac{130 - 135}{6 / \sqrt{10}} = -2.64

Selanjutnya, tetapkan tingkat signifikansi. Dalam hal ini, tingkat signifikansi ditetapkan ke α = 0,05, yang merupakan nilai yang paling umum. Karena kita menguji apakah berat kentang goreng adalah 135g, yang merupakan nilai yang dipublikasikan, kita mengadopsi uji dua ekor.

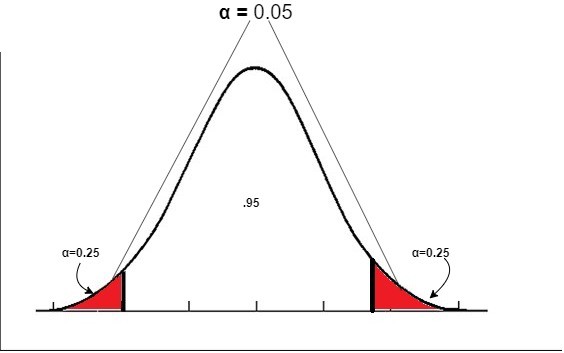
Significance level
Hypothesis Testing — 2-tailed test

Area merah pada gambar di atas adalah wilayah penolakan. Wilayah penolakan menyumbang 5% dari total, dan wilayah penolakan di kedua ujungnya masing-masing menyumbang 2,5% dari total.

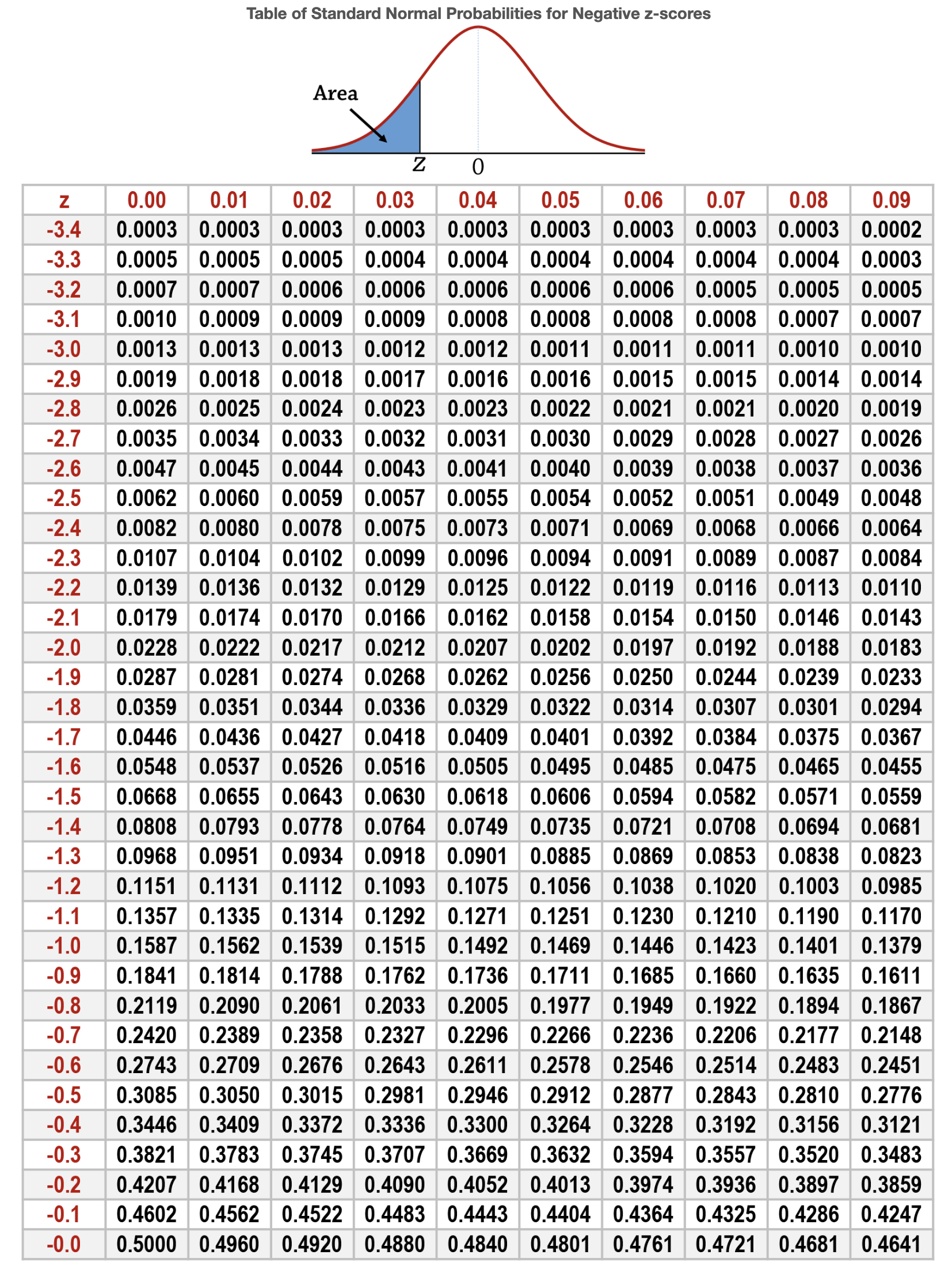
Akhirnya, nilai-p diperoleh. Karena statistik uji Z mengikuti distribusi normal standar, kita memeriksa nilai yang sesuai dengan statistik uji z = -2.64 dari tabel distribusi normal standar di bawah ini.

Standard normal distribution table
Using the Normal Distribution

Statistik uji z = -2.64 memiliki nilai 0.0041. Karena ini adalah uji dua ekor, p = 0,0082, dan p < α, kita dapat menyimpulkan bahwa sangat jarang peristiwa yang diamati terjadi di bawah hipotesis yang kita tetapkan.

Oleh karena itu, kesimpulan dari pengujian ini adalah bahwa hipotesis nol ditolak dan hipotesis alternatif diterima. Ini berarti bahwa berat kentang goreng di toko hamburger di depan stasiun bukanlah nilai yang dipublikasikan yaitu 135g.