Apa itu distribusi beta

Distribusi beta adalah distribusi probabilitas yang diikuti oleh tingkat keberhasilan $x$ dari suatu peristiwa ketika jumlah keberhasilan $\alpha$ dan kegagalan $\beta$ dari percobaan tertentu diketahui. Misalnya, jika lemparan koin diulang 10 kali dan bagian depan $\alpha$ muncul 7 kali dan bagian belakang $\beta$ muncul 3 kali, maka tingkat keberhasilan (probabilitas muncul dengan bagian depan) mengikuti distribusi beta.

Fungsi kepadatan probabilitas dari distribusi beta dinyatakan dengan persamaan berikut.

f(x) = {\frac{x^{\alpha -1}(1-x)^{\beta -1}}{B(\alpha ,\beta)}}

B(\alpha, \beta) = \int_{0}^{1}x^{\alpha-1}(1-x)^{\beta-1}dx

Distribusi beta memiliki bentuk yang fleksibel tergantung pada nilai $\alpha$ dan $\beta$ , seperti yang ditunjukkan gambar di bawah ini.

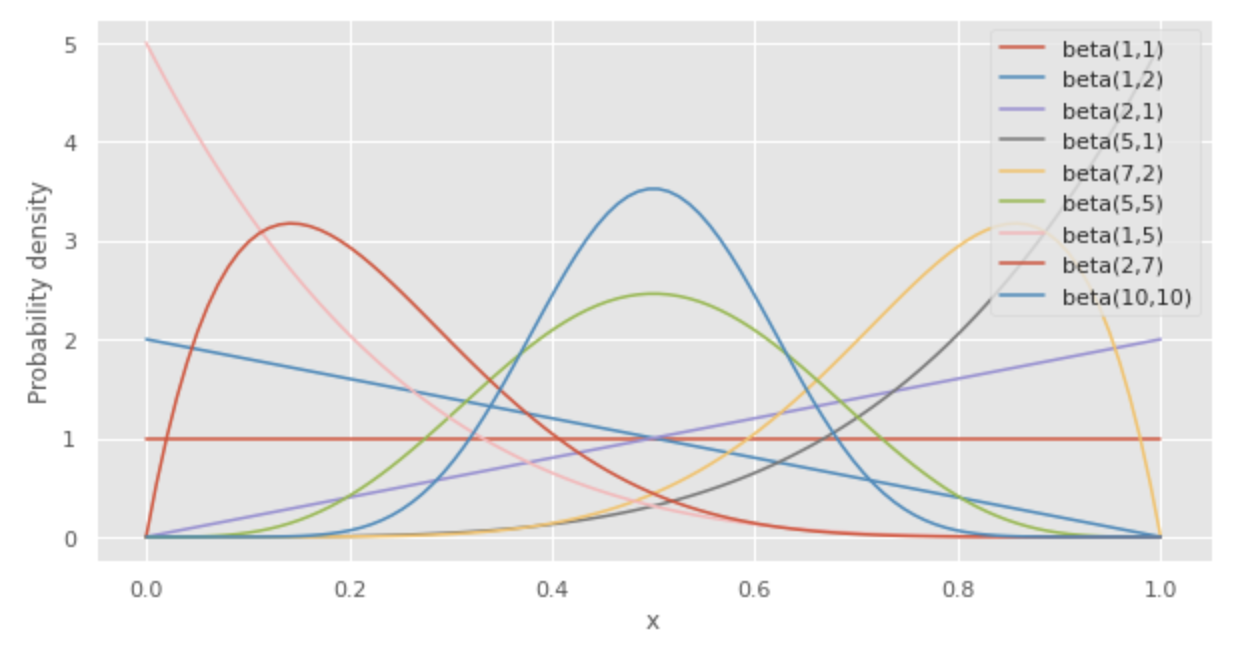
Beta distribution

Oleh karena itu, sering digunakan dalam statistik Bayesian karena mudah diperlakukan sebagai distribusi probabilitas sebelumnya.

Pengaruh α pada distribusi beta

Tergantung pada nilai $\alpha$ dalam distribusi beta, bentuk distribusinya adalah sebagai berikut.

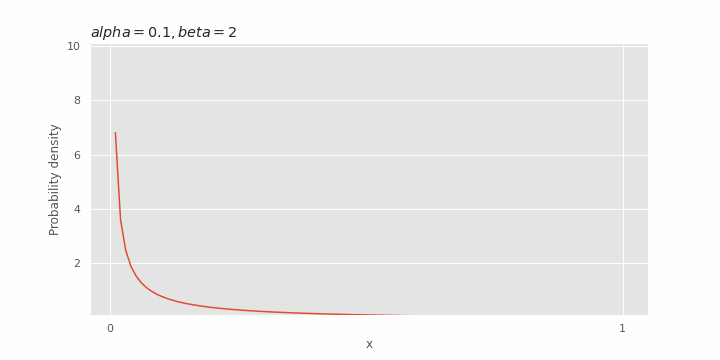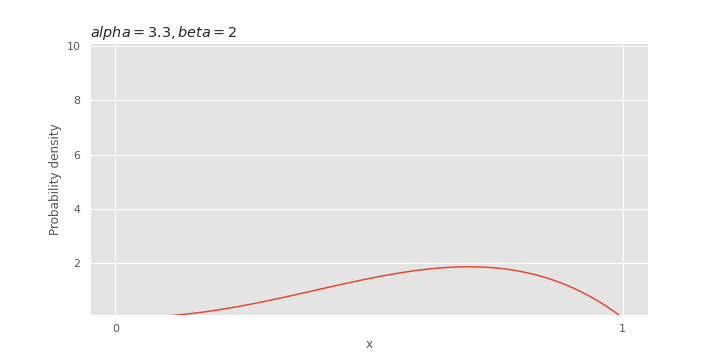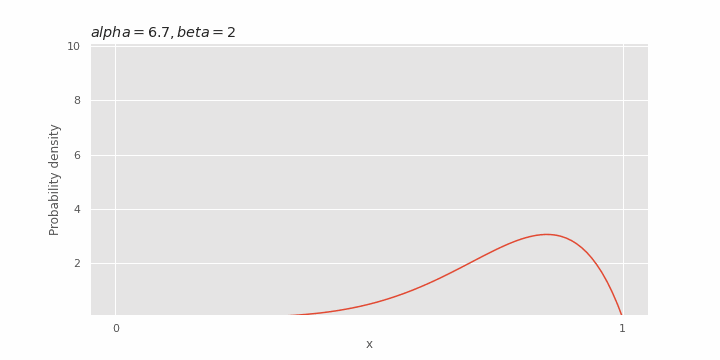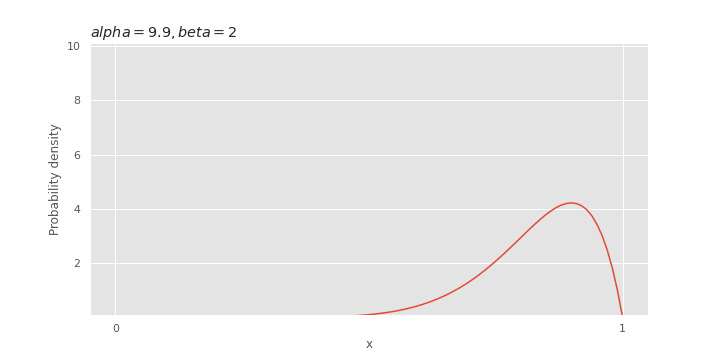
Beta distribution alpha

Pengaruh β pada distribusi beta

$\beta$ dari distribusi beta memiliki bentuk distribusi berikut tergantung pada nilainya.

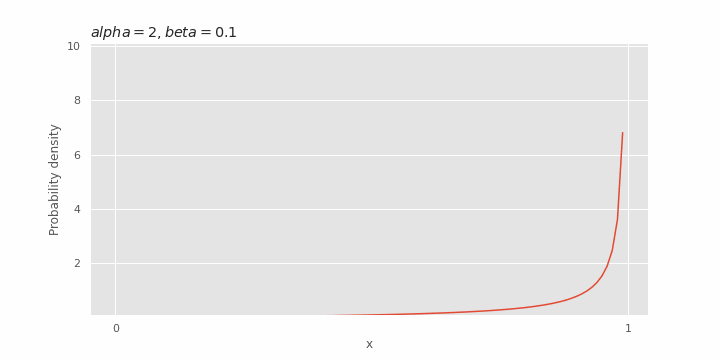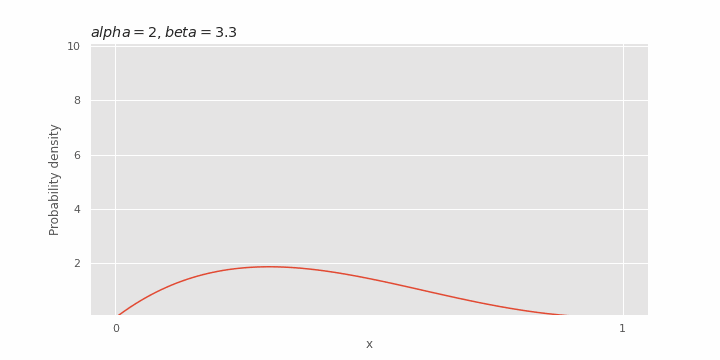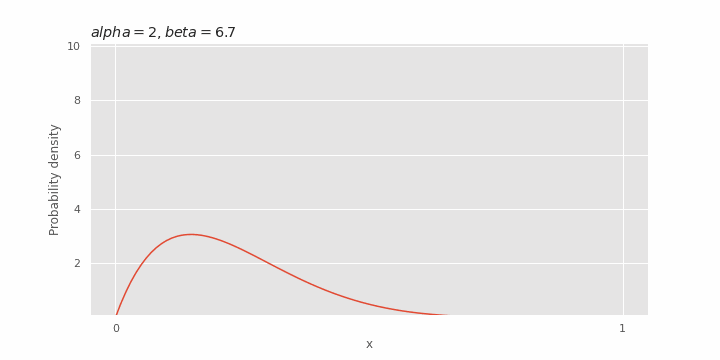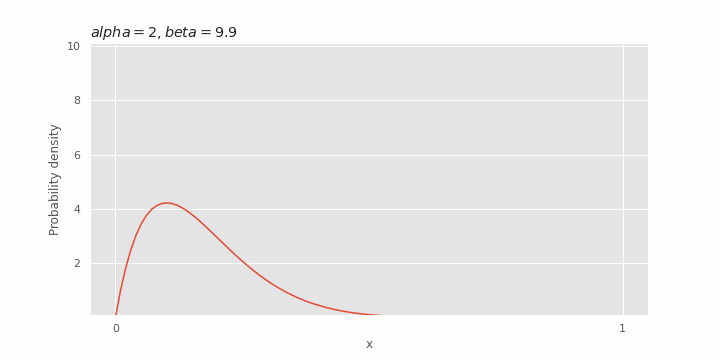
Beta distribution beta

Nilai yang diharapkan dan varians dari distribusi beta

Nilai yang diharapkan dan varians dari distribusi beta masing-masing adalah:

E(X)=\frac{\alpha}{\alpha + \beta}

V(X)=\frac{\alpha \beta}{(\alpha + \beta)^2(\alpha + \beta + 1)}

Kode Python

Kode Python yang digunakan dalam artikel ini adalah sebagai berikut.

Menggambar distribusi beta

import numpy as np
from scipy.stats import beta
import matplotlib.pyplot as plt

plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))

# x axis
x = np.linspace(0, 1, 100)

# draw graph
plt.plot(x, beta.pdf(x, 1, 1), label='beta(1,1)')
plt.plot(x, beta.pdf(x, 1, 2), label='beta(1,2)')
plt.plot(x, beta.pdf(x, 2, 1), label='beta(2,1)')
plt.plot(x, beta.pdf(x, 5, 1), label='beta(5,1)')
plt.plot(x, beta.pdf(x, 7, 2), label='beta(7,2)')
plt.plot(x, beta.pdf(x, 5, 5), label='beta(5,5)')
plt.plot(x, beta.pdf(x, 1, 5), label='beta(1,5)')
plt.plot(x, beta.pdf(x, 2, 7), label='beta(2,7)')
plt.plot(x, beta.pdf(x, 10, 10), label='beta(10,10)')
plt.legend()
plt.xlabel("x")
plt.ylabel("Probability density")
plt.show()

Beta distribution

Menggambar dampak dari α

import numpy as np
from scipy.stats import beta
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from matplotlib.animation import FuncAnimation

rc('animation', html='html5')
np.random.seed(5)

# Set up formatting for the movie files
Writer = animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)

prob_vals = np.arange(start=0.1, stop=10.01, step=0.2)

plt.style.use('ggplot')
fig = plt.figure(figsize=(10, 5))

# x axis
x = np.linspace(0, 1, 100)

def update(i):
    # initialize the graph of the previous frame
    plt.cla()
    p = prob_vals[i]

    # draw graph
    plt.plot(x, beta.pdf(x, round(p, 1), 2))
    plt.title(f'$alpha={str(round(p, 1))}, beta=2$', loc='left')
    plt.xlabel("x")
    plt.ylabel("Probability density")
    plt.ylim(0.1, 10.1)
    plt.xticks(ticks=[0, 1]) # x axis ticks

anime_prob = FuncAnimation(fig, update, frames=len(prob_vals), interval=1000)
anime_prob.save('beta_dist_alpha.gif', writer='pillow', fps=10)

Beta distribution alpha

Menggambar dampak dari β

import numpy as np
from scipy.stats import beta
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from matplotlib.animation import FuncAnimation

rc('animation', html='html5')
np.random.seed(5)

# Set up formatting for the movie files
Writer = animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)

prob_vals = np.arange(start=0.1, stop=10.01, step=0.2)

plt.style.use('ggplot')
fig = plt.figure(figsize=(10, 5))

# x axis
x = np.linspace(0, 1, 100)

def update(i):
    # initialize the graph of the previous frame
    plt.cla()
    p = prob_vals[i]

    # draw graph
    plt.plot(x, beta.pdf(x, 2, round(p, 1)))
    plt.title(f'$alpha=2, beta={str(round(p, 1))}$', loc='left')
    plt.xlabel("x")
    plt.ylabel("Probability density")
    plt.ylim(0.1, 10.1)
    plt.xticks(ticks=[0, 1]) # x axis ticks

anime_prob = FuncAnimation(fig, update, frames=len(prob_vals), interval=1000)
anime_prob.save('beta_dist_beta.gif', writer='pillow', fps=10)

Beta distribution beta

Distribusi beta