Apa itu distribusi binomial

Distribusi binomial adalah distribusi yang mengikuti probabilitas $p$ dari suatu peristiwa yang terjadi $X$ kali $n$ pengamatan dari peristiwa itu. Distribusi binomial kadang-kadang dilambangkan sebagai $B(n,p)$.

Sebagai contoh, distribusi dari berapa kali $X$ bahwa 1 ($p=\frac{1}{6}$) terjadi setelah tiga kali pelemparan dadu ($n$ = 3) mengikuti distribusi binomial.

Probabilitas distribusi binomial dinyatakan dengan persamaan berikut.

Contoh Dadu

Mari kita pertimbangkan distribusi berapa kali sebuah dadu melempar 1 sebanyak tiga kali.

Pertama, mari kita pertimbangkan kejadian-kejadiannya. Ada dua pola kejadian berikut ini.

• 1 dilempar.
• 1 tidak dilempar.

Karena ada dua pilihan kejadian atau tidak terjadi, distribusi peluang peristiwa ini adalah distribusi binomial.

Selanjutnya, mari kita pertimbangkan probabilitas kejadian yang terjadi: probabilitas mata 1 terjadi dan probabilitas mata 1 tidak terjadi masing-masing adalah sebagai berikut.

Ada empat pola berapa kali dadu akan melempar angka 1 setelah tiga kali lemparan: 0, 1, 2, dan 3 kali. Probabilitas masing-masing adalah sebagai berikut.

Deskripsi umum dari probabilitas di atas adalah persamaan probabilitas yang terdistribusi binomial berikut ini.

Memeriksa dengan Python

Mari kita periksa distribusi $B(3,\frac{1}{6})$ menggunakan Python. Kodenya adalah sebagai berikut. Ukuran sampel adalah 1.000.

from scipy.stats import binom
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

data_binom = binom.rvs(n=3, p=1/6, size=1000)
plt.figure(figsize=(10,5))
sns.distplot(data_binom, kde=False)

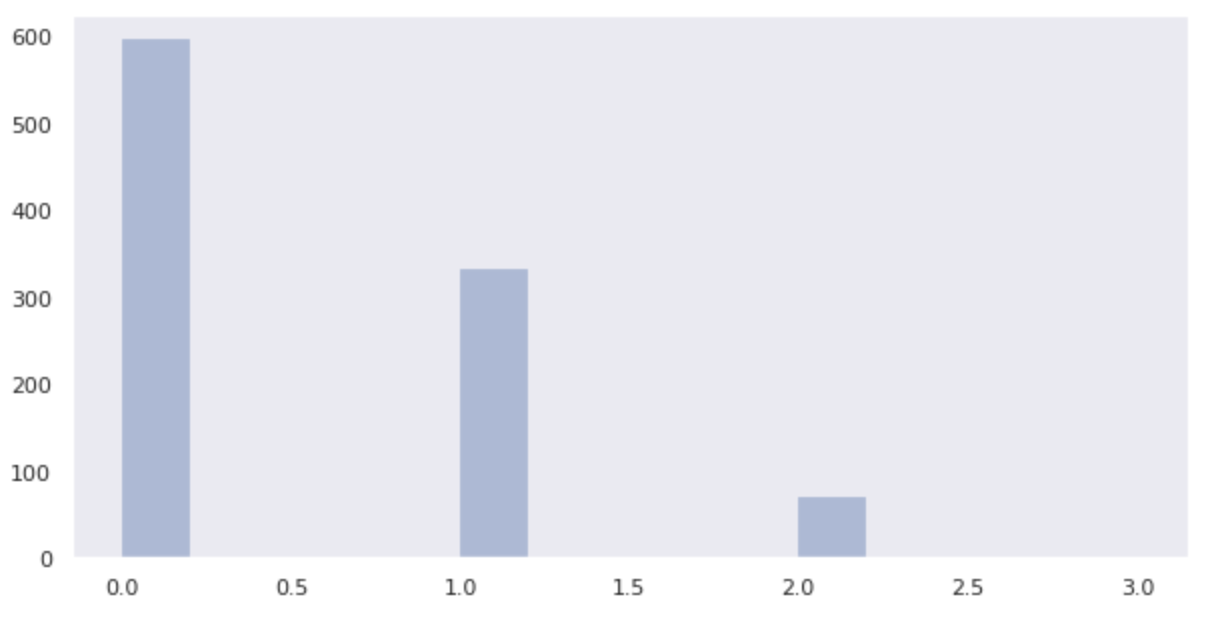
Dapat dilihat bahwa probabilitasnya mendekati nilai yang dihitung dari probabilitas berikut ini.

Teorema Laplace

Ketika variabel acak X mengikuti distribusi binomial $B(n,p)$, variabel acak tersebut mendekati distribusi normal ketika $n$ dibuat cukup besar. Ini disebut Teorema Laplace.

Mari kita periksa teorema Laplace di Python. Kali ini, kita akan memeriksa distribusi $B(100,\frac{1}{6})$ dari jumlah angka 1 yang diperoleh dengan melempar dadu sebanyak 100 kali. Ukuran sampelnya adalah 1.000.

from scipy.stats import binom
import seaborn as sns
from matplotlib import pyplot as plt
%matplotlib inline

sns.set()
sns.set_context(rc = {'patch.linewidth': 0.2})
sns.set_style('dark')

data_binom = binom.rvs(n=100, p=1/6, size=1000)
plt.figure(figsize=(10,5))
sns.distplot(data_binom, kde=False)

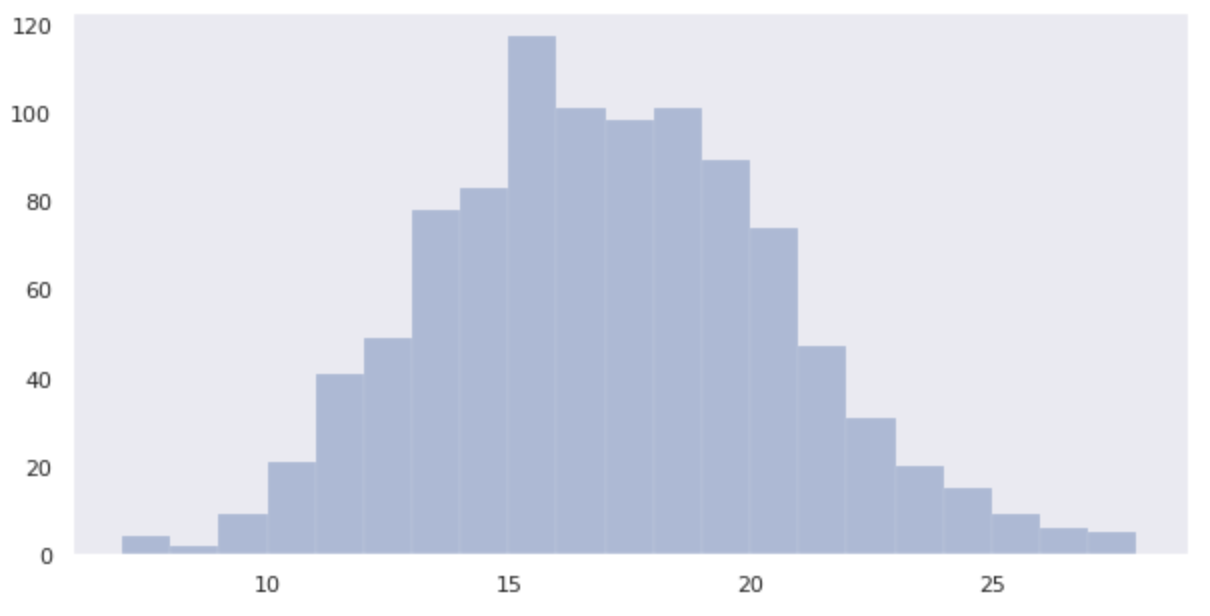
Anda bisa melihat bahwa distribusinya lebih dekat ke distribusi normal daripada ketika dadu dilempar tiga kali.