Apa itu distribusi Poisson

Distribusi Poisson adalah distribusi probabilitas yang diikuti oleh probabilitas suatu peristiwa yang terjadi sebanyak k kali, dengan rata-rata \lambda kali per satuan waktu (periode). Distribusi Poisson sering diterapkan pada masalah dunia nyata. Sebagai contoh

• Probabilitas 10 orang per jam mengunjungi restoran yang melayani 1 orang per jam
• Probabilitas bahwa persimpangan dengan rata-rata 3 kecelakaan lalu lintas per hari tidak akan mengalami kecelakaan lalu lintas hari ini

Ketika variabel acak X mengikuti distribusi Poisson, probabilitas bahwa suatu peristiwa yang terjadi rata-rata \lambda kali dalam periode tertentu terjadi k kali dapat ditemukan dengan persamaan berikut.

Dari persamaan di atas, kita melihat bahwa distribusi Poisson hanya bergantung pada \lambda. Untuk \lambda dari 1, 10, 20, dan 50, distribusinya adalah sebagai berikut.

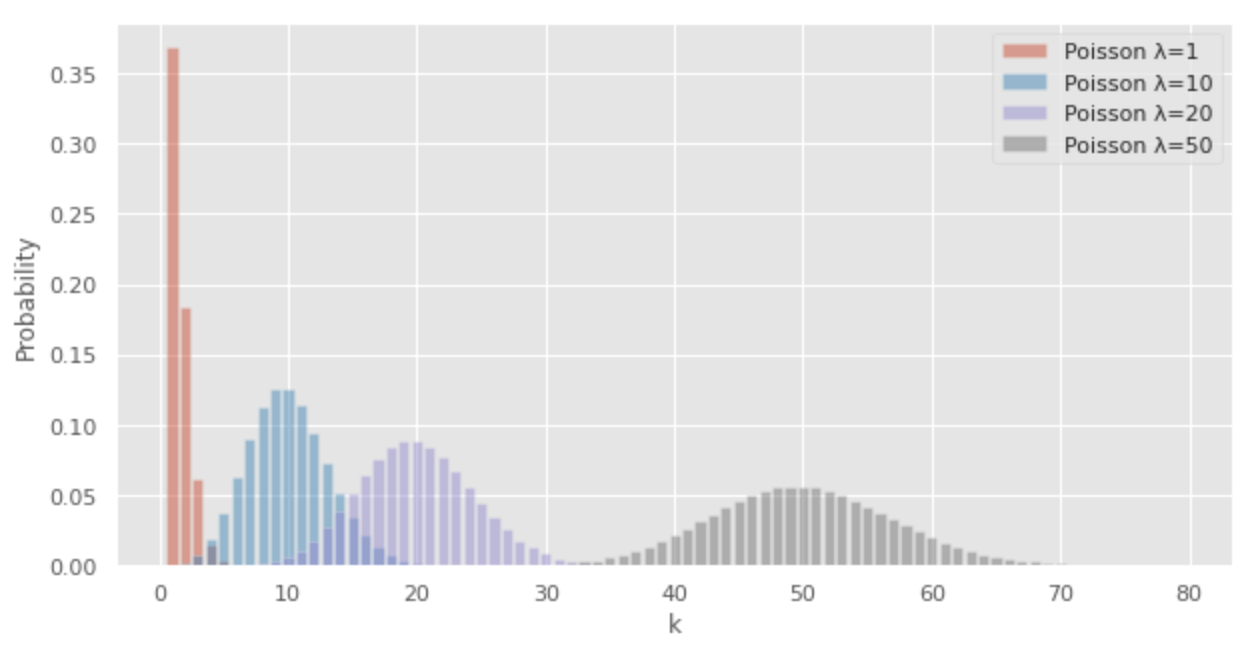
Semakin besar \lambda, semakin dekat distribusi mendekati distribusi normal.

Sebagai contoh perhitungan probabilitas untuk distribusi Poisson, mari kita cari probabilitas 10 pelanggan per jam di sebuah restoran yang melayani rata-rata 5 pelanggan per jam. Dalam kasus ini, \lambda=5 dan k=10. Hitung probabilitasnya sebagai berikut.

Probabilitas 10 pengunjung per jam adalah 1,8%.

Hubungan dengan distribusi binomial

Distribusi binomial adalah distribusi probabilitas bahwa berapa kali X suatu peristiwa benar-benar terjadi untuk sejumlah percobaan dengan probabilitas n sebagai p. Distribusi Poisson dapat diekspresikan dalam batas n \to \infty dan p \to 0, dengan distribusi binomial np konstan sebagai konstanta \lambda.

Dari persamaan di atas, untuk mengasumsikan bahwa suatu peristiwa mengikuti distribusi Poisson, kita perlu berurusan dengan nilai probabilitas p yang kecil, yaitu peristiwa yang jarang terjadi. Untuk alasan ini, distribusi Poisson sering menggunakan satuan waktu yang dapat dibatasi secara tak terhingga.

Probabilitas kecelakaan lalu lintas yang terjadi dalam satu detik sangat kecil. Dengan cara ini, waktu bisa sangat kecil dan probabilitas p bisa sedekat mungkin dengan 0, itulah sebabnya distribusi Poisson sering diterapkan.

Nilai yang diharapkan dan varians dari distribusi Poisson

Ekspektasi dan varians dari distribusi Poisson keduanya adalah \lambda.

Sifat reproduksi dari distribusi Poisson

Misalkan variabel acak X dan Y saling independen satu sama lain sesuai dengan distribusi Poisson, masing-masing, sebagai berikut.

Dalam hal ini, dari reprodusibilitas distribusi Poisson, X + Y mengikuti distribusi Poisson di bawah ini.

Kode Python

Kode Python berikut dapat digunakan untuk menggambar distribusi Poisson.

import numpy as np
from scipy.stats import poisson
import matplotlib.pyplot as plt

x =  np.arange(1, 80, 1)

# probability of the poisson distribution
y1= [poisson.pmf(i, 1) for i in x]
y10= [poisson.pmf(i, 10) for i in x]
y20= [poisson.pmf(i, 20) for i in x]
y50= [poisson.pmf(i, 50) for i in x]

# draw graph
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))
# plt.grid()

ax.bar(x,y1,alpha=0.5, label="Poisson λ=1")
ax.bar(x,y10,alpha=0.5, label="Poisson λ=10")
ax.bar(x,y20,alpha=0.5, label="Poisson λ=20")
ax.bar(x,y50,alpha=0.5, label="Poisson λ=50")

ax.legend()
ax.set_xlabel("k")
ax.set_ylabel("Probability")
plt.show()