Apa itu distribusi eksponensial

Distribusi eksponensial adalah distribusi probabilitas yang diikuti oleh waktu berikutnya x yang terjadi rata-rata \lambda kali per satuan waktu. Distribusi eksponensial digunakan dalam contoh berikut.

• Sebuah pusat panggilan di mana telepon berdering rata-rata 20 kali per jam, dan waktu sampai panggilan berikutnya berdering
• Waktu sampai terjadinya bencana berikutnya yang terjadi sekali setiap dua tahun

Fungsi densitas probabilitas dari distribusi eksponensial dapat dinyatakan sebagai berikut:

Di mana \lambda adalah rata-rata berapa kali peristiwa terjadi dalam satuan waktu dan x adalah periode waktu sampai peristiwa itu terjadi.

Distribusi eksponensial dari \lambda untuk \frac{1}{6}, \frac{1}{2}, 1, dan 2 adalah sebagai berikut.

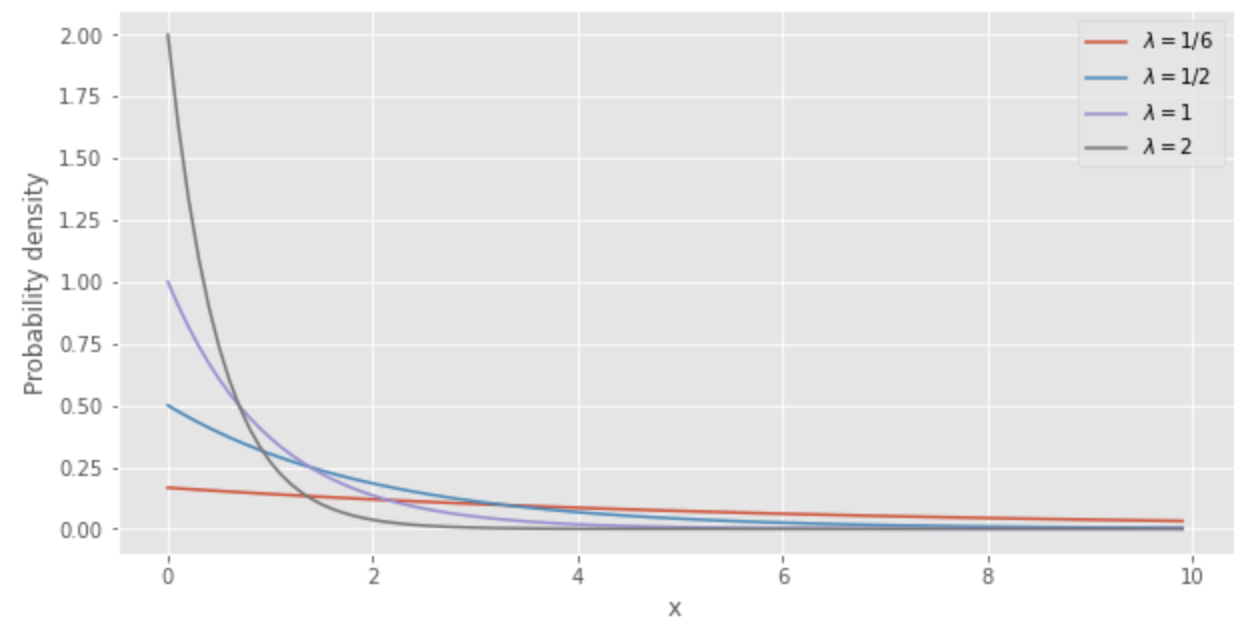
Semakin kecil nilai \lambda, semakin lambat penurunannya, dan semakin monotonik penurunannya, tidak tergantung pada nilai \lambda.

Nilai yang diharapkan dan varians dari distribusi eksponensial

Nilai yang diharapkan dan varians dari distribusi eksponensial masing-masing adalah:

Memoryless dari distribusi eksponensial

Jika variabel acak X mengikuti distribusi eksponensial dan m, n > 0, persamaan berikut berlaku

Persamaan di atas mengimplikasikan bahwa waktu sampai terjadinya suatu kejadian di masa depan tidak tergantung pada keberadaan kejadian di masa lalu. Sifat ini disebut memoryless. Distribusi eksponensial adalah satu-satunya distribusi kontinu dengan memoryless.

Hubungan dengan distribusi Poisson

Distribusi eksponensial adalah distribusi probabilitas yang mengikuti waktu yang dibutuhkan untuk terjadinya suatu peristiwa, sedangkan distribusi Poisson adalah distribusi probabilitas yang mengikuti jumlah berapa kali suatu peristiwa terjadi dalam satuan waktu. Dengan kata lain, distribusi eksponensial mempertimbangkan peristiwa yang sama dalam hal waktu, sedangkan distribusi Poisson mempertimbangkannya dalam hal berapa kali.

Kode Python

Kode Python berikut dapat digunakan untuk memplot distribusi eksponensial.

from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

x = np.arange(0, 10, 0.1)
y_1_6 = expon.pdf(x=x, scale=6)
y_1_2 = expon.pdf(x=x, scale=2)
y_1 = expon.pdf(x=x, scale=1)
y_2 = expon.pdf(x=x, scale=1/2)
plt.plot(x, y_1_6, label='$\lambda=1/6$')
plt.plot(x, y_1_2, label='$\lambda=1/2$')
plt.plot(x, y_1, label='$\lambda=1$')
plt.plot(x, y_2, label='$\lambda=2$')
plt.legend()
plt.xlabel("x")
plt.ylabel("Probability density")