Apa itu distribusi gamma
Distribusi gamma adalah distribusi probabilitas yang diikuti oleh
- Berat badan seseorang
- Masa inkubasi virus
- Latensi terhadap waktu henti sistem
- Masa hidup komponen elektronik
Fungsi densitas probabilitas dari distribusi gamma dinyatakan oleh persamaan berikut ini:
Distribusi gamma memiliki
Hubungan dengan distribusi eksponensial
Distribusi eksponensial bertepatan dengan distribusi gamma ketika
Dengan mensubstitusikan
Persamaan di atas konsisten dengan fungsi kepadatan probabilitas dari distribusi eksponensial yang nilai harapannya adalah
Nilai yang diharapkan dan varians dari distribusi gamma
Nilai yang diharapkan dan varians dari distribusi gamma masing-masing adalah:
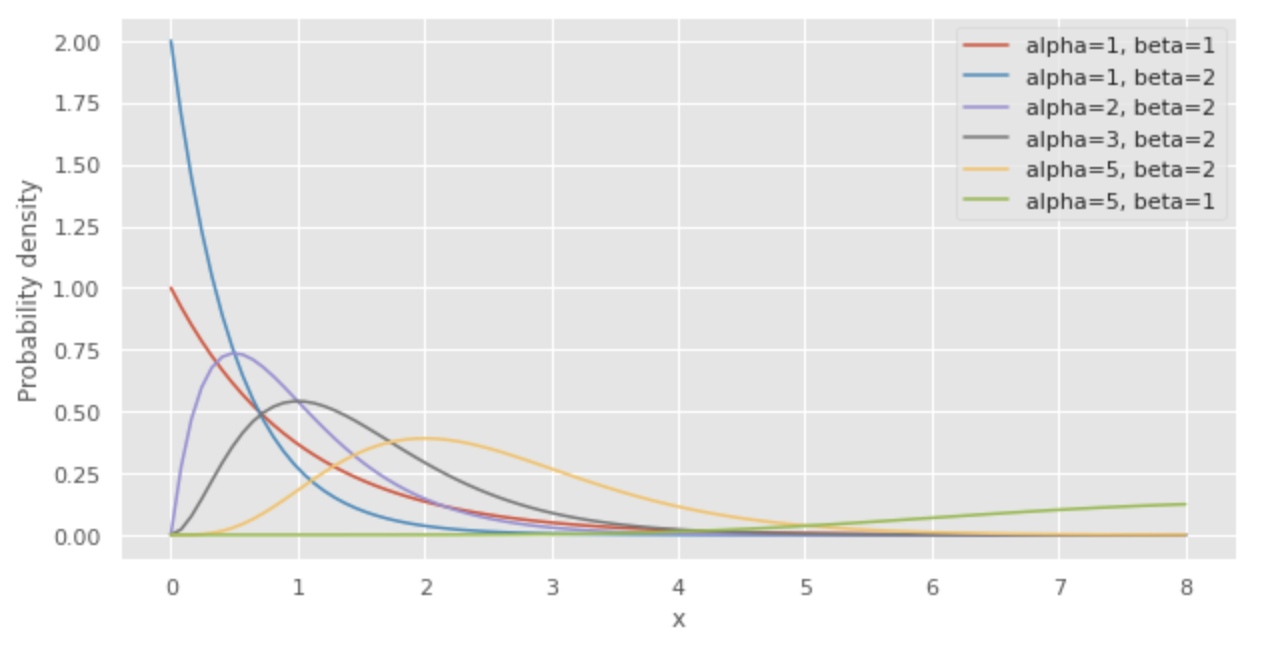
Pengaruh parameter pada distribusi gamma
Visualisasikan efek dari parameter
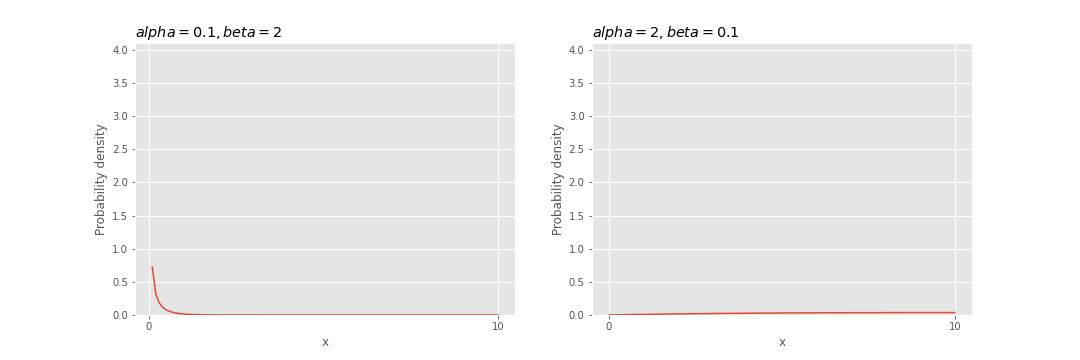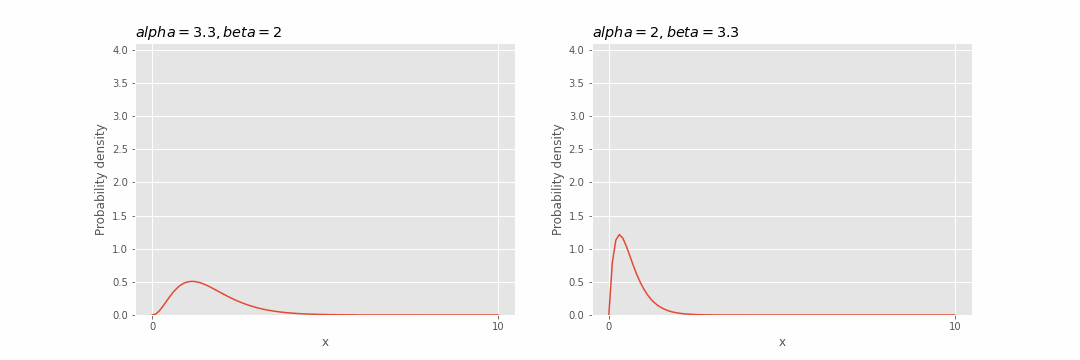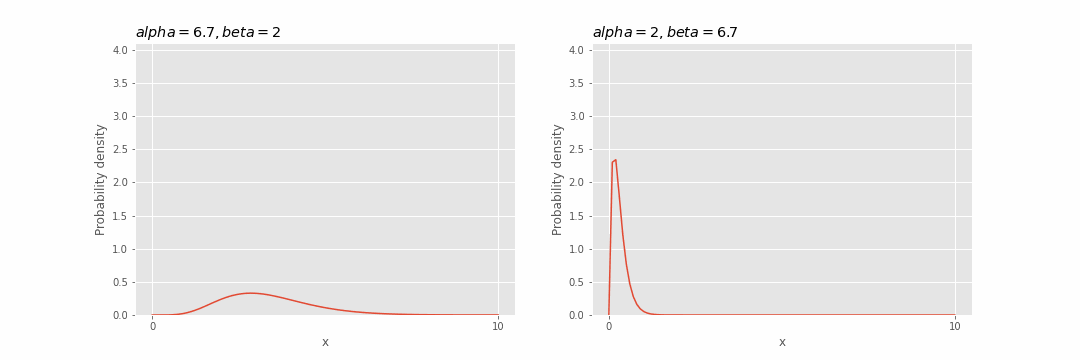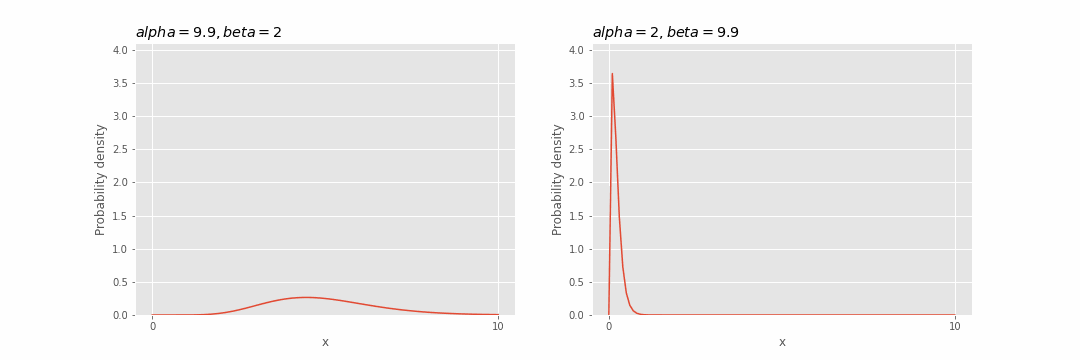
Kita dapat melihat bahwa semakin besar
Sifat reproduksi dari distribusi gamma
Misalkan variabel acak
Kemudian, dari properti reproduksi distribusi gamma,
Kode Python
Kode Python yang digunakan dalam proyek ini adalah sebagai berikut.
Menggambar distribusi gamma
import numpy as np
from scipy.stats import gamma
import matplotlib.pyplot as plt
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(10, 5))
# x axis
x = np.linspace(0, 8, 100)
# draw graph
plt.plot(x, gamma.pdf(x, 1, 0, scale=1/1), label='alpha=1, beta=1')
plt.plot(x, gamma.pdf(x, 1, 0, scale=1/2), label='alpha=1, beta=2')
plt.plot(x, gamma.pdf(x, 2, 0, scale=1/2), label='alpha=2, beta=2')
plt.plot(x, gamma.pdf(x, 3, 0, scale=1/2), label='alpha=3, beta=2')
plt.plot(x, gamma.pdf(x, 5, 0, scale=1/2), label='alpha=5, beta=2')
plt.plot(x, gamma.pdf(x, 10, 0, scale=1/1), label='alpha=5, beta=1')
plt.legend()
plt.xlabel("x")
plt.ylabel("Probability density")
plt.show()
Mengambar efek parameter pada distribusi gamma
import numpy as np
from scipy.stats import gamma
import matplotlib
import matplotlib.pyplot as plt
from matplotlib import animation, rc
from matplotlib.animation import FuncAnimation
rc('animation', html='html5')
np.random.seed(5)
# Set up formatting for the movie files
Writer = animation.writers['ffmpeg']
writer = Writer(fps=15, metadata=dict(artist='Me'), bitrate=1800)
prob_vals = np.arange(start=0.1, stop=10.01, step=0.2)
plt.style.use('ggplot')
fig, ax = plt.subplots(facecolor="w", figsize=(15, 5))
# x axis
x = np.linspace(0, 10, 100)
def update(i):
p = prob_vals[i]
# alpha graph
plt.subplot(1, 2, 1)
plt.cla()
plt.plot(x, gamma.pdf(x, round(p, 1), 0, scale=1/2))
# plt.plot(x, gamma.pdf(x, 2, 0, scale=1/round(p, 1)))
plt.title(f'$alpha={str(round(p, 1))}, beta=2$', loc='left')
plt.xlabel("x")
plt.ylabel("Probability density")
plt.ylim(0, 4.1)
plt.xticks(ticks=[0, 10]) # x axis ticks
# beta graph
plt.subplot(1, 2, 2)
plt.cla()
plt.plot(x, gamma.pdf(x, 2, 0, scale=1/round(p, 1)))
plt.title(f'$alpha=2, beta={str(round(p, 1))}$', loc='left')
plt.xlabel("x")
plt.ylabel("Probability density")
plt.ylim(0, 4.1)
plt.xticks(ticks=[0, 10]) # x axis ticks
anime_prob = FuncAnimation(fig, update, frames=len(prob_vals), interval=1000)
anime_prob.save('gamma_dist.gif', writer='pillow', fps=10)
Ryusei Kakujo
Focusing on data science for mobility
Bench Press 100kg!