2022-12-23

統計モデル

Statistics

Statistical Model

Python

統計モデルとは

統計モデルとは、観測されたデータについてパターンであったり法則性を説明する数理モデルです。データの特徴に合わせて確率分布を選択し、観測データをうまく説明できるような確率分布のパラメータを推定します。

パラメータ推定

次のサンプルサイズが50の標本データについて、Pythonでパラメータ推定を行なっていきます。

data = [2,2,4,6,4,5,2,3,1,2,0,4,3,3,3,3,4,2,7,2,4,3,3,3,4,
        3,7,5,3,1,7,6,4,6,5,2,4,7,2,2,6,2,4,5,4,5,1,3,2,3]

データの調査

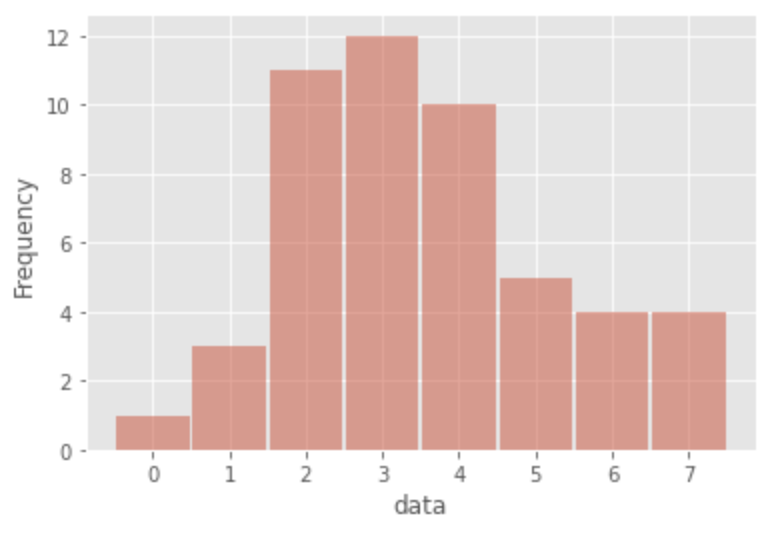
まずはデータのヒストグラムを見ます。

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

data = [2,2,4,6,4,5,2,3,1,2,0,4,3,3,3,3,4,2,7,2,4,3,3,3,4,
        3,7,5,3,1,7,6,4,6,5,2,4,7,2,2,6,2,4,5,4,5,1,3,2,3]

plt.hist(data, bins = [-0.5 + v for v in range(max(data) + 2)], alpha=0.5, rwidth=0.95)
plt.xlabel('data')
plt.ylabel('Frequency')

Histogram

次にデータの概要を見ます。

import pandas as pd

df = pd.DataFrame(data, columns=['x'])
df.describe()

	x
count	50.00000
mean	3.56000
std	1.72804
min	0.00000
25%	2.00000
50%	3.00000
75%	4.75000
max	7.00000

標本分散を見ます。

# sample variabce
df.var()

2.986122

調査により、次のことが確認できます。

山のような分布
データはカウントデータ（非負の整数）
標本平均は3.56
標本分散は2.99

確率分布の仮定

標本データから、母集団が従う確率分布を仮定します。標本データについて次のことが分かっています。

データがカウントデータ
下限は0であるが上限は不明
標本平均が3.56、標本分散が2.99であり比較的近い値

上記の特徴より、 $\lambda=3.56$ のポアソン分布を仮定します。

ポアソン分布と標本分布の比較

$\lambda=3.56$ のポアソン分布と標本データの分布を重ねて可視化してみます。

fig, ax1 = plt.subplots()
plt.hist(data, bins = [-0.5 + v for v in range(max(data) + 2)], alpha=0.5, rwidth=0.95)
poisson_values = poisson.rvs(3.56, size=10000)
prod = (pd.value_counts(poisson_values) / 10000).sort_index()
ax2 = ax1.twinx()
ax2.plot(prod)
plt.show()

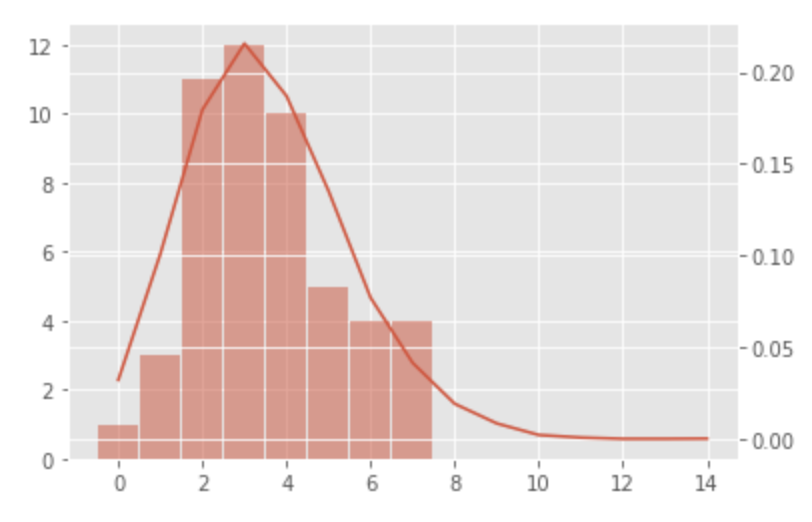
Poisson distribution with histogram

標本データの分布が $\lambda=3.56$ のポアソン分布で表現できているように見えます。

仮定した確率分布のパラメータ推定

確率分布のパラメータを標本データをもとに推定します。ここでは最尤推定法というパラメータ推定の方法を用います。

最尤推定法とは、尤度という観測データへの当てはまりの良さを表す統計量を最大にするパラメータを探索するパラメータ推定法です。今回ではパラメータは $\lambda$ になります。つまり、データへの当てはまりを最大化する $\lambda$ の値を推定することになります。

尤度は全ての標本データについての確率の積になります。尤度はパラメータの関数あり、 $L$ で表されます。今回のパラメータは $\lambda$ なので尤度を表す式は次のようになります。

L(\lambda) = \prod_i p(y_i | \lambda) = \prod_i \frac{e^{-\lambda} \lambda^y_i}{y_i!}

ここで、 $y_i$ は観測値です。今回の例でいうと $y_1=2, y_2=2, y_3=4, \cdots, y_{50}=3$ になります。

尤度 $L(\lambda)$ を最大化する $\lambda$ を調べます。ただ、尤度はそのままだと掛け算になっており扱いにくいため、対数変換した対数尤度を使ってパラメータの最尤推定を行います。

\log L(\lambda) = \sum_i (y_i \log \lambda - \lambda - \sum^{y_i}_k \log k)

次の図にパラメータ $\lambda$ を3.2から4.4まで変化させた場合の、分布の形状と $log L(\lambda)$ の値を示します。

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import sympy
from scipy.stats import poisson
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

lams = np.arange(3.2,4.5,0.4)

for i, lam in enumerate(lams):
    log_l = 0
    for y in data:
        f = (lam**y)*sympy.exp(-lam)/sympy.factorial(y)
        logf=sympy.log(f)
        log_l = log_l + logf

    fig, ax = plt.subplots()
    ax.hist(data, bins = [-0.5 + v for v in range(max(data) + 2)], alpha=0.5, rwidth=0.95)
    poisson_values = poisson.rvs(lam, size=10000)
    prod = (pd.value_counts(poisson_values) / 10000).sort_index()
    ax2 = ax.twinx()
    ax2.plot(prod, label=f'lambda={round(lam, 1)}, log L={round(log_l, 1)}')
    plt.legend()
    plt.show()

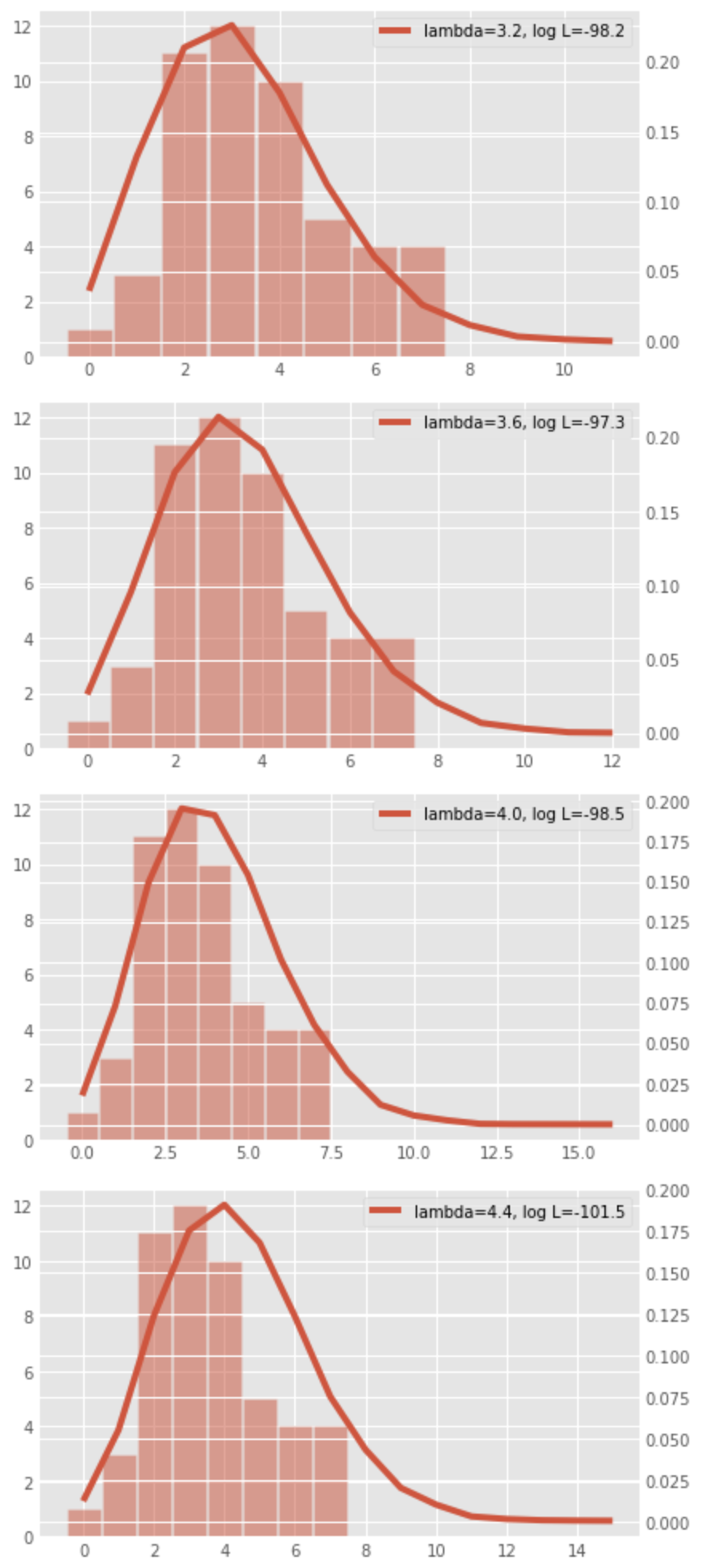
lambda and log maximum likelihood

$\lambda=3.6$ あたりで対数尤度が最大になりそうなことが分かります。対数尤度は $log L$ は尤度 $L$ の単調増加関数なので対数尤度が最大となる $\lambda$ において尤度も最大になります。

対数尤度の最大値を導出するには対数尤度をパラメータ $\lambda$ で偏微分したものが0となる $\lambda$ を探し出せば良いということになります。

\frac{\partial \log L(\lambda)}{\partial \lambda} = \sum_i (\frac{y_i}{\lambda} -1) = 0

上式を計算すると、 $\lambda=3.56$ のときに尤度が最大化されることが分かります。

統計モデルにどの確率分布を使えば良いか

観測データを説明する統計モデルの確率分布を選ぶ際には次の点に着目します。

データの種類（離散であるか連続であるか）
データの範囲
標本分散と標本平均の関係

いくつかの確率分布について、統計モデルの確率分布として使用できそうな必要条件は次のようになります。

データの種類	データの範囲	標本分散 $V(X)$ と標本平均 $E(X)$ の関係	確率分布
離散	$\{0, 1, 2, \cdots ,\infty \}$	$E(X) \approx V(X)$	ポアソン分布
離散	$\{0, 1, 2, \cdots ,\infty \}$	$E(X) < V(X)$	負の二項分布
離散	$\{0, 1, 2, \cdots ,N \}$		二項分布
連続	$[−\infty, \infty]$		正規分布
連続	$[0, \infty]$		対数正規分布
連続	$[0, \infty]$		ガンマ分布
連続	$[0, 1]$		ベータ分布