一般化線形モデル(GLM)とは
一般化線形モデル (Generalized Linear Model; GLM)とは、目的変数が正規分布以外の確率分布に従う場合であっても適用できる統計モデルです。
単回帰分析や重回帰分析は線形モデルと呼ばれるもので、目的変数が正規分布に従うと仮定した統計モデルです。目的変数が正規分布に従うと仮定できない場合、例えば目的変数がカテゴリカル、カウントデータのような離散変数の場合は線形モデルは適用できません。GLMでは正規分布だけでなく、二項分布、 ガンマ分布、 ポアソン分布といった指数型分布族と呼ばれる分布も扱うことができます。
GLMでは、目的変数と説明変数との関係式は簡単な線形式である必要はなく、次のように表すことができます。
確率分布とリンク関数の組み合わせ
よく使われる確率分布とリンク関数の組み合わせは以下になります。
| 確率分布 | リンク関数 | |
|---|---|---|
| 離散 | 二項分布 | logit |
| 離散 | ポアソン分布 | log |
| 離散 | 負の二項分布 | log |
| 連続 | ガンマ分布 | log |
| 連続 | 正規分布 | identity |
GLM の構築
実際にGLMを構築してみます。ここでは、ある架空の植物100個体の種子数データについて考えます。データは次のカラムで構成されています。
- y: 個体の種子数
- x: 個体のサイズ
- f: 個体に施肥処理をしたかどうか(C: 施肥処理をしていない、T: 施肥処理をしている)
import pandas as pd
# number of seeds
y = [6,6,6,12,10,4,9,9,9,11,6,10,6,10,11,8,3,8,5,5,4,11,5,10,6,6,7,9,3,10,2,9,10,
5,11,10,4,8,9,12,8,9,8,6,6,10,10,9,12,6,14,6,7,9,6,7,9,13,9,13,7,8,10,7,12,
6,15,3,4,6,10,8,8,7,5,6,8,9,9,6,7,10,6,11,11,11,5,6,4,5,6,5,8,5,9,8,6,8,7,9]
# body size
x = [8.31,9.44,9.5,9.07,10.16,8.32,10.61,10.06,9.93,10.43,10.36,10.15,10.92,8.85,
9.42,11.11,8.02,11.93,8.55,7.19,9.83,10.79,8.89,10.09,11.63,10.21,9.45,10.44,
9.44,10.48,9.43,10.32,10.33,8.5,9.41,8.96,9.67,10.26,10.36,11.8,10.94,10.25,
8.74,10.46,9.37,9.74,8.95,8.74,11.32,9.25,10.14,9.05,9.89,8.76,12.04,9.91,
9.84,11.87,10.16,9.34,10.17,10.99,9.19,10.67,10.96,10.55,9.69,10.91,9.6,
12.37,10.54,11.3,12.4,10.18,9.53,10.24,11.76,9.52,10.4,9.96,10.3,11.54,9.42,
11.28,9.73,10.78,10.21,10.51,10.73,8.85,11.2,9.86,11.54,10.03,11.88,9.15,8.52,
10.24,10.86,9.97]
# feed (C: control, T: treatment)
f = ['C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
'C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
'C','C','C','C','C','C','C','C','C','C','C','C','T','T','T','T','T','T','T',
'T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
'T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
'T','T','T','T','T']
df = pd.DataFrame(list(zip(y, x, f)), columns =['y', 'x', 'f'])
display(df.head())
| y | x | f | |
|---|---|---|---|
| 0 | 6 | 8.31 | C |
| 1 | 6 | 9.44 | C |
| 2 | 6 | 9.50 | C |
| 3 | 12 | 9.07 | C |
| 4 | 10 | 10.16 | C |
データの確認
記述統計量を確認します。
df.describe()
| y | x | |
|---|---|---|
| count | 100.000000 | 100.000000 |
| mean | 7.830000 | 10.089100 |
| std | 2.624881 | 1.008049 |
| min | 2.000000 | 7.190000 |
| 25% | 6.000000 | 9.427500 |
| 50% | 8.000000 | 10.155000 |
| 75% | 10.000000 | 10.685000 |
| max | 15.000000 | 12.400000 |
fについてC、Tの数をそれぞれ表示します。
print('num of C:', len(df[df['f'] == 'C']))
print('num of T:', len(df[df['f'] == 'T']))
num of C: 50
num of T: 50
データの記述統計量から次のことが確認できます。
- 種子数y:
- 非負の整数となっている(2から15)
- 平均と分散がまあまあ近い
- 個体サイズx:
- 正の実数(連続値)となっている
- 分散は小さい
- 施肥処理の有無f:
- カテゴリ変数となっている
- 各カテゴリの要素数は均等になっている
次にデータの可視化を行います。まずは散布図を表示します。
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use('ggplot')
plt.figure(figsize=(10,5))
sns.set(rc={'figure.figsize':(10,5)})
sns.scatterplot(x='x', y='y', hue='f', data=df)
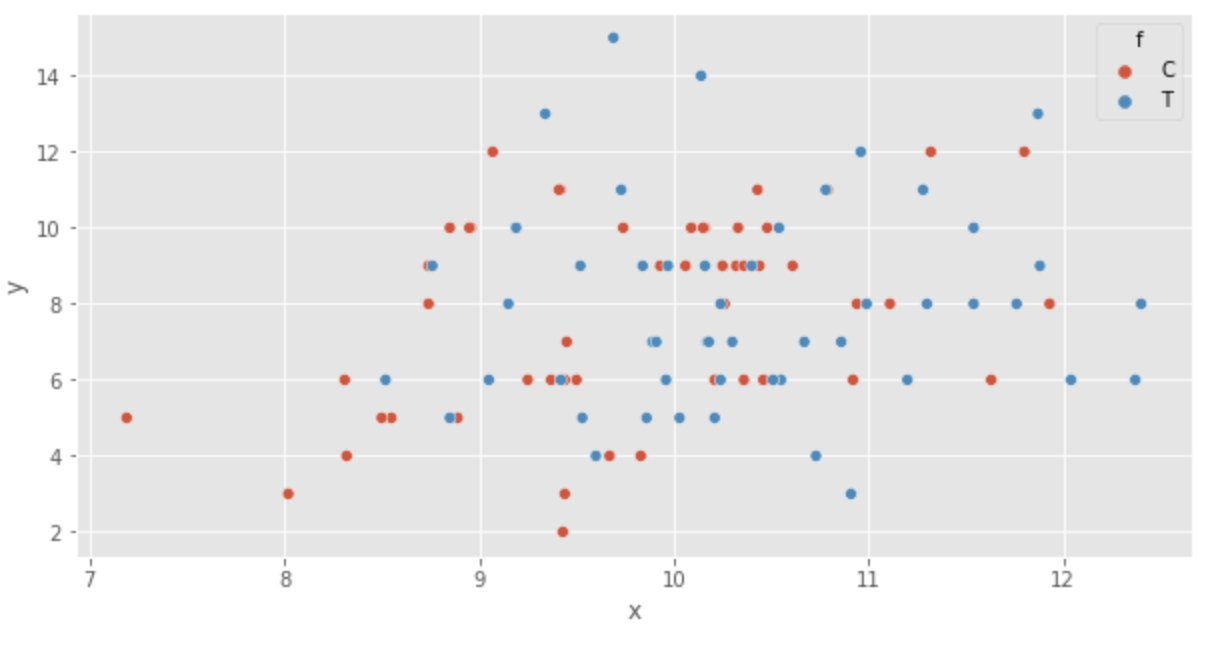
箱ヒゲ図を表示します。
sns.boxplot(x='f', y='y', data=df)
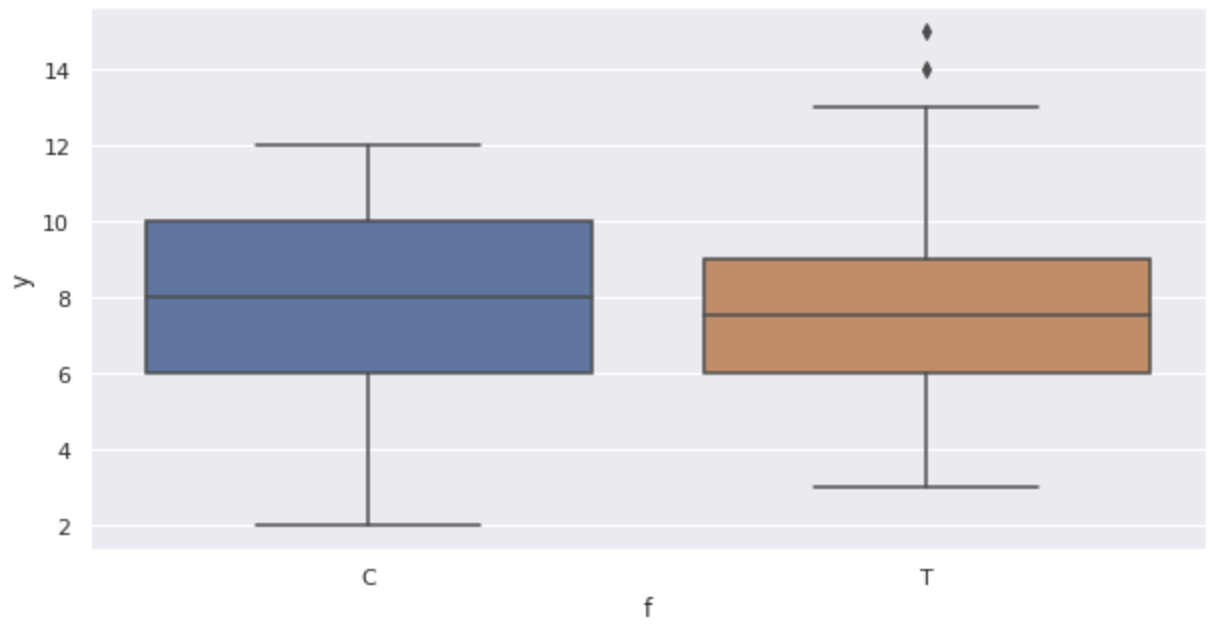
グラフから次のことが確認できます。
- サイズ
x - 肥料の効果は無いように見える(箱ヒゲ図)
ポアソン回帰で統計モデルの構築
ある架空の植物の個体
ポアソン分布には分布の形状を決めるパラメータ
- 種子数が個体のサイズに依存する統計モデル
- 種子数が施肥処理の有無に依存する統計モデル
- 種子数がサイズと施肥処理の有無に依存する統計モデル
種子数が個体のサイズに依存する統計モデル
個体ごとに異なる
ここで、
両辺対数を取ると次のようになります。
このとき、右辺
線形予測子に対する左辺の関数はリンク関数 link functionと呼ばれます。今回のリンク関数は
ポアソン回帰のGLMではよく対数リンク関数が使われます。その理由としては、ポアソン分布の平均
これから次の対数尤度関数を最大化する
パラメータの推定は次のPythonコードで簡単に行うことができます。
import statsmodels.api as sm
import statsmodels.formula.api as smf
fit_x = smf.glm('y ~ x', data=df, family=sm.families.Poisson()).fit()
fit_x.summary()
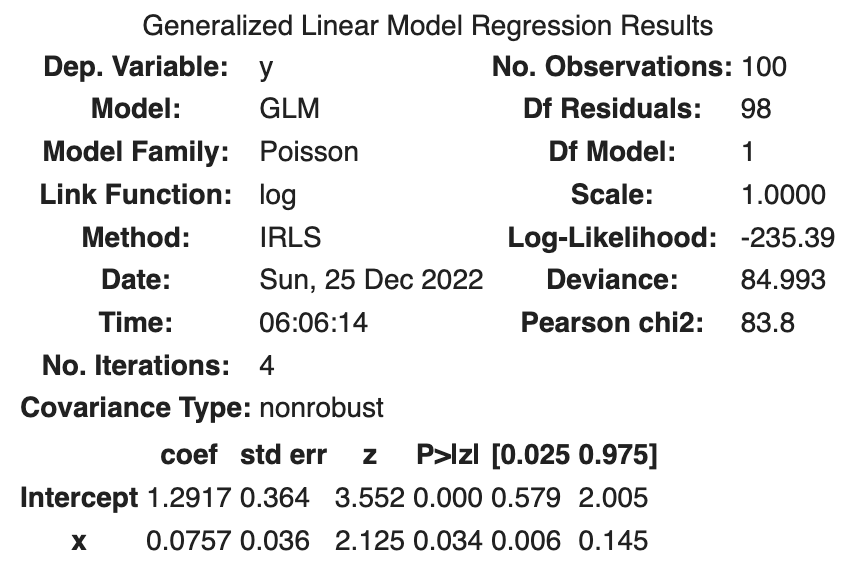
次の結果が得られました。
| coef | std err | z | Log-likelihood | |
|---|---|---|---|---|
| Intercept | 1.2917 | 0.364 | 3.552 | |
| x | 0.0757 | 0.036 | 2.125 | |
| -235.39 |
ここで、std errは標準誤差のことで、つまりは推定したパラメータの標準偏差になります。標準偏差の導出には正規分布を仮定しています。また、zは z 値のことです。
上記の関数をプロットしてみます。
import numpy as np
import math
sns.scatterplot(x='x', y='y', hue='f', data=df)
x = np.arange(df.x.min(), df.x.max() + 0.01, 0.01)
y = [math.exp(fit_x.params['Intercept'] + fit_x.params['x'] * x_i) for x_i in x]
plt.plot(x, y)
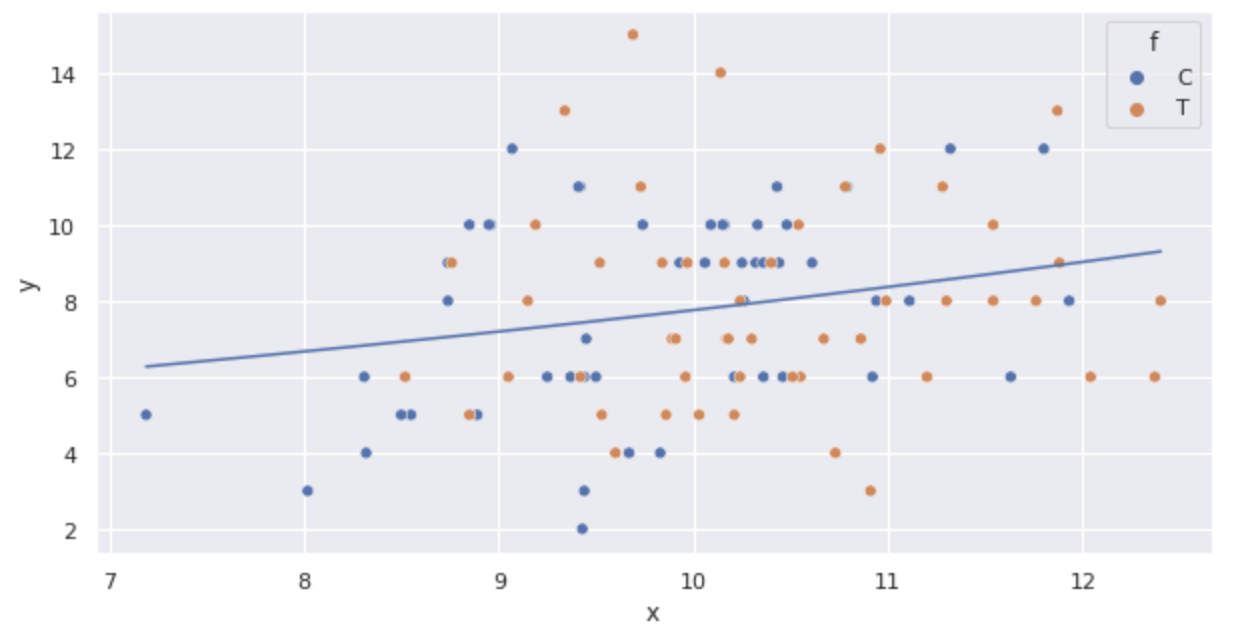
サイズ
種子数が施肥処理の有無に依存する統計モデル
施肥の有無
施肥の有無
モデルは次のようになります。
つまり、個体
となり、個体
となります。
次の対数尤度関数を最大化する
import statsmodels.api as sm
import statsmodels.formula.api as smf
fit_f = smf.glm('y ~ f', data=df, family=sm.families.Poisson()).fit()
fit_f.summary()

次の結果が得られました。
| coef | std err | z | Log-likelihood | |
|---|---|---|---|---|
| Intercept | 2.0516 | 0.051 | 40.463 | |
| f[T.T] | 0.0128 | 0.071 | 0.179 | |
| -237.63 |
つまり、
施肥処理を加えると平均種子数が少しだけ増えるという結果となりました。
log-likelihoodは-237.63となっており、
種子数がサイズと施肥処理の有無に依存する統計モデル
最後に、サイズ
モデルは次のようになります。
次の対数尤度関数を最大化する
import statsmodels.api as sm
import statsmodels.formula.api as smf
fit_full = smf.glm('y ~ x + f', data=df, family=sm.families.Poisson()).fit()
fit_full.summary()
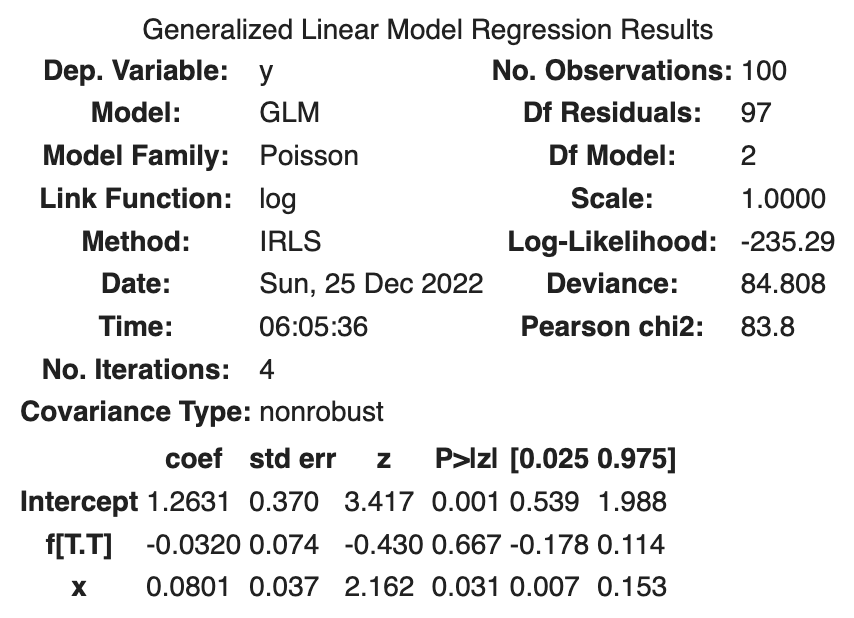
次の結果が得られました。
| coef | std err | z | Log-likelihood | |
|---|---|---|---|---|
| Intercept | 1.2631 | 0.370 | 3.417 | |
| f[T.T] | -0.0320 | 0.074 | -0.430 | |
| x | 0.0801 | 0.037 | 2.162 | |
| -235.29 |
つまり、
施肥処理を行うと平均種子数が少なくなると解釈されています。具体的には、
log-likelihoodは-235.29となっており、これまでの2つのモデルよりもデータに対する当てはまりが良くなっています。
参考