2022-04-01

回帰分析

回帰分析とは

回帰分析とは、変数間の関係を調べるための統計的手法です。1つまたは複数の独立変数の値に関連して、従属変数の値がどのように変化するかを理解することを可能にします。回帰分析は、特に従属変数の動向を予測し、変数間の因果関係を明らかにするために有用です。金融、経済、社会科学、工学など、様々な分野で広く用いられています。

回帰分析は、次のような理由で統計学において重要な役割を担っています。

予測モデリング
回帰分析により、独立変数の値に基づいて従属変数に関する予測を行うことができるモデルを作成することができます。これは、将来のトレンドの予測やデータに基づいた意思決定に特に有用です。
変数間の関係の評価
変数間の関係を数量化することで、回帰分析は関係の性質や強さに関する洞察を提供します。この情報は仮説検定や潜在的な因果関係を理解するために役立ちます。
影響を与える要因の特定
回帰分析により、独立変数が従属変数にもっとも大きな影響を与えるかどうかを特定することができます。この知識は、効果的な介入や戦略の開発に不可欠です。

条件付き平均

条件付き平均とは、独立変数の値に基づいて従属変数の期待値を指します。回帰分析では、フィットした回帰モデルによって条件付き平均が表されます。条件付き平均は、独立変数に基づいて従属変数の予測を行うために使用されます。

例えば、単回帰分析の場合、条件付き平均は次のように表されます。

E(Y|X) = \beta_0 + \beta_1X

ここで、 $E(Y|X)$ は、独立変数 $X$ の値に基づいて従属変数 $Y$ の期待値を示し、 $\beta_0$ と $\beta_1$ は回帰モデルのパラメータです。

条件付き分布

条件付き分布とは、独立変数の値に基づいて従属変数の分布を指します。条件付き分布は、従属変数のばらつきや形状を独立変数の各値について理解するのに役立ちます。

回帰分析では、条件付き分布はしばしばある種の確率分布の族に従うと仮定されます。例えば、線形回帰では、従属変数の条件付き分布が平均が条件付き平均であり、一定の分散（等分散性）を持つ正規分布に従うと仮定されます。

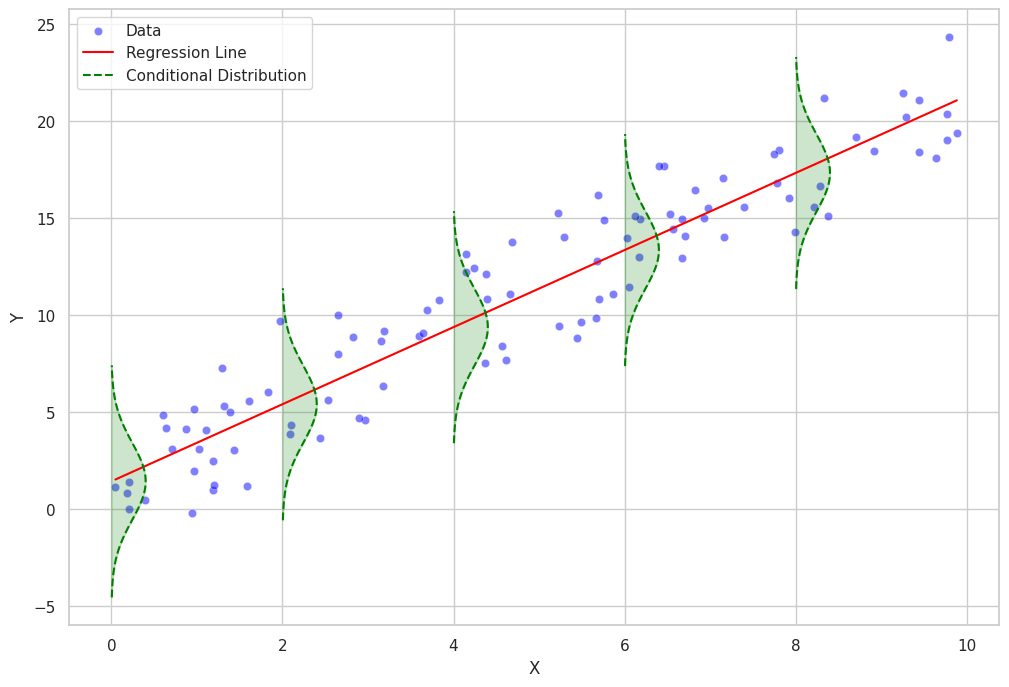
Conditional distribution

一方、一般化線形モデルや非パラメトリック回帰モデルなどのより複雑な回帰モデルでは、条件付き分布はポアソン分布、二項分布、ガンマ分布などの異なる確率分布族に従うことがあります。

最小二乗法

最小二乗法は、回帰モデルのパラメータを推定するための広く使われているアプローチです。観測された従属変数の値とモデルによって予測される値の差の二乗和を最小化することにより、最適な回帰線（線形回帰の場合）または曲線（非線形回帰の場合）を得ることができます。

最小二乗法の式

最小二乗法は、残差の二乗和を最小化することを目的としています。各観測値の残差とは、観測された従属変数の値と回帰モデルによって予測された値の差です。

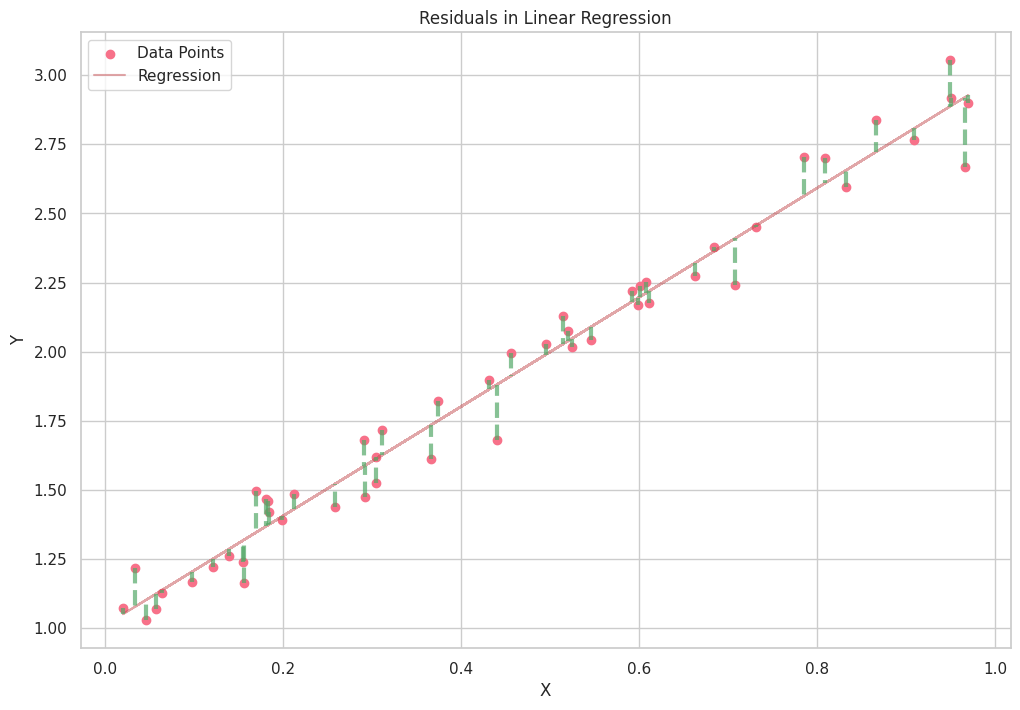
Residual

単回帰分析の場合、回帰モデルは次のように表されます。

Y_i = \beta_0 + \beta_1X_i + \epsilon_i

ここで、 $Y_i$ は $i$ 番目の観測値の従属変数の値、 $X_i$ は $i$ 番目の観測値の独立変数の値、 $\beta_0$ と $\beta_1$ は推定されるパラメータ（切片と傾き）、 $\epsilon_i$ は $i$ 番目の観測値の残差です。

最小二乗法の目的は、次の式で表される残差の二乗和を最小化する $\beta_0$ と $\beta_1$ の値を求めることです。

S(\beta_0, \beta_1) = \sum_{i=1}^{n} \epsilon_i^2 = \sum_{i=1}^{n} (Y_i - \beta_0 - \beta_1X_i)^2

$S(\beta_0, \beta_1)$ を最小化するために、 $\beta_0$ と $\beta_1$ に関する偏微分を0に設定します。

\frac{\partial S}{\partial \beta_0} = -2\sum_{i=1}^{n} (Y_i - \beta_0 - \beta_1X_i) = 0

\frac{\partial S}{\partial \beta_1} = -2\sum_{i=1}^{n} X_i(Y_i - \beta_0 - \beta_1X_i) = 0

これらの方程式を同時に解くことで、 $\beta_0$ と $\beta_1$ の推定値を求めることができます。

\hat{\beta}_1 = \frac{\sum_{i=1}^{n} (X_i - \bar{X})(Y_i - \bar{Y})}{\sum_{i=1}^{n} (X_i - \bar{X})^2}

\hat{\beta}_0 = \bar{Y} - \hat{\beta}_1\bar{X}

ここで、 $\bar{X}$ と $\bar{Y}$ は、独立変数と従属変数の平均値を表します。

回帰分析の実装

この章では、Pythonを使った回帰分析の実装方法を説明します。

まず、必要なライブラリをインポートします。

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression

次に、線形回帰分析用のサンプルデータを作成します。

python

# Set a random seed for reproducibility
np.random.seed(42)

# Create the sample data
x = np.random.rand(50)
y = 2 * x + 1 + np.random.normal(0, 0.1, size=50)

# Store the data in a pandas DataFrame
data = pd.DataFrame({'X': x, 'Y': y})

次に、データに線形回帰モデルを当てはめます。

python

# Fit a linear regression model
model = LinearRegression()
model.fit(data[['X']], data['Y'])

# Calculate the predicted values
data['Y_pred'] = model.predict(data[['X']])

データ点と回帰直線のプロットを作成します。

python

# Set the style and color palette for the plot
sns.set_style("whitegrid")
sns.set_palette("husl")

# Create a scatter plot of the data points
plt.scatter(data['X'], data['Y'], label='Data Points')

# Plot the regression line
plt.plot(data['X'], data['Y_pred'], color='r', label='Regression Line')

# Add labels and a legend
plt.xlabel("X")
plt.ylabel("Y")
plt.legend(loc='best')
plt.title("Data Points and Regression Line")

# Show the plot
plt.show()

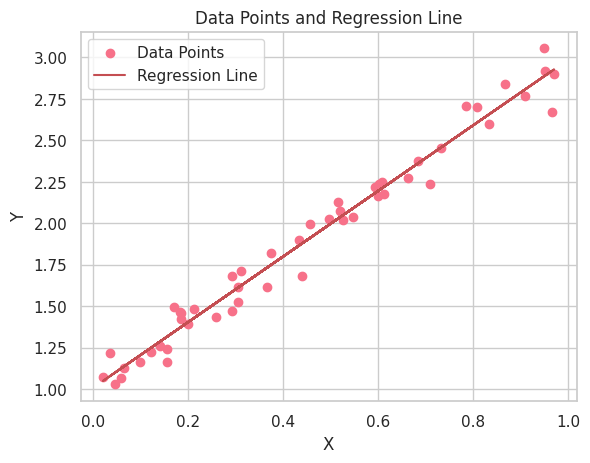
Regression

線形回帰分析の結果を解釈します。回帰直線が正の傾きを持つことから、XとYの変数間に正の関係があることが分かります。つまり、Xの値が増えるにつれて、Yの値も増加することを示しています。

データと回帰直線を視覚化するだけでなく、線形回帰モデルの推定パラメータ（係数）の解釈も重要です。線形回帰方程式は次のように書けます。

Y = \beta_0 + \beta_1X + \epsilon

ここで、 $Y$ は従属変数、 $X$ は独立変数、 $\beta_0$ と $\beta_1$ は推定された係数、 $\epsilon$ は残差（誤差項）を表します。

$\beta_0$ （切片）は、 $X$ が0の場合の $Y$ の推定値を表し、 $\beta_1$ （傾き）は、 $X$ が1単位増加した場合の $Y$ の推定値の変化を表します。

線形回帰モデルから推定されたパラメータを取得し、解釈します。

python

# Get the estimated parameters
intercept, slope = model.intercept_, model.coef_[0]

print(f"Intercept (β0): {intercept:.3f}")
print(f"Slope (β1): {slope:.3f}")

Intercept (β0): 1.010
Slope (β1): 1.978

この例では、推定された切片 $\beta_0$ は約1であり、推定された傾き $\beta_1$ は約2です。つまり、 $X$ が0の場合、 $Y$ の予測値は約1であり、 $X$ が1単位増加するごとに、 $Y$ の予測値が約2単位増加することを示しています。

このサンプルデータの $X$ と $Y$ の真の関係は、 $Y = 1 + 2X + noise$ です。推定されたパラメータが真の係数に近いことから、線形回帰モデルが変数間の真の関係を効果的に捉えていることが分かります。ただし、現実世界では、変数間の真の関係が不明な場合が多いです、回帰分析の目的は、推定されたパラメータに基づいて予測を行うことです。

条件付き分布と残差のプロットのためのPythonコード

以下は、条件付き分布と残差をプロットするためのPythonコードです。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from scipy.stats import norm

# Set seaborn style
sns.set(style="whitegrid")

# Generate a dataset
np.random.seed(0)
n = 100
x = np.random.uniform(0, 10, n)
y = 2 * x + 1 + np.random.normal(0, 2, n)
data = pd.DataFrame({"x": x, "y": y})

# Fit a linear regression model
model = LinearRegression()
model.fit(data[["x"]], data["y"])


# Add regression line to the dataset
data["y_pred"] = model.predict(data[["x"]])

rmse = np.sqrt(mean_squared_error(data["y"], data["y_pred"]))

def plot_conditional_distributions_filled(data, intervals, model):
    fig, ax = plt.subplots(figsize=(12, 8))

    # Scatter plot of the data points
    sns.scatterplot(data=data, x="x", y="y", color="blue", alpha=0.5, label="Data", ax=ax)

    # Regression line
    sns.lineplot(data=data, x="x", y="y_pred", color="red", label="Regression Line", ax=ax)


    for i in range(len(intervals) - 1):
        lower = intervals[i]
        upper = intervals[i + 1]
        mask = (data["x"] >= lower) & (data["x"] < upper)

        if mask.sum() > 0:
            subset = data[mask]
            mean = model.intercept_ + model.coef_[0] * lower
            std = rmse

            # Plot Gaussian curve
            x_vals = np.linspace(mean - 3 * std, mean + 3 * std, 100)
            y_vals = norm.pdf(x_vals, mean, std)
            y_vals = y_vals * (upper - lower) + lower

            ax.plot(y_vals, x_vals, color="green", linestyle="--", label="Conditional Distribution" if i == 0 else None)

            # Fill the Gaussian curve
            ax.fill_betweenx(x_vals, lower, y_vals, color="green", alpha=0.2)

    ax.set_xlabel("X")
    ax.set_ylabel("Y")
    ax.legend()
    plt.show()

# Define intervals for Gaussian curves
intervals = np.arange(0, 12, 2)

# Plot the conditional distributions with filled Gaussian curves
plot_conditional_distributions_filled(data, intervals, model)

Conditional distribution

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression

# Set a random seed for reproducibility
np.random.seed(42)

# Create the sample data
x = np.random.rand(50)
y = 2 * x + 1 + np.random.normal(0, 0.1, size=50)

# Store the data in a pandas DataFrame
data = pd.DataFrame({'X': x, 'Y': y})

# Fit a linear regression model
model = LinearRegression()
model.fit(data[['X']], data['Y'])

# Calculate the predicted values
data['Y_pred'] = model.predict(data[['X']])

# Set the style and color palette for the plot
sns.set_style("whitegrid")
sns.set_palette("husl")

plt.subplots(figsize=(12, 8))

# Create a scatter plot of the data points
plt.scatter(data['X'], data['Y'], label='Data Points')

# Plot the regression line
plt.plot(data['X'], data['Y_pred'], color='r', label='Regression', alpha=0.5)

# Calculate and plot the residuals
for _, row in data.iterrows():
    plt.plot([row['X'], row['X']], [row['Y'], row['Y_pred']], color='g', linewidth=3, linestyle='--', alpha=0.7)

# Add labels and a legend
plt.xlabel("X")
plt.ylabel("Y")
plt.legend(loc='best')
plt.title("Residuals in Linear Regression")

# Show the plot
plt.show()