2022-11-20

線形回帰

Machine Learning

Regression

Python

sklearn

線形回帰とは

線形回帰とは、1つまたは複数の独立変数（説明変数、特徴量、入力変数とも呼ばれます）と従属変数（応答変数、結果変数、目的変数とも呼ばれます）の関係をモデル化するために使用される機械学習アルゴリズムです。線形回帰の主要な目的は、従属変数の値を独立変数の値に基づいて予測することです。これは、観測されたデータ点に線形方程式を当てはめることで実現されます。簡単な線形回帰の場合、これは直線として表現され、複数の線形回帰の場合はハイパープレーンとして表現されます。

線形回帰の基礎原理は、予測値と実測値の差を最小化することにあります。この差は残差と呼ばれ、データ点と当てはめられた直線またはハイパープレーンの垂直距離です。残差の二乗和を最小化することにより、従属変数に関する予測モデルに最適な当てはめ直線またはハイパープレーンを得ることができます。

線形回帰の前提条件

線形回帰モデルが正確で信頼性の高い予測を提供するためには、いくつかの前提条件を満たす必要があります。

直線性
従属変数と独立変数の間に直線的な関係がある必要があります。散布図または相関係数を使用して確認できます。
独立性
独立変数は互いに高度に相関していてはなりません。多重共線性は、不安定な推定値を導き、冗長な変数を削除するか、正則化技術を使用することで対処できます。
等分散性
残差の分散は、独立変数の全てのレベルで一定である必要があります。散布図や診断テストを使用して異分散性を検出し、重み最小二乗法または従属変数の変換を使用して対処することができます。
正規性
残差は、正規分布に従う必要があります。ヒストグラム、Q-Qプロット、またはShapiro-Wilkテストなどの統計テストを使用して確認できます。非正規性は、従属変数の変換またはロバスト回帰技術を使用することで対処できます。
誤差の独立性
残差は互いに独立している必要があります。Durbin-Watsonテストを使用するか、残差を時間または予測値に対してプロットすることで確認できます。自己相関は時系列モデルを使用するか、遅延変数を組み込むことによって対処できます。

単回帰分析

単回帰分析では、単一の独立変数（ $X$ ）と従属変数（ $Y$ ）の間に直線的な関係を確立することを目的としています。この関係の方程式は次のように書くことができます。

$Y = \beta_0 + \beta_1X + \epsilon$

$Y$ は従属変数
$X$ は独立変数
$\beta_0$ は直線のy切片（ $X$ が0のときの $Y$ の値）
$\beta_1$ は直線の傾き（ $X$ が1単位変化したときの $Y$ の変化）
$\epsilon$ は誤差項（ $Y$ の実測値と予測値の差）

最適な当てはめ直線は、残差の二乗和を最小化することで得られます。

最小二乗法

最小二乗法は、残差の二乗和を最小化することによって最適な当てはめ直線を見つけるための数学的手法です。最適な当てはめ直線のy切片と傾きの推定値は、次の式を使用して計算できます。

$\beta_1 = \frac{\sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})}{\sum_{i=1}^n (X_i - \bar{X})^2}$

$\beta_0 = \bar{Y} - \beta_1\bar{X}$

$n$ はデータ点の数
$X_iと$ Y_i$は個々のデータ点
$\bar{X}$ と $\bar{Y}$ は独立変数と従属変数の平均値

モデルのパフォーマンスの評価

最適な当てはめ直線を得たら、データに対して良好なフィットを示すかどうかを評価する必要があります。単回帰分析モデルの性能を評価するために使用される一般的なメトリックには、次のものがあります。

決定係数(R^2)

このメトリックは、従属変数の分散のうち独立変数で説明できる割合を測定します。 $R^2$ 値が1に近い場合、強い関係があります。 $R^2$ 値が0に近い場合、弱い関係があります。

$R^2 = 1 - \frac{\sum_{i=1}^n (Y_i - \hat{Y}i)^2}{\sum{i=1}^n (Y_i - \bar{Y})^2}$

ここで、 $\hat{Y}_i$ は $i$ 番目のデータ点に対する予測値です。

平均二乗誤差(MSE)

このメトリックは、従属変数の実測値と予測値の差の平均二乗値を計算します。

$MSE = \frac{1}{n}\sum_{i=1}^n (Y_i - \hat{Y}_i)^2$

低いMSEは、モデルがデータによくフィットしていることを示します。

重回帰分析

重回帰分析は、複数の独立変数を含めた単回帰分析の概念を拡張します。従属変数( $Y$ )と独立変数( $X_1,X_2,...,X_p$ )の関係についての式は次のように書けます。

$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_pX_p + \epsilon$

$Y$ は従属変数
$X_1,X_2,...,X_p$ は独立変数
$\beta_0$ は超平面の切片
$\beta_1,\beta_2,...,\beta_p$ は独立変数の係数
$\epsilon$ は誤差項（ $Y$ の実測値と予測値の差）

行列アプローチ

重回帰分析では、独立変数の係数を推定するために、行列アプローチを使用します。最小二乗推定値は、次の行列方程式を解くことで得られます。

$\boldsymbol{\beta} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}$

$\boldsymbol{\beta}$ は係数( $\beta_0,\beta_1,...,\beta_p$ )を含むベクトル
$\mathbf{X}$ は独立変数の行列であり、各行がデータ点を表し、各列が独立変数を表す
$\mathbf{Y}$ は従属変数の値を含むベクトル

多重共線性の扱い

複数の独立変数が相関している場合、多重共線性が発生します。これは不安定な推定値を導き、独立変数の係数を解釈することが困難になる可能性があります。多重共線性を検出するためには、各独立変数の分散拡大係数（VIF）を計算できます。

$VIF_i = \frac{1}{1 - R_i^2}$

ここで、 $R_i^2$ は $i$ 番目の独立変数を他の独立変数に回帰したときの $R^2$ 値です。VIF値が10を超える場合、多重共線性の程度が高いことを示します。

多重共線性を扱うためには、次の方法があります。

相関する変数の1つを削除する
相関する変数を1つの変数に統合する（平均を取るなど）
リッジ回帰やLasso回帰などの正則化技術を適用する

特徴量選択とスケーリング

重回帰分析では、過剰適合を避け、モデルの解釈性を向上させるために、もっとも関連性の高い独立変数を選択することが重要です。ステップワイズ回帰、再帰的特徴削除、LASSOなどの特徴量選択技術を使用して、もっとも重要な変数を特定することができます。

また、独立変数が異なるスケールを持っている場合、変数の係数を比較することが困難になる場合があります。このような場合、正規化や標準化などの特徴量スケーリング手法を適用して、全ての変数を同じスケールにすることができます。

Pythonによる線形回帰の実装

この章では、PythonとCalifornia Housingデータセットを使用して、単回帰分析と重回帰分析の両方を実装します。このデータセットは回帰タスクの人気のある選択肢であり、scikit-learnライブラリで利用できます。

まず、必要なライブラリをインポートし、scikit-learnライブラリからCalifornia Housingデータセットをロードします。

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# Load the California Housing dataset
dataset = fetch_california_housing()
X = pd.DataFrame(dataset.data, columns=dataset.feature_names)
y = dataset.target

# Display the first few rows of the dataset
print(X.head())

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude
0	8.3252	41.0	6.984127	1.023810	322.0	2.555556	37.88	-122.23
1	8.3014	21.0	6.238137	0.971880	2401.0	2.109842	37.86	-122.22
2	7.2574	52.0	8.288136	1.073446	496.0	2.802260	37.85	-122.24
3	5.6431	52.0	5.817352	1.073059	558.0	2.547945	37.85	-122.25
4	3.8462	52.0	6.281853	1.081081	565.0	2.181467	37.85	-122.25

単回帰分析

まず、特定の地域の中央収入を表すMedInc特徴量を使用して、中央家価格を予測するための単回帰分析を実装します。

データをトレーニングセットとテストセットに分割します。

python

X_simple = X[["MedInc"]]
X_train_simple, X_test_simple, y_train, y_test = train_test_split(X_simple, y, test_size=0.2, random_state=42)

単回帰分析モデルを作成し、トレーニングデータにフィットさせます。

python

simple_lr = LinearRegression()
simple_lr.fit(X_train_simple, y_train)

MSEと $R^2$ スコアを使用して、モデルのパフォーマンスを評価します。

python

y_pred_simple = simple_lr.predict(X_test_simple)
mse_simple = mean_squared_error(y_test, y_pred_simple)
r2_simple = r2_score(y_test, y_pred_simple)

print("Simple Linear Regression - MSE:", mse_simple)
print("Simple Linear Regression - R² Score:", r2_simple)

Simple Linear Regression - MSE: 0.7091157771765549
Simple Linear Regression - R² Score: 0.45885918903846656

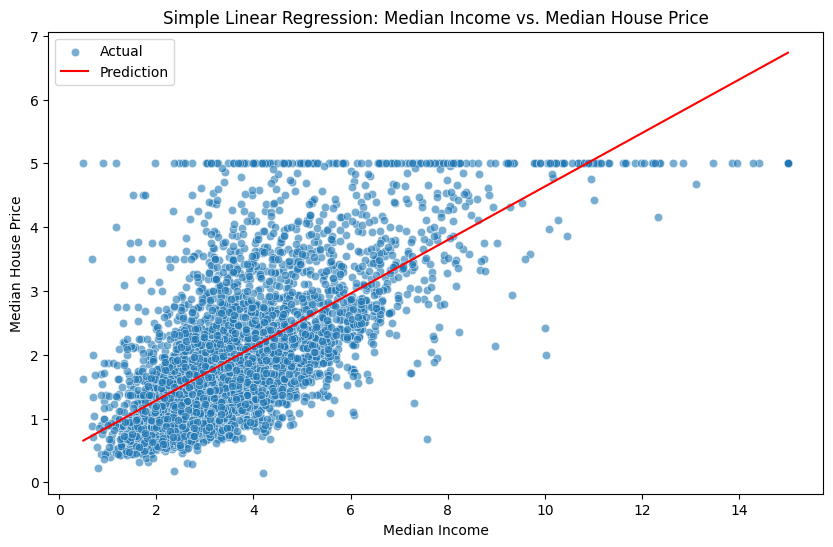
MatplotlibとSeabornを使用して、最適な適合線をプロットします。

python

plt.figure(figsize=(10, 6))
sns.scatterplot(x=X_test_simple["MedInc"], y=y_test, alpha=0.6, label="Actual")
sns.lineplot(x=X_test_simple["MedInc"], y=y_pred_simple, color="red", label="Prediction")
plt.xlabel("Median Income")
plt.ylabel("Median House Price")
plt.title("Simple Linear Regression: Median Income vs. Median House Price")
plt.legend()
plt.show()

Simple linear regression

重回帰分析

次に、データセットの全ての特徴量を使用して、重回帰分析を実装します。

データをトレーニングセットとテストセットに分割します。

python

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

重回帰分析モデルを作成し、トレーニングデータにフィットさせます。

multiple_lr = LinearRegression()
multiple_lr.fit(X_train, y_train)

平均二乗誤差（MSE）と $R^2$ スコアを使用して、モデルのパフォーマンスを評価します。

python

y_pred_multiple = multiple_lr.predict(X_test)
mse_multiple = mean_squared_error(y_test, y_pred_multiple)
r2_multiple = r2_score(y_test, y_pred_multiple)

print("Multiple Linear Regression - MSE:", mse_multiple)
print("Multiple Linear Regression - R² Score:", r2_multiple)

Multiple Linear Regression - MSE: 0.5558915986952444
Multiple Linear Regression - R² Score: 0.5757877060324508

今度は、単回帰分析モデルと重回帰分析モデルのMSEと $R^2$ スコアを比較して、モデルのパフォーマンスを比較します。

python

print("Simple Linear Regression - MSE:", mse_simple)
print("Simple Linear Regression - R² Score:", r2_simple)
print("Multiple Linear Regression - MSE:", mse_multiple)
print("Multiple Linear Regression - R² Score:", r2_multiple)

Simple Linear Regression - MSE: 0.709
Simple Linear Regression - R² Score: 0.459
Multiple Linear Regression - MSE: 0.556
Multiple Linear Regression - R² Score: 0.576

結果に基づいて、重回帰分析モデルの方が一般的にMSEが低く、 $R^2$ スコアが高くなる傾向があります。これは、重回帰分析モデルがデータにより適しており、与えられた特徴量を使用して中央家価格をより正確に予測できることを示しています。