はじめに

いくつかの統計モデルが作られたときに、どの統計モデルが良いモデルと言えるのかについて、1つの指標となるAICについて説明します。

データとモデル

今回は一般化線形モデルの記事で扱ったある架空の植物100個体の種子数データと統計モデルを使用します。

データは次のようになっています。yは個体の種子数、xは個体のサイズ、fは個体の施肥処理の有無（カテゴリ変数）です。

このデータから、次のポアソン回帰モデルが構築されています。

• 種子数がサイズに依存する統計モデル（xモデル）
  • \lambda_i = e^{\beta_1 + \beta_2 x_i}
• 種子数が施肥処理の有無に依存する統計モデル（fモデル）
  • \lambda_i = e^{\beta_1 + \beta_3 d_i}（d_iはダミー変数）
• 種子数がサイズと施肥処理の有無に依存する統計モデル（xfモデル）
  • \lambda_i = e^{\beta_1 + \beta_2 x_i + \beta_3 d_i}

逸脱度

統計モデルのパラメータを最尤推定したときに、観測データへの当てはまりの良さである対数尤度を最大にするようなパラメータを探索しました。

ここで、当てはまりの悪さを示す指標として逸脱度 devianceという指標があります。逸脱度 D は次の式で定義されます。

\log L^* は最大対数尤度です。逸脱度の実態としては、最大対数尤度 \log L^* に-2を掛けているだけになります。

xモデルのパラメータ推定結果のサマリーは次のようになっています。

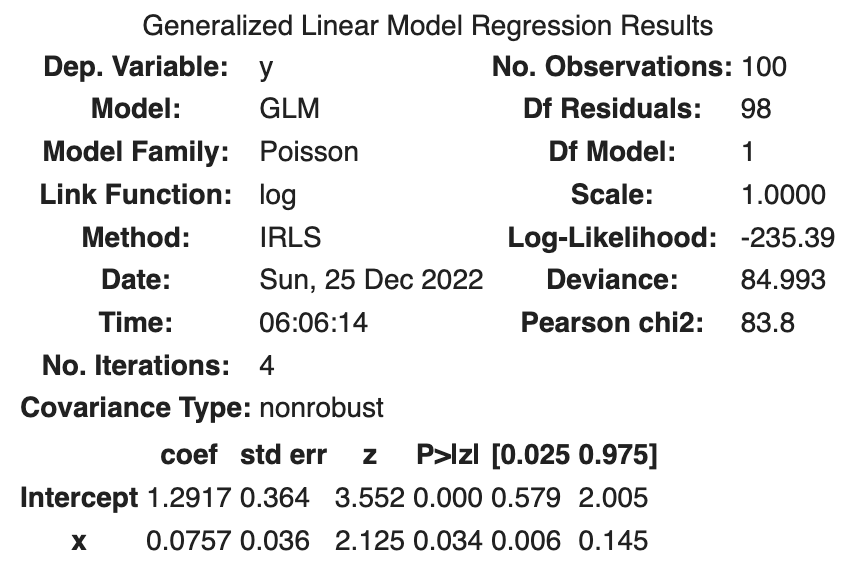
最大対数尤度は-235.39なので逸脱度 D = \log L^*$ は470.78になります。しかし、470.78という数値はサマリーにはなく、代わりにDevianceという数値が示されています。

表示されているDevianceとは、残差逸脱度のことで、次のように定義されます。

D_{min} はフルモデルの逸脱度になります。フルモデルとは、データ数に相当する数のパラメータを使って当てはめたモデルになります。例えば今回のデータ数は100なので100のパラメータを使って当てはめた統計モデルです。つまり、フルモデルは全データを読み上げているだけなので統計モデルとしての価値はありません。ただし、フルモデルは当てはまりの良さ、つまりは対数尤度が最大となり、最小の逸脱度 D_{min} が得られます。

残差逸脱度はフルモデルの逸脱度を基準とする当てはまりの悪さの相対値ということになります。

次に残差逸脱度の最大値を考えます。逸脱度が最大となるモデルは、もっとも当てはまりが悪いモデル、つまり説明変数が組み込まれていないモデルです。このモデルはNullモデルと呼ばれています。

Nullモデルは次のようにして構築することができます。

import statsmodels.api as sm
import statsmodels.formula.api as smf

fit_null = smf.glm('y ~ 1', data=df, family=sm.families.Poisson()).fit()
fit_null.summary()

最大の残差逸脱度 D_{max}は89.507になります。

逸脱度についてまとめると次の表のようになります。

各モデルについてまとめると次のようになります。

パラメータ数が多いモデルほどデータへの当てはまりが良くなることが分かります。

AIC

モデルを複雑にする、つまりモデルのパラメータ数を増やすと最大対数尤度が改善され、観測データへの当てはまりが良くなることが分かりました。しかし、それはたまたま得られた観測データに対して当てはまりが良いだけで、他のデータに対しては全然当てはまらないかもしれません。言い換えると、ある観測データに対して当てはまりは良い一方、別の観測データに対する予測力が低い可能性があります。機械学習の用語で言うと、学習データに対して過学習を引き起こしている可能性があるということになります。

そこで最大対数尤度のバイアス補正によって評価されるAIC（Akaike information criterion）という指標があります。AICは当てはまりの良さではなく予測の良さを重視する指標です。

AICは次の式で表されます。

k は最尤推定したパラメータの数です。k によりモデルの複雑さによるバイアス補正がされています。AICが小さいほど良いモデルになります。

次のコードでAICは簡単に出力されます。

print('null model', fit_null.aic)
print('f model', fit_f.aic)
print('x model', fit_x.aic)

null model 477.2864426185736
f model 479.25451392137364
x model 477.2864426185736

AICを規準とするとxモデルがもっとも良いモデルということになります。

AIC によるモデル選択の注意点

観測データが少ない場合は、真のモデルよりもパラメータ数が少ないモデルの方がAICが小さくなる可能性があります。観測データが少ないため、データから法則性を見つけられないため、シンプルなモデルの方が予測力が高くなる場合があります。

参考

https://kuboweb.github.io/-kubo/ce/IwanamiBook.html
https://eprints.lib.hokudai.ac.jp/dspace/bitstream/2115/49477/4/kubostat2008c.pdf