標準正規分布表とは
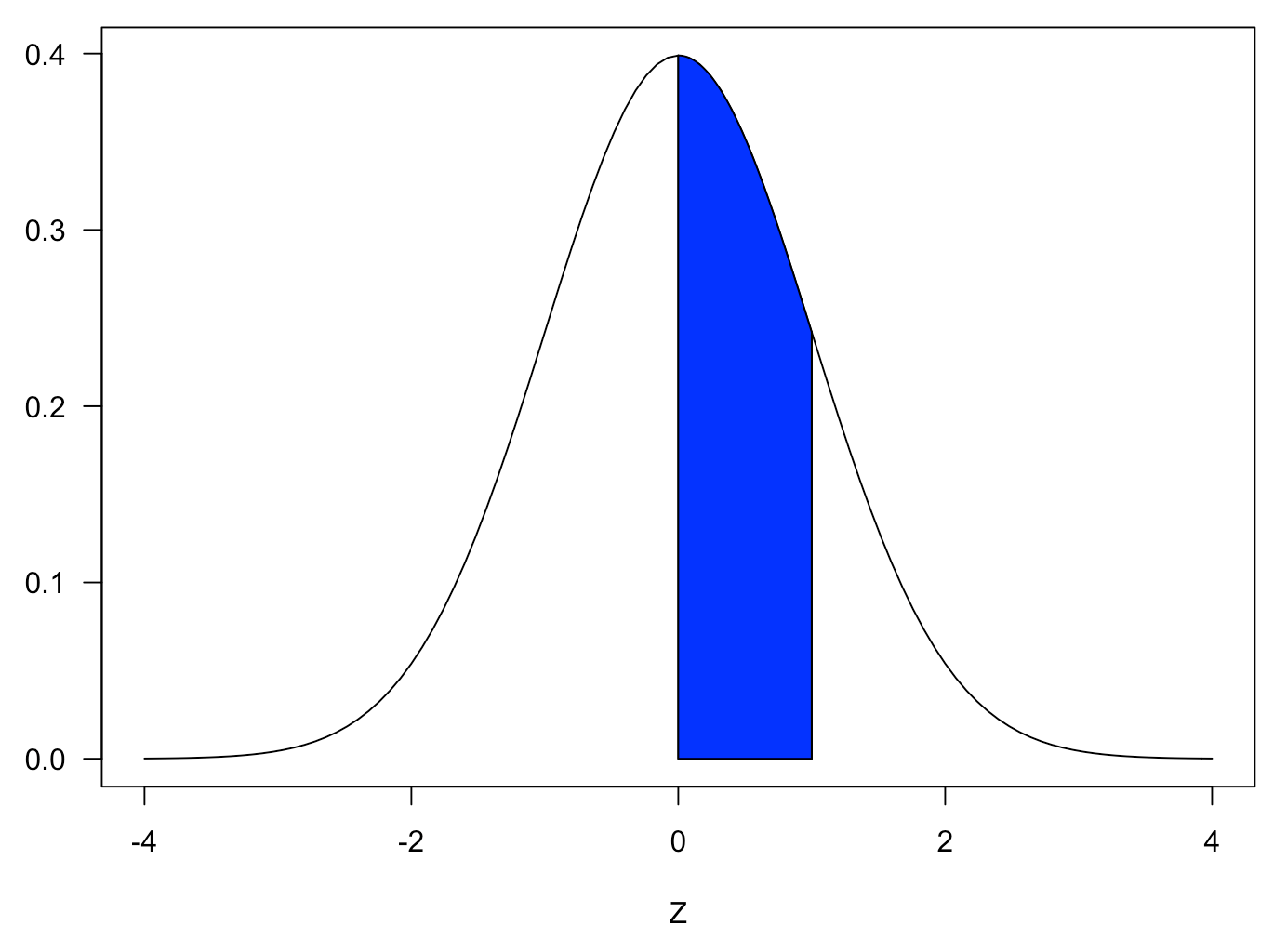
標準正規分布表とは、平均0、分散1の正規分布の面積を計算した表です。標準正規分布表には次のようなグラフと数表が記載されています。
| z | 0 | 0.01 | 0.02 | 0.03 | 0.04 | 0.05 | 0.06 | 0.07 | 0.08 | 0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0.003989 | 0.007978 | 0.011966 | 0.015953 | 0.019939 | 0.023922 | 0.027903 | 0.031881 | 0.035856 |
| 0.1 | 0.039828 | 0.043795 | 0.047758 | 0.051717 | 0.055670 | 0.059618 | 0.063559 | 0.067495 | 0.071424 | 0.075345 |
| 0.2 | 0.079260 | 0.083166 | 0.087064 | 0.090954 | 0.094835 | 0.098706 | 0.102568 | 0.106420 | 0.110261 | 0.114092 |
| 0.3 | 0.117911 | 0.121720 | 0.125516 | 0.129300 | 0.133072 | 0.136831 | 0.140576 | 0.144309 | 0.148027 | 0.151732 |
| 0.4 | 0.155422 | 0.159097 | 0.162757 | 0.166402 | 0.170031 | 0.173645 | 0.177242 | 0.180822 | 0.184386 | 0.187933 |
| 0.5 | 0.191462 | 0.194974 | 0.198468 | 0.201944 | 0.205401 | 0.208840 | 0.212260 | 0.215661 | 0.219043 | 0.222405 |
| 0.6 | 0.225747 | 0.229069 | 0.232371 | 0.235653 | 0.238914 | 0.242154 | 0.245373 | 0.248571 | 0.251748 | 0.254903 |
| 0.7 | 0.258036 | 0.261148 | 0.264238 | 0.267305 | 0.270350 | 0.273373 | 0.276373 | 0.279350 | 0.282305 | 0.285236 |
| 0.8 | 0.288145 | 0.291030 | 0.293892 | 0.296731 | 0.299546 | 0.302337 | 0.305105 | 0.307850 | 0.310570 | 0.313267 |
| 0.9 | 0.315940 | 0.318589 | 0.321214 | 0.323814 | 0.326391 | 0.328944 | 0.331472 | 0.333977 | 0.336457 | 0.338913 |
| 1.0 | 0.341345 | 0.343752 | 0.346136 | 0.348495 | 0.350830 | 0.353141 | 0.355428 | 0.357690 | 0.359929 | 0.362143 |
| 1.1 | 0.364334 | 0.366500 | 0.368643 | 0.370762 | 0.372857 | 0.374928 | 0.376976 | 0.379000 | 0.381000 | 0.382977 |
| 1.2 | 0.384930 | 0.386861 | 0.388768 | 0.390651 | 0.392512 | 0.394350 | 0.396165 | 0.397958 | 0.399727 | 0.401475 |
| 1.3 | 0.403200 | 0.404902 | 0.406582 | 0.408241 | 0.409877 | 0.411492 | 0.413085 | 0.414657 | 0.416207 | 0.417736 |
| 1.4 | 0.419243 | 0.420730 | 0.422196 | 0.423641 | 0.425066 | 0.426471 | 0.427855 | 0.429219 | 0.430563 | 0.431888 |
| 1.5 | 0.433193 | 0.434478 | 0.435745 | 0.436992 | 0.438220 | 0.439429 | 0.440620 | 0.441792 | 0.442947 | 0.444083 |
| 1.6 | 0.445201 | 0.446301 | 0.447384 | 0.448449 | 0.449497 | 0.450529 | 0.451543 | 0.452540 | 0.453521 | 0.454486 |
| 1.7 | 0.455435 | 0.456367 | 0.457284 | 0.458185 | 0.459070 | 0.459941 | 0.460796 | 0.461636 | 0.462462 | 0.463273 |
| 1.8 | 0.464070 | 0.464852 | 0.465620 | 0.466375 | 0.467116 | 0.467843 | 0.468557 | 0.469258 | 0.469946 | 0.470621 |
| 1.9 | 0.471283 | 0.471933 | 0.472571 | 0.473197 | 0.473810 | 0.474412 | 0.475002 | 0.475581 | 0.476148 | 0.476705 |
| 2.0 | 0.477250 | 0.477784 | 0.478308 | 0.478822 | 0.479325 | 0.479818 | 0.480301 | 0.480774 | 0.481237 | 0.481691 |
| 2.1 | 0.482136 | 0.482571 | 0.482997 | 0.483414 | 0.483823 | 0.484222 | 0.484614 | 0.484997 | 0.485371 | 0.485738 |
| 2.2 | 0.486097 | 0.486447 | 0.486791 | 0.487126 | 0.487455 | 0.487776 | 0.488089 | 0.488396 | 0.488696 | 0.488989 |
| 2.3 | 0.489276 | 0.489556 | 0.489830 | 0.490097 | 0.490358 | 0.490613 | 0.490863 | 0.491106 | 0.491344 | 0.491576 |
| 2.4 | 0.491802 | 0.492024 | 0.492240 | 0.492451 | 0.492656 | 0.492857 | 0.493053 | 0.493244 | 0.493431 | 0.493613 |
| 2.5 | 0.493790 | 0.493963 | 0.494132 | 0.494297 | 0.494457 | 0.494614 | 0.494766 | 0.494915 | 0.495060 | 0.495201 |
| 2.6 | 0.495339 | 0.495473 | 0.495604 | 0.495731 | 0.495855 | 0.495975 | 0.496093 | 0.496207 | 0.496319 | 0.496427 |
| 2.7 | 0.496533 | 0.496636 | 0.496736 | 0.496833 | 0.496928 | 0.497020 | 0.497110 | 0.497197 | 0.497282 | 0.497365 |
| 2.8 | 0.497445 | 0.497523 | 0.497599 | 0.497673 | 0.497744 | 0.497814 | 0.497882 | 0.497948 | 0.498012 | 0.498074 |
| 2.9 | 0.498134 | 0.498193 | 0.498250 | 0.498305 | 0.498359 | 0.498411 | 0.498462 | 0.498511 | 0.498559 | 0.498605 |
| 3.0 | 0.498650 | 0.498694 | 0.498736 | 0.498777 | 0.498817 | 0.498856 | 0.498893 | 0.498930 | 0.498965 | 0.498999 |
| 3.1 | 0.499032 | 0.499065 | 0.499096 | 0.499126 | 0.499155 | 0.499184 | 0.499211 | 0.499238 | 0.499264 | 0.499289 |
| 3.2 | 0.499313 | 0.499336 | 0.499359 | 0.499381 | 0.499402 | 0.499423 | 0.499443 | 0.499462 | 0.499481 | 0.499499 |
| 3.3 | 0.499517 | 0.499534 | 0.499550 | 0.499566 | 0.499581 | 0.499596 | 0.499610 | 0.499624 | 0.499638 | 0.499651 |
| 3.4 | 0.499663 | 0.499675 | 0.499687 | 0.499698 | 0.499709 | 0.499720 | 0.499730 | 0.499740 | 0.499749 | 0.499758 |
| 3.5 | 0.499767 | 0.499776 | 0.499784 | 0.499792 | 0.499800 | 0.499807 | 0.499815 | 0.499822 | 0.499828 | 0.499835 |
| 3.6 | 0.499841 | 0.499847 | 0.499853 | 0.499858 | 0.499864 | 0.499869 | 0.499874 | 0.499879 | 0.499883 | 0.499888 |
| 3.7 | 0.499892 | 0.499896 | 0.499900 | 0.499904 | 0.499908 | 0.499912 | 0.499915 | 0.499918 | 0.499922 | 0.499925 |
| 3.8 | 0.499928 | 0.499931 | 0.499933 | 0.499936 | 0.499938 | 0.499941 | 0.499943 | 0.499946 | 0.499948 | 0.499950 |
| 3.9 | 0.499952 | 0.499954 | 0.499956 | 0.499958 | 0.499959 | 0.499961 | 0.499963 | 0.499964 | 0.499966 | 0.499967 |
| 4.0 | 0.499968 | 0.499970 | 0.499971 | 0.499972 | 0.499973 | 0.499974 | 0.499975 | 0.499976 | 0.499977 | 0.499978 |
数表にはグラフの青色の面積を計算した結果が書かれています。グラフの横軸はz値と呼ばれる値になります。
z 値とは
いかなる正規分布であっても、標準化して標準正規分布に変換することができます。z値とは、正規分布を標準化して、データが平均値から標準偏差いくつ分離れているかを示した値になります。
ある正規分布の平均が
標準正規分布表の作成方法
今回はGoogle Sheetsで下図の青色の部分を計算する標準正規分布表を作成します。

まずGoogle SheetsのA列と1行目を次のように埋めます。
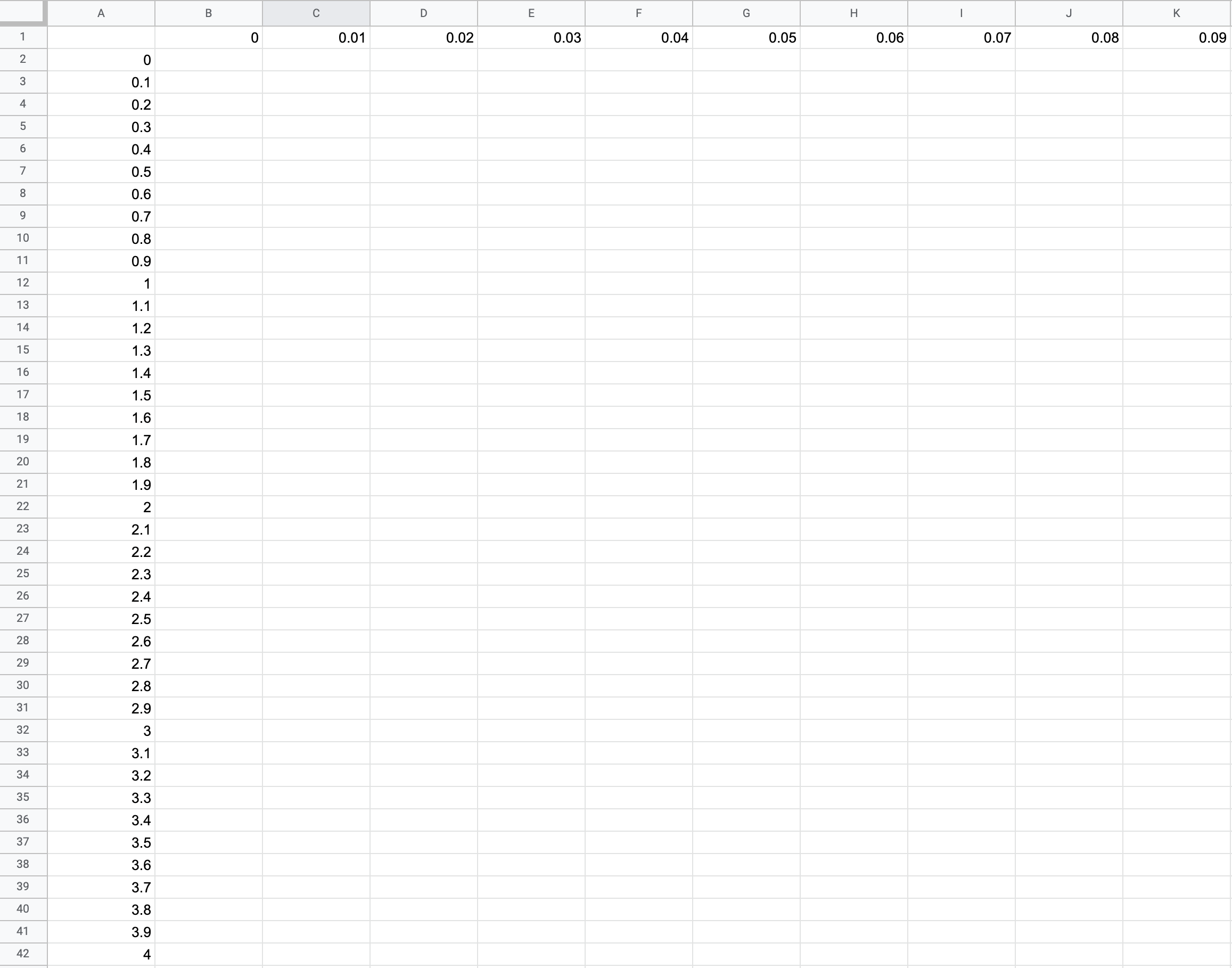
そしてセルB2に関数=NORM.DIST($A2+B$1,0,1,TRUE)-0.5を入力します。
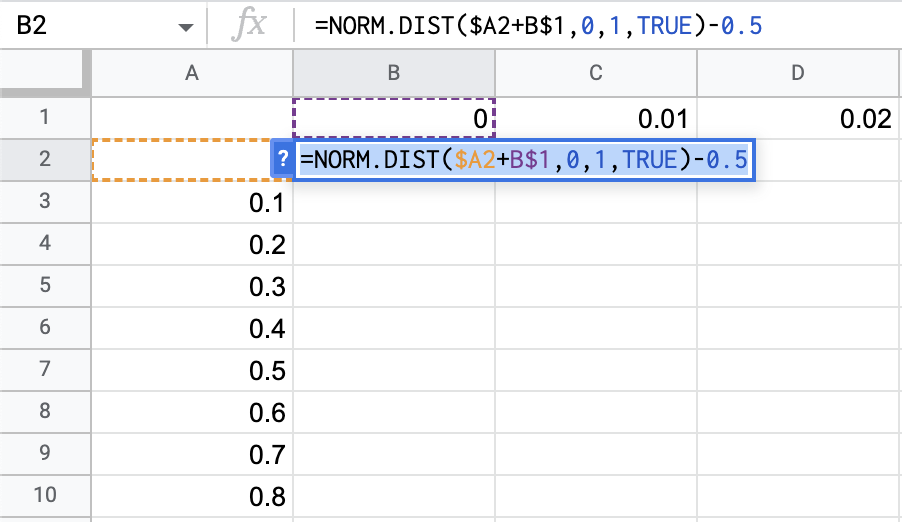
セルB2をドラッグして関数を表全体に反映します。
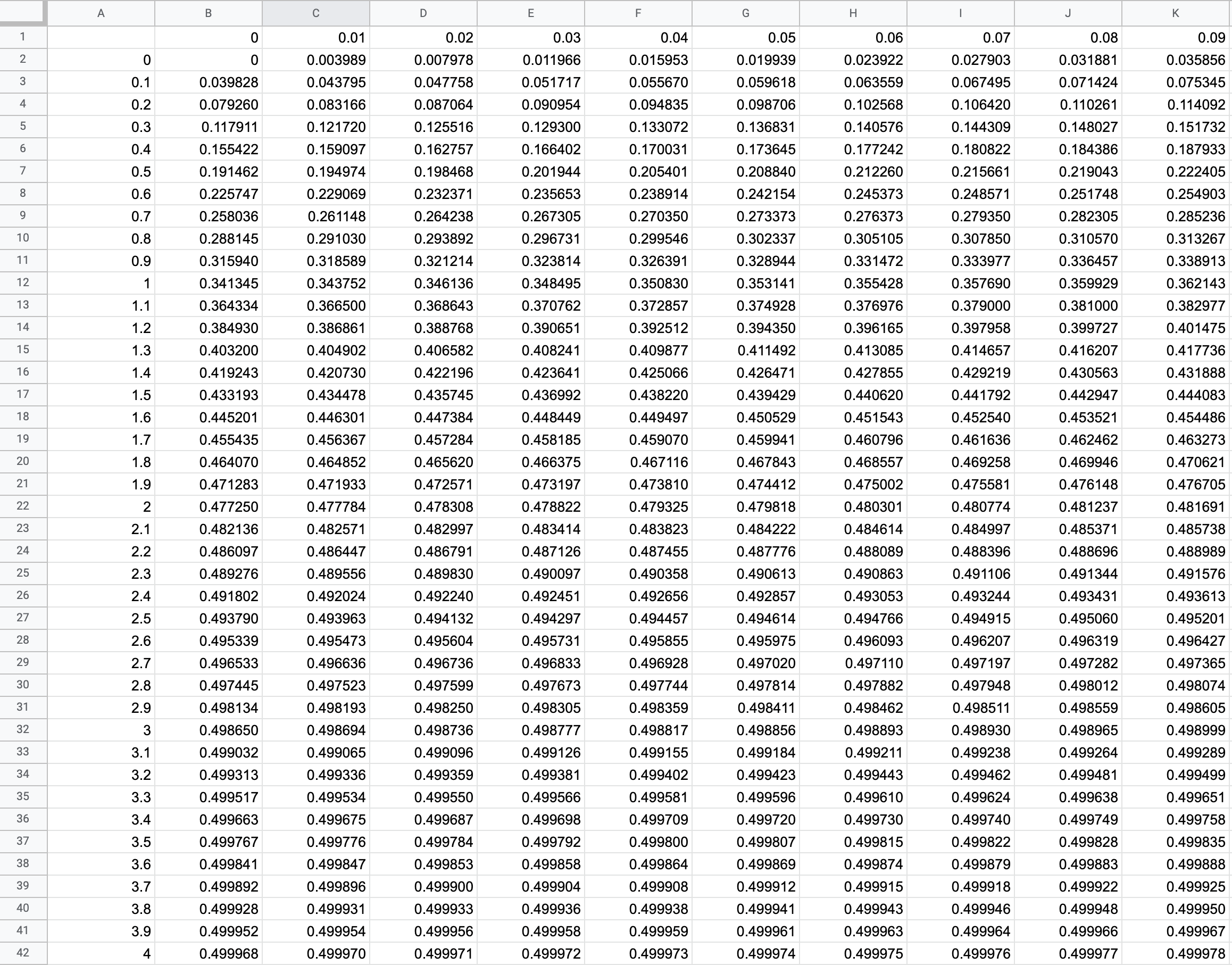
これで標準正規分布表が完成しました。
関数として使用したNORM.DIST()は正規分布の面積を計算する関数で、引数はNORM.DIST(𝑥, 平均, 標準偏差, 関数形)となります。次の緑色の部分を計算しています。
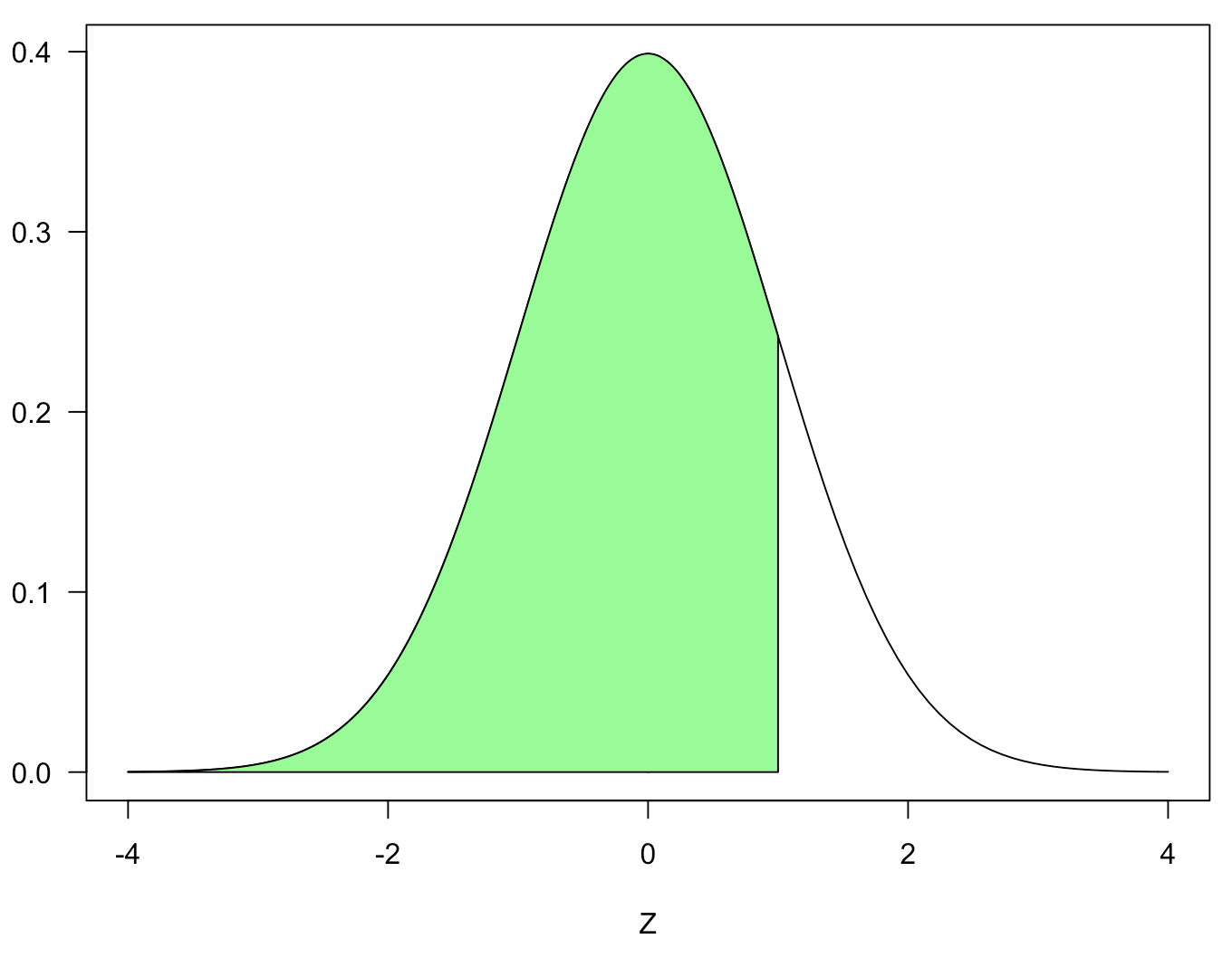
そのため、今回の目標の部分(青色)を算出するには、緑色の部分から下図の黄色の部分を引きます。黄色の部分の面積は0.5になるので、関数としてはNORM.DIST()-0.5になります。
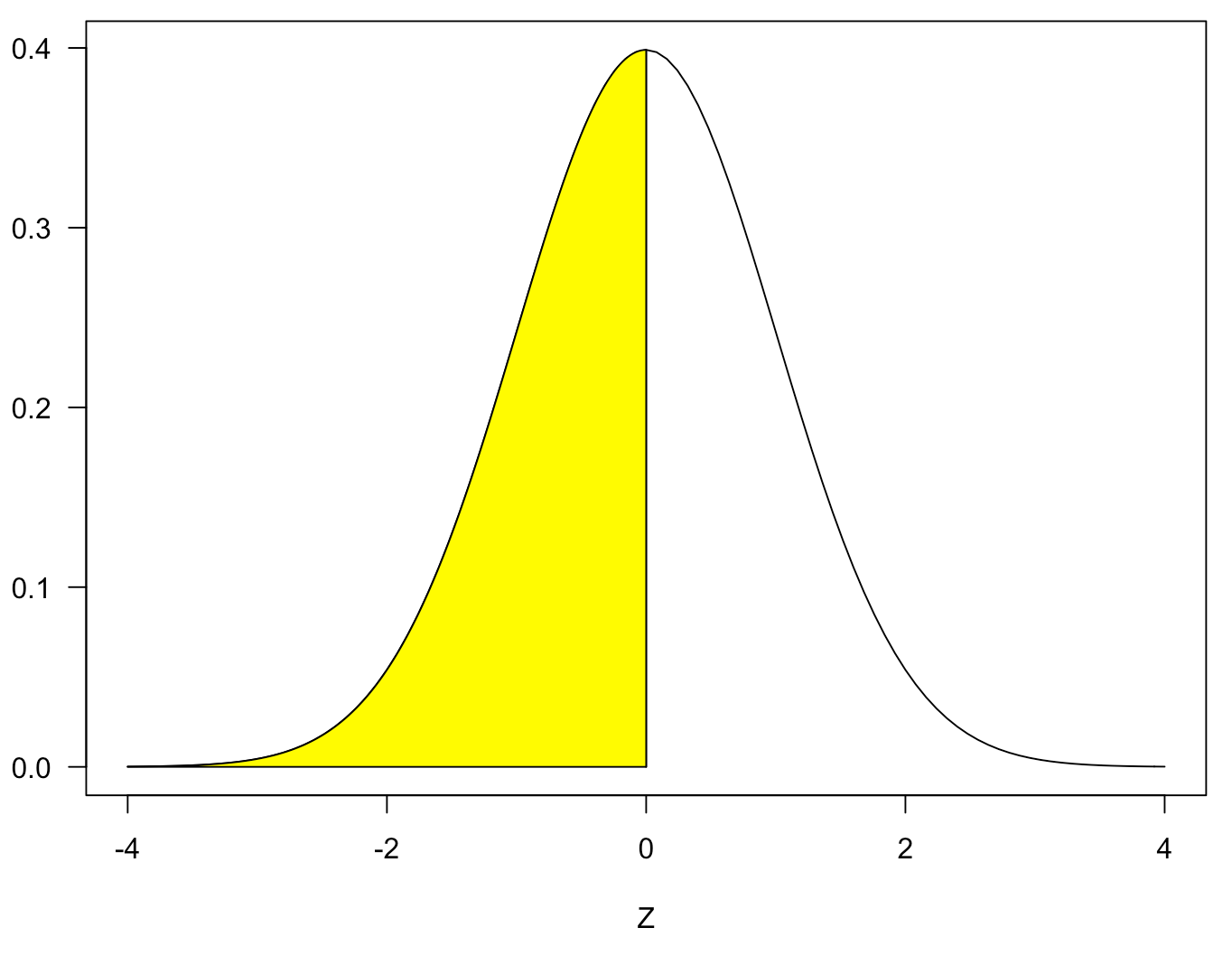
正規分布を描画するために使用したRコードは以下になります。
# green area
curve(dnorm(x), -4, 4, las=1, xlab="Z")
arrows(0,0,0,dnorm(0),length=0)
xvalu <- seq(-4,1,length=200)
dvalu <- dnorm(xvalu)
polygon(c(xvalu, rev(xvalu)), c(rep(0,200), rev(dvalu)),col="palegreen")
# yellow area
curve(dnorm(x), -4, 4, las=1, xlab="Z")
arrows(0,0,0,dnorm(0),length=0)
xvalu <- seq(-4,0,length=200)
dvalu <- dnorm(xvalu)
polygon(c(xvalu, rev(xvalu)), c(rep(0,200), rev(dvalu)),col="yellow")
# blue area
curve(dnorm(x), -4, 4, las=1, xlab="Z")
arrows(0,0,0,dnorm(0),length=0)
xvalu <- seq(0,1,length=200)
dvalu <- dnorm(xvalu)
polygon(c(xvalu, rev(xvalu)), c(rep(0,200), rev(dvalu)),col="blue")
標準正規分布表の見方
標準正規分布表の見方は次の流れになります。
- 一の位と小数第一位の数字の行を見つける。
- 小数第二位の数字の列を見つける。
- 二つが交わるところの数値を読み取る。
例えばz値が1.96のときの値を標準正規分布表から読み取ります。まずは一の位と小数第一位の数字が1.9の行列で見つけます。
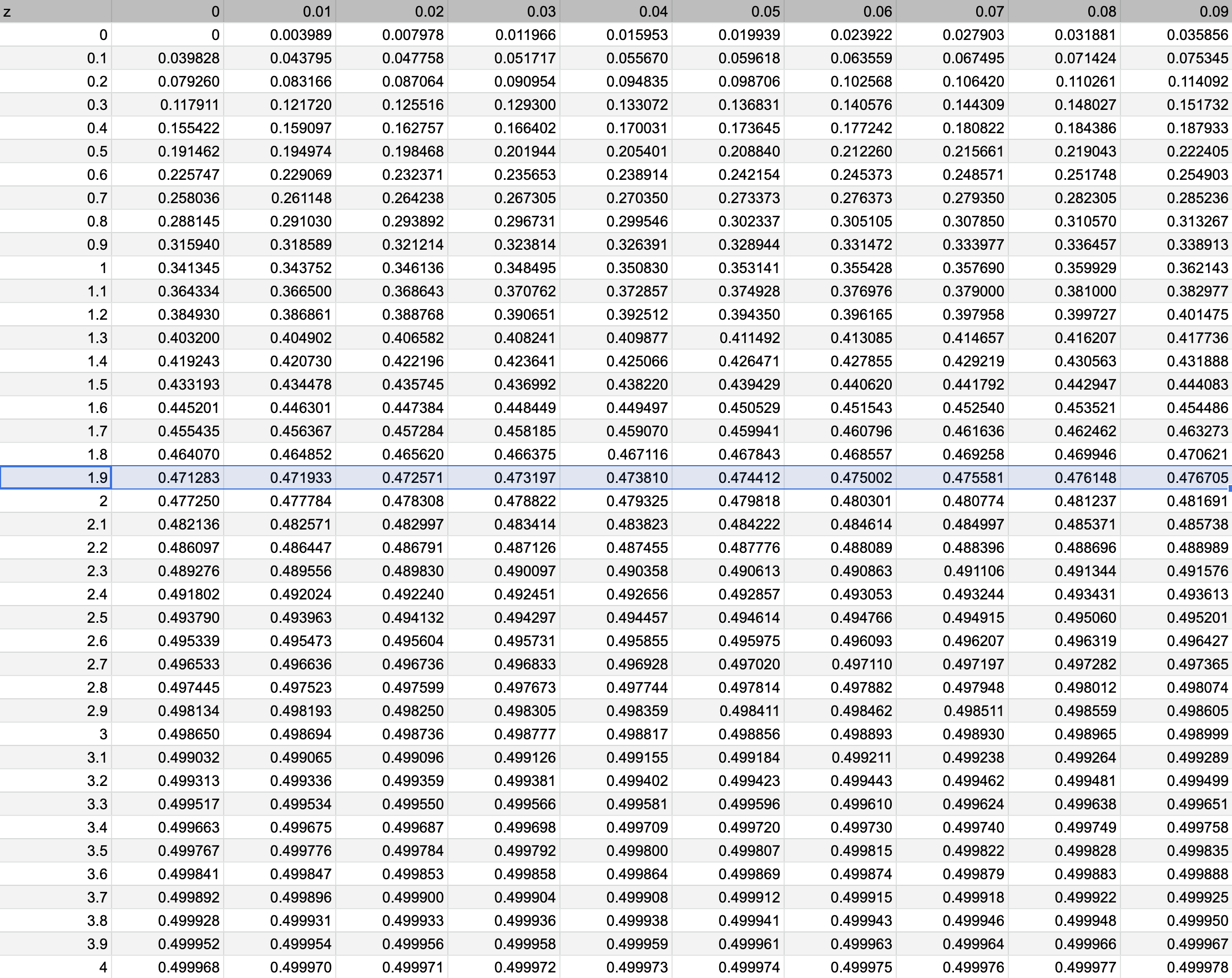
次に小数第二位の数字が0.06の列を見つけます。
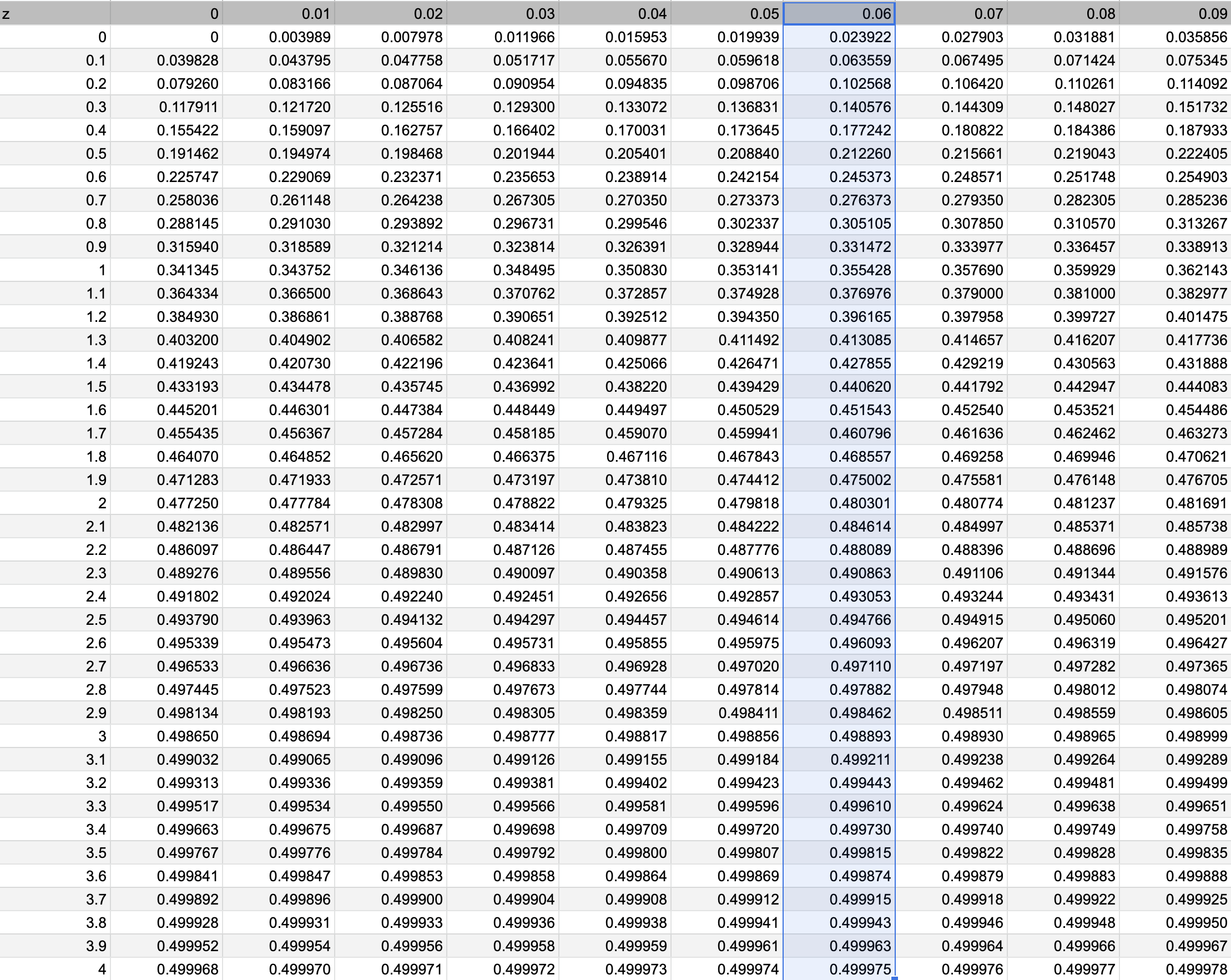
二つが交わるところの数値は0.475002となっています。z=1.96となる確率は47.5%ということが分かります。