因果推論とは

因果推論は、因果関係を理解し分析する方法論です。変数、出来事、または介入の間の因果関係を明らかにし、ある要因が別の要因に及ぼす影響を特定することを目指します。因果推論は、単なる相関関係を超えて、観測可能な現象の基になるメカニズムを明らかにします。

因果推論の根本にあるのは、「もしも〇〇だとどうなるだろう？」や「何の影響があるのか？」といった質問に答えることです。これらの質問は因果性の領域に踏み込み、異なるシナリオでの潜在的な結果を理解しようとします。相関は変数間の関連性に有益な情報を提供できますが、因果推論はさらに一歩進んで、変数間の直接的な影響を特定し数量化します。

因果推論は、単純な相関関係が因果関係を意味するわけではないことを認識しています。2つの変数が関連していると観察されたからといって、片方が他方を引き起こしているとは限りません。交絡要因や隠れた変数、複雑なダイナミクスが影響している可能性があります。これらの課題に対処するために、因果推論は厳密な方法論、統計モデル、実験設計を用いて因果関係を確立します。

因果推論の基礎概念

因果推論の基礎となる概念である交絡変数と反事実について紹介します。

交絡変数

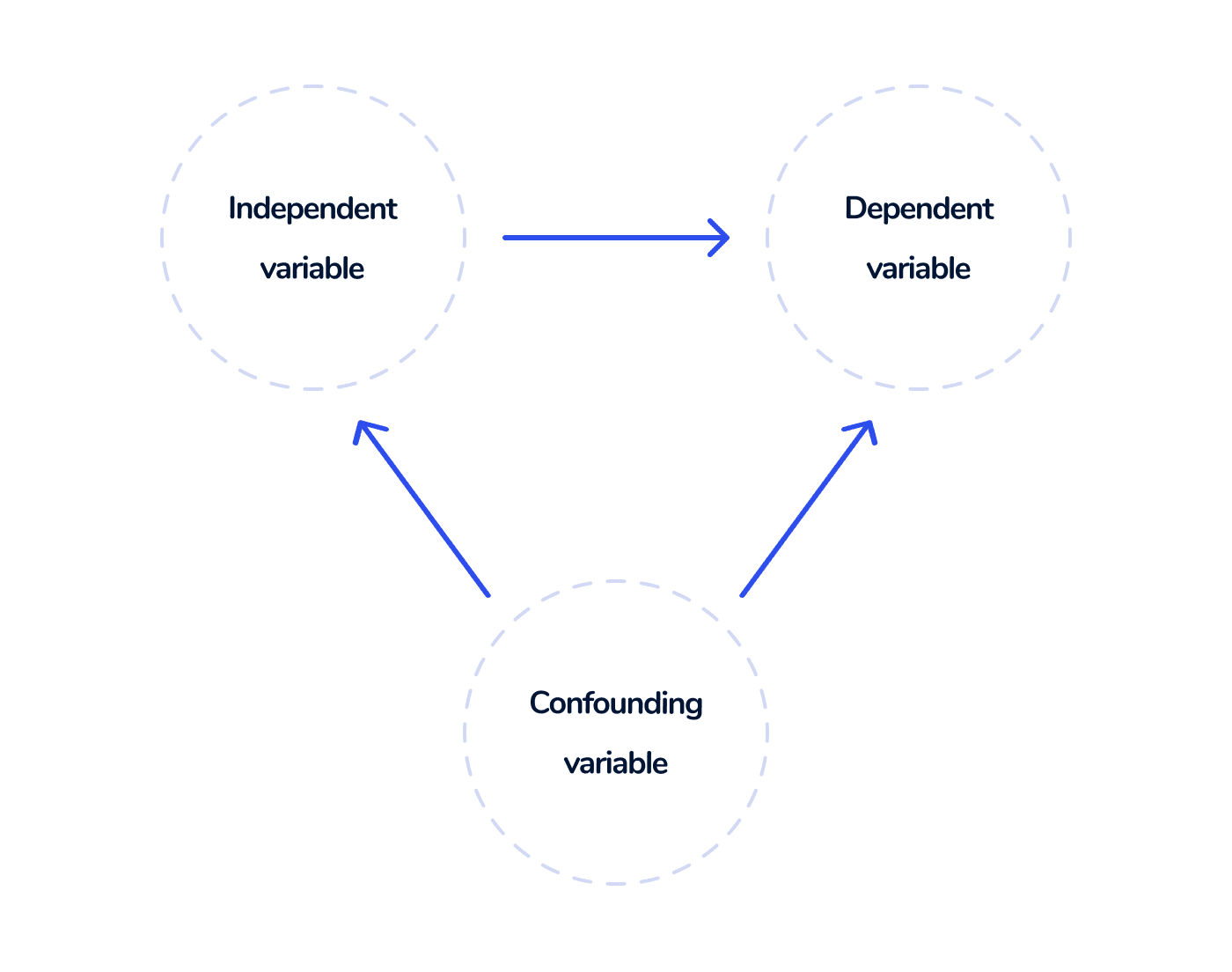
因果推論の領域において、交絡変数は重要な役割を果たします。交絡変数とは、独立変数（処置）と従属変数（結果）の両方と関連している変数のことです。これらの交絡変数はバイアスを導入し、処置と結果の真の関係を曇らせる可能性があります。

Confounding Variable: Easy Guide + Examples

例えば、新しい薬の患者の結果に与える影響を調査する研究を考えてみます。年齢は交絡変数として機能する可能性があります。なぜなら、年齢は薬の投与と患者の健康状態の両方と関連しているからです。年齢が適切に制御されない場合、薬と結果の関係に強い関連性があるように見える誤った印象を与える可能性がありますが、実際には年齢が観察された効果の背後にある要因かもしれません。

交絡変数を制御することは、因果推論において処置と結果の関係を正確に反映させるために重要です。ランダム化や回帰分析などのさまざまな統計的手法や研究デザインが、交絡変数の問題を解決し、因果推論への影響を最小化するために用いられます。

反事実

反事実は、因果推論における基本的な概念です。反事実は、現実には起こらなかった別のシナリオや条件を想像することを含みます。反事実は、もし処置や介入が異なっていた場合や行われなかった場合、どうなるかという質問に答えるのに役立ちます。

反事実の枠組みでは、実際に観察された結果（事実）と、異なるシナリオの下で起こった結果（反事実）を比較します。これらの2つの結果の差を検討することで、処置や介入の因果効果を推定することができます。

しかし、因果推論における重要な課題は、同じ単位に対して同時に事実と反事実の結果を観察することはできないという点です。これを「因果推論の根本的な問題」と呼びます。この課題を克服するために、傾向スコアマッチングや操作変数などのさまざまな技術や統計的手法が用いられ、未観測の反事実の結果を推定します。

反事実によって、異なる処置法、政策、または介入の効果を解明し、関心のある結果に対する因果的な影響を理解することができます。反事実は、単なる関連性を超えて因果関係を明らかにし、根拠と慎重な推論に基づいて因果的な主張を行うための枠組みを提供します。

因果推論の手法

因果関係を明らかにするために厳密に検証され、さまざまな分野で適用されている因果推論の手法について説明します。

ランダム化比較試験（RCT）

ランダム化比較試験（RCT）は因果関係を明確にするためのゴールドスタンダードです。RCTでは、被験者を処置群と対照群にランダムに割り当てることにより、交絡変数の問題を軽減します。ランダムな割り当てにより、処置群と対照群が平均的に比較可能になり、処置の効果を分離することができます。

操作変数法（IV）

操作変数法は、無作為化が不可能な場合に使用される手法です。操作変数とは、処置に影響を与えるが結果には直接的な影響を与えない変数のことを指します。この手法を用いることで、処置の結果への因果効果を分離することができます。

回帰不連続性デザイン（RDD）

回帰不連続性デザイン（RDD）は、処置の割り当てがある閾値を超えるかどうかによって決まる場合に使用されます。閾値の近くでは、閾値を下回る個体と閾値を上回る個体は類似している可能性が高く、処置効果を推定するための自然実験のような状況が生まれます。

差分の差（DID）

差分の差（DID）は、処置（政策変更や新しいプログラムなど）の時間的な効果を計算する統計技術です。処置を受けたグループと受けていないグループの間で、処置前後の結果の変化を比較します。この手法では、処置がなかった場合、2つのグループで時間の経過に伴う傾向が同じであると仮定します。

傾向スコアマッチング

傾向スコアマッチングは、処置の効果を推定するために、処置を受けた単位と似た特性を持つ未処置の単位を対応させる手法です。傾向スコアは通常、ロジスティック回帰を用いて推定されます。

因果グラフと有向非巡回グラフ（DAG）

因果グラフ、特に有向非巡回グラフ（DAG）、は変数間の因果関係を視覚的に表現するものです。DAGでは、ノードが変数を表し、ノード間の有向エッジが因果関係を表します。DAGは交絡、選択バイアス、因果分析の複雑さなどについての考察手段を提供します。

因果木と因果フォレスト

これらは因果推論のために設計された現代的な機械学習手法です。因果木は、標準的な決定木とは異なり、結果を直接予測するのではなく、処置効果の差異を特定するために特徴量を分割します。因果フォレストは、因果木のアンサンブルに基づいて予測を行い、因果効果の推定の堅牢性と精度を向上させます。

さまざまな分野での因果推論の応用

因果推論は幅広い分野で深い具体的な影響を持ち、情報を基にした意思決定や洞察の生成のための基礎となっています。以下では、いくつかの応用例を紹介します。

• 医療と流行病学
  因果推論は臨床試験において処置や介入の効果を推定するために重要です。ランダム化比較試験などの手法を用いて、新薬や処置法の因果効果を推定することで、患者ケアの重要な進歩が実現されます。流行病学では、因果推論は疾病の広がりや公衛の介入の効果、リスクファクターの影響などを理解するために重要な役割を果たします。

• 経済学と社会科学
  経済学者は因果推論を使用して、財政政策の影響を推定し、市場の行動を理解し、経済的なショックの結果を予測します。社会科学では、教育、社会プログラム、政策などのさまざまな要因が所得、犯罪、社会的流動性などの結果に与える影響を研究するために使用されます。

• テクノロジー業界
  テクノロジー業界では、企業は因果推論を使用して、アルゴリズムやユーザーインターフェース、サービス提供などの製品の変更がもたらす影響を評価します。広告効果を売上に与える影響を評価し、ユーザーの行動に基づいて製品の特徴を最適化し、パーソナライゼーション戦略を向上させるためにも因果推論が活用されます。

• 公共政策
  公共政策はしばしば社会的な結果を改善することを目的とした介入を含みます。因果推論は政策立案者が介入の予想される効果を理解するのに役立ち、異なる政策を比較し、もっとも効果的な影響を持つ政策を選択することができます。

• 人工知能
  AIシステムがますます複雑になるにつれて、これらのシステム内の因果関係を理解することが重要となります。因果推論はこれらの関係を探求するためのツールを提供し、システムの設計の改善、予測能力の向上、より信頼性のある意思決定システムの構築を支援します。