2022-08-01

決定木とは

Machine Learning

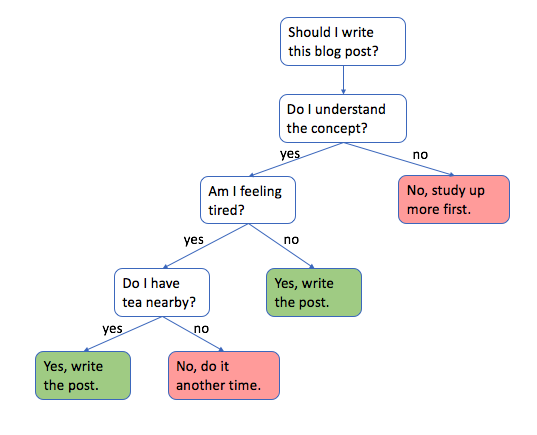
Decision Tree

sklearn

決定木とは

決定木は、広範な分類や回帰問題を解決するために使用される強力な予測モデリングツールです。シンプルでありながら効果的であり、ビジュアルな性質により結果の解釈と伝達が容易になっています。

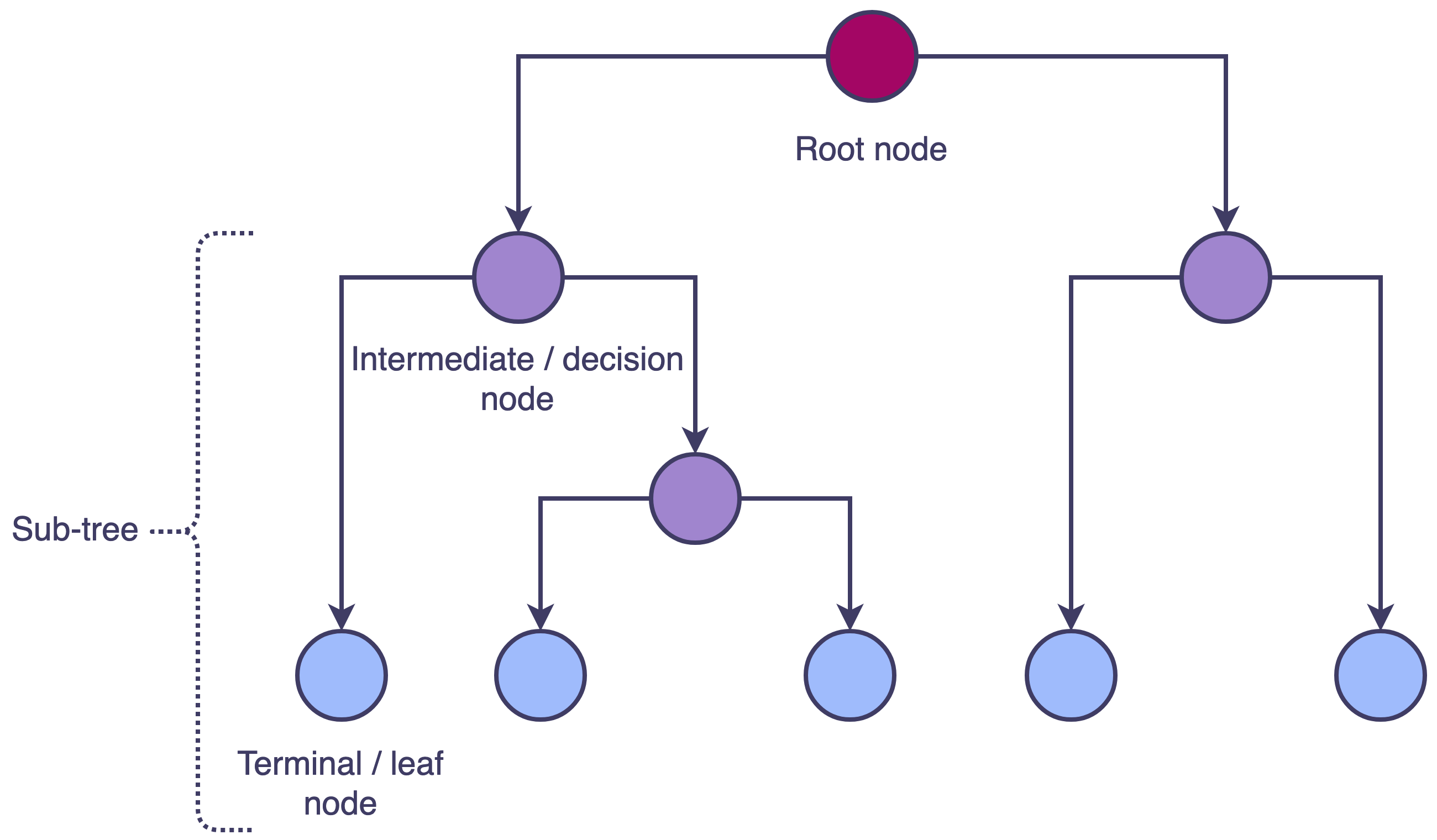
決定木はフローチャートのような構造で、内部ノードが特徴や属性を表し、枝が決定規則を表し、葉ノードが結果や決定を表します。決定木は、Recursive Binary Splitting（再帰的な二分割）というプロセスを通じて構築されます。これには、データセットを分割する最適な属性を選択し、結果のサブセットで再帰的にプロセスを繰り返すことが含まれます。そして、特定の停止基準が満たされるまでこのプロセスが繰り返されます。

Decision trees.

決定木は、金融、医療、マーケティング、詐欺検知などのさまざまなアプリケーションで使用されます。決定木の構築、解釈、評価を理解することにより、データに隠れたパターンやトレンドに基づいて情報を得ることができます。

決定木の構築

この章では、Recursive Binary Splittingの基本概念から始まり、最適な分割の選択やツリーの剪定など、より高度な技術に進んで、決定木の構築プロセスについて探求します。ジニ指数やエントロピーなどのさまざまな不純度測定方法について説明し、それらがツリー構築プロセスに与える影響を説明します。

Recursive Binary Splitting

Recursive Binary Splittingは、決定木を構築するために主に使用される方法です。このプロセスは、入力特徴の値に基づいてデータセットをサブセットに分割することを含みます。全データセットを含むルートノードから始まり、属性と閾値を選択してデータを2つの子ノードに再帰的に分割します。このプロセスは、停止基準が満たされるまで、各子ノードに対して再帰的に繰り返され、決定ノードと葉ノードで構成されたツリー構造が得られます。

Tree splitting
An introduction to decision tree theory

最適な分割の選択

決定木の品質は、データを分割するために使用される属性や閾値の選択に強く依存します。最適な分割を選択するには、その分割によって得られた子ノードの不純度を測定する必要があります。目的は、子ノードの不純度を最小化し、分割によって得られるInformation Gainを最大化することです。

Information Gain

Information Gainは、決定木において各ノードでデータを分割するための最適な属性を決定するために使用される、重要な概念の一つです。特定の属性に基づいてデータを分割した後の不確実性やランダム性の減少を測定します。Information Gainは、データセット内の不純物や無秩序の度合いを測定するエントロピーを使用して計算されます。

Information Gainを計算するためには、親ノードのエントロピーから分割後の子ノードの重み付き平均エントロピーを引きます。そのノードでもっともInformation Gainの高い属性が分割属性として選択されます。このプロセスは、木が完全に成長するまで各ノードで繰り返されます。

Information Gain = 親ノードのエントロピー - 子ノードの重み付き平均エントロピー

IG(S, A) = H(S) - \sum_{v \in A} \frac{|S_v|}{|S|} H(S_v)

ここで、 $IG(S, A)$ は属性 $A$ のInformation Gainであり、 $H(S)$ はデータセット $S$ のエントロピー、 $H(S_v)$ は部分集合 $S_v$ のエントロピーです。

エントロピー

エントロピーは、決定木や情報理論の文脈で主に使用されるデータセットの不純物や無秩序の度合いを測定する指標です。データセット内のクラスラベルの分布に関連する不確実性やランダム性を定量化します。決定木では、エントロピーはInformation Gainを計算するために使用され、さらにデータを分割するための最適な属性を決定するのに役立ちます。

エントロピーは、次の式を使用して計算されます。

Entropy(S) = - \sum_{i=1}^{c} p(i) * log_2(p(i))

ここで、 $Entropy(S)$ はデータセット $S$ のエントロピーであり、 $c$ はクラス数、 $p(i)$ はクラス $i$ に属するインスタンスの確率です。エントロピーは、クラス数が $c$ である場合、0から $log_2(c)$ の範囲で変動します。エントロピーが低いほど、より均質なデータセットを示し、高いほど、より混合されたデータセットを示します。決定木では、各ノードでエントロピーを最小化することを目標としており、これによりクラスの明確な分離とより正確な予測が可能になります。

ジニ指数

ジニ指数は、決定木においてデータを分割するための最適な属性を決定するために使用される、不純物や無秩序の度合いを測定する別の指標です。Information Gainと同様に、分割にもっとも有益な属性を特定するのに役立ちます。

ジニ指数は、0から1の範囲で変動し、0は完全な純度（ノード内の全てのインスタンスが1つのクラスに属する）を示し、1は最大の不純度（インスタンスが全てのクラスに均等に分布している）を示します。特定のノードでもっとも低いジニ指数を持つ属性が分割属性として選択されます。

Gini(S) = 1 - \sum_{i=1}^{c} p(i)^2

ここで、 $Gini(S)$ はデータセット $S$ のジニ指数であり、 $c$ はクラス数、 $p(i)$ はクラス $i$ に属するインスタンスの確率です。

ツリーの剪定

決定木は時に肥大化してしまい、過学習を引き起こすことがあります。これは、ツリーがトレーニングデータにはうまく機能するが、新しい未知のデータにはうまく機能しない状態を意味します。剪定は、ツリーのサイズを縮小し、過学習を緩和するための技術です。主な剪定方法には、プレ剪定とポスト剪定があります。

プレ剪定
プレ剪定は、ツリーが完全に成長する前に停止基準を設定することを含みます。例えば、ツリーの最大深度を制限するか、葉ノード内の最小サンプル数を要求することなどです。
ポスト剪定
ポスト剪定は、ツリーを完全に成長させた後、予測精度に寄与しない枝を反復的に削除することを含みます。もっとも一般的なポスト剪定技術は、誤り率とツリーの複雑さをバランスするコスト複雑度剪定です。

Pythonによる決定木の実装

この章では、機械学習ライブラリScikit-learnを使用してPythonで決定木分類器を実装する方法を示します。多クラス分類問題であるアヤメのデータセットを例に説明します。

データの準備

決定木を構築する前に、データセットを準備することが重要です。このステップには、データの読み込み、トレーニングセットとテストセットに分割すること、欠損値やカテゴリカル変数の処理、特徴量のスケーリングなどが含まれます。

python

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.datasets import load_iris

# Load dataset
iris = load_iris()
X = iris.data
y = iris.target

# Split data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

モデルの定義

次に、Scikit-learnのDecisionTreeClassifierクラスを使用して決定木モデルを定義します。DecisionTreeClassifierクラスを使用することで、ツリーの成長や構造を制御するさまざまなハイパーパラメータを設定することができます。

python

from sklearn.tree import DecisionTreeClassifier

# Define model
dtree = DecisionTreeClassifier(
  criterion='gini',
  max_depth=None,
  min_samples_split=2,
  min_samples_leaf=1,
  random_state=42
)

以下に、主要なハイパーパラメータの簡単な説明を示します。

criterion
ノードの不純度を測定するための基準。ジニ係数の場合は'gini'、エントロピーの場合は'entropy'が使用できます。デフォルト値は'gini'です。
max_depth
ツリーの最大深度。Noneに設定すると、全ての葉が純粋であるか、min_samples_split未満のサンプルを含む場合に、ツリーが拡大します。最大の深度を設定することで、過学習を防ぐことができます。
min_samples_split
内部ノードを分割するために必要な最小サンプル数。この値よりも少ないサンプルを持つ場合、ノードは分割されず、ツリーの成長が停止します。デフォルト値は2です。
min_samples_leaf
リーフノードに必要な最小サンプル数。分割が検討されるのは、左右の枝の少なくともmin_samples_leaf個のサンプルが残る場合のみです。このハイパーパラメータは、ツリーが過剰に特定の葉ノードを作成しないようにすることで、過学習を防ぐのに役立ちます。デフォルト値は1です。
random_state
アルゴリズムで使用される乱数生成器のシード。ランダム状態を設定することで、決定木モデルを再現可能にすることができます。Noneに設定すると、分割プロセスのランダム性により、モデルの結果が実行ごとに異なる可能性があります。

モデルのトレーニング

次に、トレーニングデータ上で決定木モデルをトレーニングします。

python

# Train model
dtree.fit(X_train, y_train)

予測

トレーニングされた決定木モデルを使用して、テストデータのクラスラベルを予測し、精度、適合率、再現率、F1スコアなどのメトリックを使用してモデルの性能を評価します。

python

from sklearn.metrics import classification_report, accuracy_score

# Predict
y_pred = dtree.predict(X_test)

# Evaluate model performance
print("Accuracy:", accuracy_score(y_test, y_pred))
print(classification_report(y_test, y_pred))

Accuracy: 1.0
              precision    recall  f1-score   support

           0       1.00      1.00      1.00        19
           1       1.00      1.00      1.00        13
           2       1.00      1.00      1.00        13

    accuracy                           1.00        45
   macro avg       1.00      1.00      1.00        45
weighted avg       1.00      1.00      1.00        45

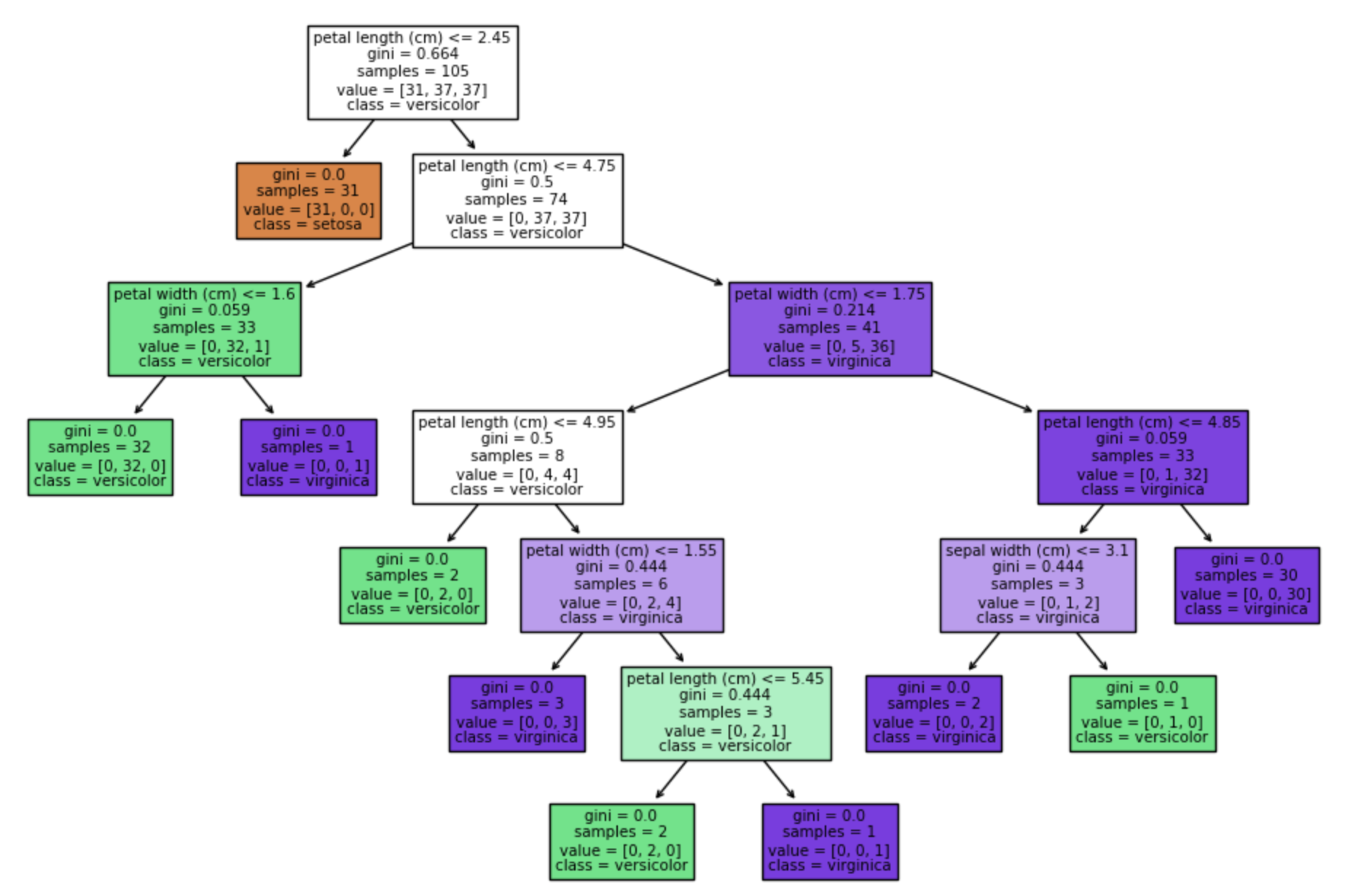
決定木の可視化

決定木を可視化することで、モデルが予測をどのように行っているかを理解し、解釈性を向上させることができます。Scikit-learnのplot_tree関数を使用して、決定木のグラフィカルな表現を作成できます。

python

import matplotlib.pyplot as plt
from sklearn.tree import plot_tree

# Visualize decision tree
plt.figure(figsize=(12, 8))
plot_tree(dtree, filled=True, feature_names=iris.feature_names, class_names=iris.target_names)
plt.show()