2022-04-29

回帰不連続性デザイン（RDD）

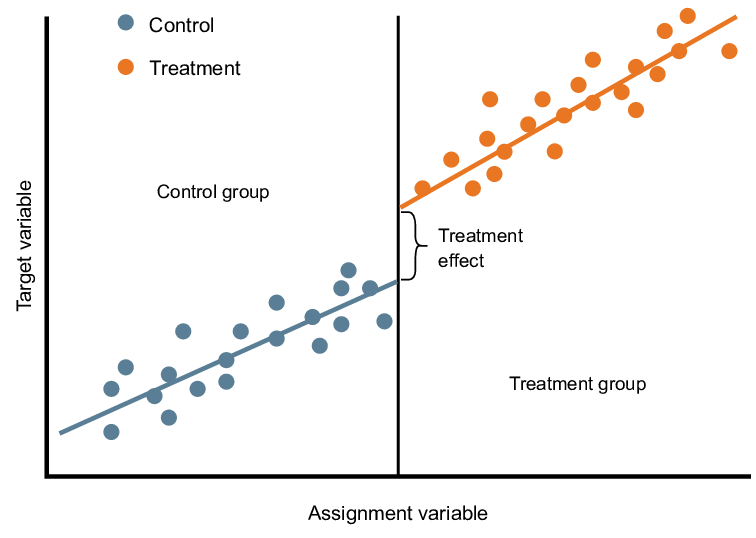
回帰不連続性デザイン（RDD）とは

回帰不連続性デザイン（RDD）は、倫理的、実践的、その他の理由により、グループへの無作為な割り当てが不可能な場合に、介入や処置の因果効果を推定するための研究方法です。RDDは、連続的な測定可能な割り当て変数に基づく閾値ルールや切れ目ルールによって処置や介入が割り当てられるという特定の非無作為な割り当て形態を利用します。

アイデアは非常にシンプルです。割り当て変数（強制変数とも呼ばれる）のスコアがある閾値以上または以下である場合、その個人は特定の処置群または対照群に割り当てられます。例えば、GPAに基づいて奨学金の対象者を決定する、地域の社会経済的状況に基づいてどの学校に追加の資金を提供するかを決めるなどです。

RDDの特に強力な点は、準実験的な環境で介入の因果効果を推定できることです。つまり、処置への割り当てが無作為ではなくても、RDDの設計は少なくとも閾値の周りの局所的な領域では、ランダム化実験の特性を模倣することができます。これは、閾値のすぐ上とすぐ下の単位が、処置の状態を除いて非常に類似しうるためです。したがって、閾値での結果の不連続なジャンプは、処置の因果効果に帰属することができます。

RDD
An illustration explaining the Regression Discontinuity Design model, and how the average treatment effect is estimated.

RDDの仮定

RDDの妥当性は、満たされる必要のあるいくつかの主要な仮定に大きく依存します。これらの仮定の違反は、因果効果のバイアスのある推定値をもたらす可能性があります。

連続性

RDDでもっとも重要な仮定は、処置がない場合の潜在的な結果の連続性です。つまり、処置がない場合において、割り当て変数と結果の間の機能的な関係は、閾値点でスムーズでなければなりません。閾値でのこの関係に処置によるもの以外のジャンプがあってはなりません。この仮定は重要であり、RDDにおける局所比較に基づいて処置効果を推定するための基盤となります。

局所性

2番目の仮定である局所性は、局所的な無作為化または局所的な類似性の原則に基づいています。これは、閾値に近い単位同士の類似性が、それよりも遠くにある単位と比べて高いという仮定です。基本的には、閾値の周りで「ミニ実験」が作成され、閾値のすぐ下とすぐ上の単位がそれぞれ対照群と処置群として機能します。この仮定が成立すれば、これらの群間の平均結果の差は処置効果に帰属できます。

操作不可能性

この仮定は、個人や単位が割り当て変数を正確に操作して処置を保証することができないことを保証します。言い換えれば、閾値の周りにはある程度のランダム性が存在し、単位が自分の処置ステータスを保証することを防ぐ必要があります。この条件が違反されると、閾値のすぐ上と下の単位が基本的に異なる可能性があり、推定される処置効果に系統的なバイアスが導入される可能性があります。

無関連性

最後の仮定である無関連性仮定は、閾値が処置割当に影響を与える以外の潜在的な結果に対しては無関係であるという仮定です。つまり、閾値が処置以外の理由で引き起こされる場合、処置効果の推定値に対してバイアスが生じる可能性があります。

RDDによる因果効果の導出

RDDの主な魅力の一つは、処置割当がランダムではなく、閾値ルールに基づいて行われる設定での因果効果を推定できる能力です。

因果効果の推定

RDDは、割り当て変数の閾値での不連続性を利用して処置の因果効果を推定します。アイデアは、閾値のすぐ下とすぐ上の単位は、処置ステータスを除いてほぼ同一であり、閾値で処置の状態が変わるという点です。したがって、処置の因果効果は、閾値での平均結果のジャンプとして推定されます。

数学的には、単位 $i$ の潜在的な結果を処置ステータス $w$ の下で $Y_i(w)$ と表記することができます。観測された結果 $Y_i$ は次のように表されます。

Y_i = W_iY_i(1) + (1 - W_i)Y_i(0)

ここで、 $W_i$ は単位 $i$ の実際の処置ステータスであり、割り当て変数 $X_i$ が閾値 $c$ を上回る場合は1、それ以外の場合は0となります。

閾値での局所平均処置効果（LATE）は、閾値の右側（閾値を上回る）と左側（閾値を下回る）からの期待値を比較することで次のように表されます。

LATE = E[Y_i(1) - Y_i(0) | X_i = c]= E[Y_i | X_i = c^+]- E[Y_i | X_i = c^-]

ここで、 $c^+$ と $c^-$ はそれぞれ右側（閾値を上回る）と左側（閾値を下回る）からの極限を示します。

方法と戦略

RDDにおいてLATEを推定するためのさまざまな戦略と方法があります。これらは通常、処置群と対照群それぞれに別々の回帰モデルを適用し、閾値での予測される結果を比較することによって行われます。

パラメトリック手法

パラメトリック手法では、閾値の両側でデータに対してパラメトリック回帰モデルを適用します。簡単な線形回帰モデルは次のように表されます。

Y_i = a + bX_i + cW_i + d(X_i - c)W_i + e_i

ここで、 $(X_i - c)W_i$ は閾値の両側で異なる傾きを許容するための交互作用項であり、 $e_i$ はランダムな誤差項です。

閾値での処置の因果効果は、回帰直線のジャンプを捉える係数 $c$ によって推定されます。

ノンパラメトリック手法

一方、ノンパラメトリック手法では、割り当て変数と結果の関係に対して関数形を仮定しません。代わりに、局所的な多項式回帰やカーネル回帰を使用して、閾値の下と上での予測される結果を推定します。

RDDの例

RDDの例として、学生の学業成績向上を目指す教育プログラムの架空の事例研究を考えてみます。

背景

アメリカのある学区では、学生の学業成績向上を支援するための奨学金プログラムを導入しました。このプログラムは、学生の成績ポイント平均（GPA）がある閾値を下回る場合に、無料の家庭教師や教材などの追加の学術的なリソースを提供します。この場合、GPAの閾値は2.5と設定されています。GPAがこの閾値を下回る学生は、プログラムの対象となります。

教育研究者として、このプログラムが学生の学業成績に与える因果効果を推定することに興味があります。具体的には、学年ごとのGPAの変化を指標として、このプログラムの効果を推定したいと考えています。