操作変数とは

操作変数は、統計的分析において一つの変数が他の変数に与える因果効果を分離するために使用されるツールです。操作変数は、回帰分析における内生性の問題を制御するために使用される第三の変数です。内生的説明変数と誤差項との間に相関がある場合、操作変数はこの相関を制御するために使用されます。この相関は、通常、省略された変数、同時性、または測定誤差によって生じます。

概念を説明するために例を考えてみます。例えば、勉強時間が学生の成績に与える効果を研究しているとします。勉強時間と成績の両方に影響を与える、例えば持って生まれた能力といった観測されない変数が存在する場合、独立変数である勉強時間と誤差項との間に相関が生じます。可能な操作変数として、学生の自宅から図書館までの距離が考えられます。この変数は学生が勉強する時間に影響を与える可能性がありますが、学生の成績に直接的に関連しているわけではありません（勉強時間への影響を通じてのみ関連しています）。

操作変数の特定方法

適切な操作変数を特定することは、任意の因果分析において重要なステップであり、おそらくもっとも難しいステップの一つです。操作変数の選択は一般的に理論的な推論と実践的な考慮に基づいています。操作変数が満たす必要な基本的な条件は次の通りです。

• 操作変数は内生的な説明変数と相関している必要があります。これを関連性の条件とも呼びます。この相関は重要であり、操作変数の強さは推定値の精度に直接影響を与えます。相関が弱い場合、バイアスのある一貫性のない推定値をもたらす「弱い操作変数問題」が発生する可能性があります。

• 操作変数は回帰モデルにおいて誤差項と相関していない必要があります。これを外生性の条件とも呼びます。言い換えると、操作変数は内生的な説明変数以外の被説明変数に直接的な影響を与えていない必要があります。

これらの条件は直感的には簡単に思えるかもしれませんが、実践的には非常に検証が難しいことがあります。第一の条件は、提案された操作変数と内生変数との間の相関を確認することで経験的に検証することができます。しかし、第二の条件は一般的には検証不可能であり、観測されない変数を含むため、しばしば説得力のある主張や対象となるシステムの基本的なプロセスの理解に依存します。

因果推論における操作変数

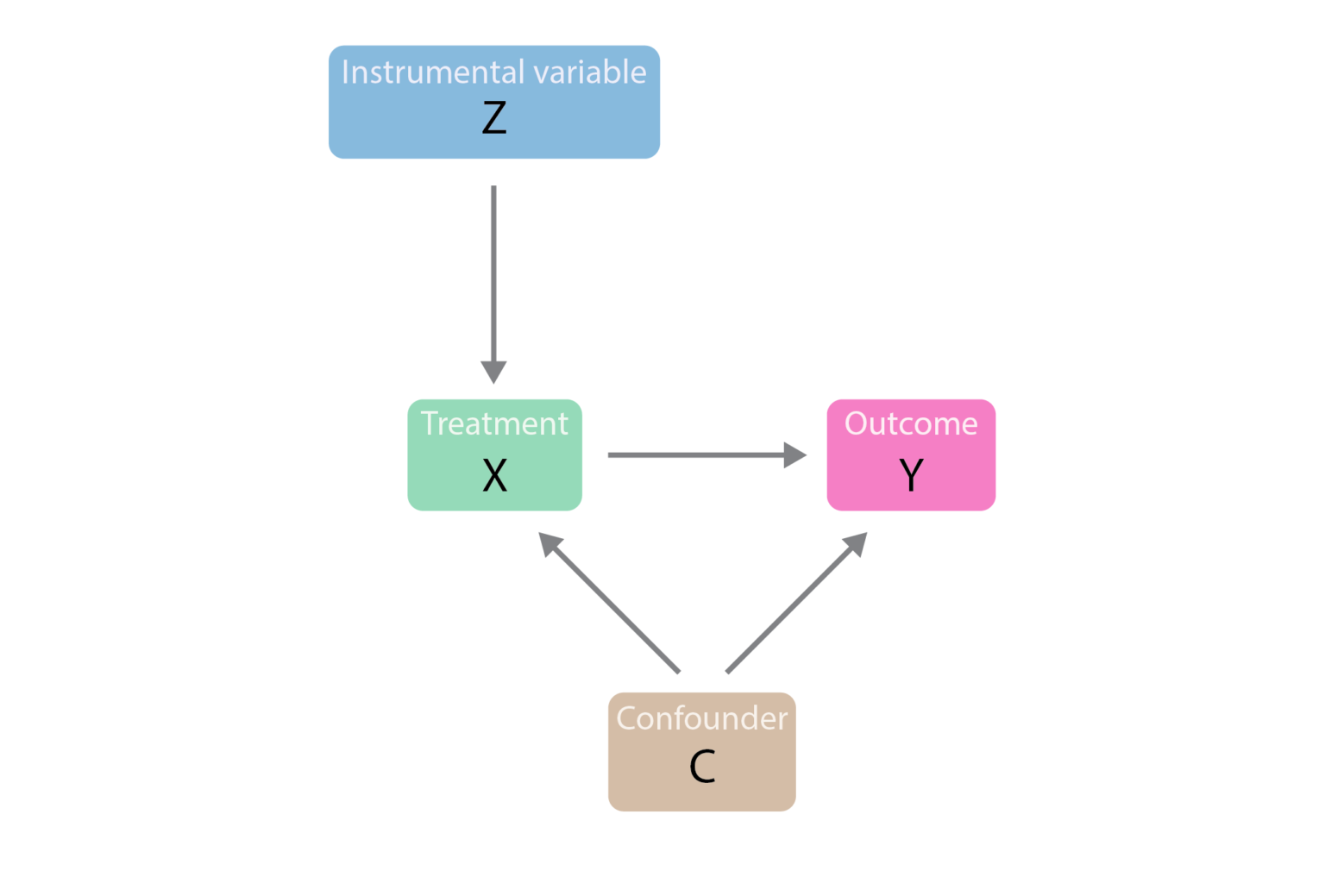
操作変数のアプローチは、主に観測データから未観測で直接制御不可能な交絡変数を考慮するため、因果推論のためのツールとして利用されます。操作変数は、説明変数と未観測の交絡要因や誤差項と相関しないが、説明変数と被説明変数との間の因果効果を分離するために使用されます。

3 Real-World Examples of Using Instrumental Variables

操作変数の導出

操作変数の導出は、内生性の存在する状況で因果効果を推定するための一般的な統計手法である2SLS（2ステージ最小二乗）回帰に依存しています。そのアイデアは、まず操作変数を使って内生的な説明変数を予測し、それからこれらの予測値を使用して因果効果を推定することです。

まず、次の単純な線形回帰モデルを考えます。

y = \beta_0 + \beta_1 x + u

このモデルでは、yは被説明変数、xは説明変数、\beta_0と\beta_1は興味のあるパラメータ、uは誤差項です。xが省略された変数、同時性、または測定誤差によってuと相関していると仮定します。これにより、\beta_1の推定値にバイアスが生じ、因果効果の推定に影響がおよびます。

zがxの操作変数であり、関連性の条件（zとxが相関している）および外生性の条件（zがuと相関していない）を満たすと仮定します。操作変数アプローチは次の2つのステップで行われます。

1. xをz（および他の外生変数）に回帰し、xの予測値\hat{x}を得ます。

\hat{x} = \pi_0 + \pi_1 z + v

ここで、\pi_0と\pi_1は推定されるパラメータであり、vは誤差項です。

2. yを\hat{x}（および他の外生変数）に回帰し、\beta_0と\beta_1の操作変数推定値を得ます。

y = \beta_0 + \beta_1 \hat{x} + \hat{u}

ここで、\hat{\beta_0}と\hat{\beta_1}は興味のあるパラメータであり、\hat{u}は誤差項です。

これらのステップにより、uと相関しない\hat{x}によってxの誤差項との相関を「クリーニング」し、因果効果の推定値\hat{\beta_1}を得ることができます。ただし、zが妥当な操作変数である場合に限り、これは\hat{\beta_1}のバイアスのない一貫性のある推定値となります。

なお、操作変数の推定値は、因果効果を受ける「適合者（compliers）」と呼ばれるサブポピュレーションにおける説明変数の効果である局所的な平均処置効果（LATE）のみを特定します。これは、説明変数の全集団に対する平均処置効果（ATE）とは異なる効果です。

参考

https://quantifyinghealth.com/examples-of-instrumental-variables/
https://www.statology.org/instrumental-variables/