Apa itu Regresi

Analisis regresi adalah teknik statistik yang digunakan untuk menyelidiki hubungan antara variabel-variabel. Ini memungkinkan kita memahami bagaimana nilai satu variabel, yang dikenal sebagai variabel dependen, berubah terhadap nilai satu atau lebih variabel independen. Analisis regresi sangat berguna untuk memprediksi perilaku variabel dependen dan mengidentifikasi hubungan kausal potensial antara variabel-variabel. Ini secara luas digunakan di berbagai bidang, termasuk keuangan, ekonomi, ilmu sosial, dan teknik.

Peran analisis regresi dalam statistik cukup signifikan, antara lain:

• Pemodelan prediktif
  Analisis regresi memungkinkan kita membuat model yang dapat digunakan untuk memprediksi variabel dependen berdasarkan nilai variabel independen. Hal ini sangat berharga untuk meramalkan tren masa depan atau membuat keputusan berdasarkan data.

• Menilai hubungan antar variabel
  Dengan memperkirakan hubungan antara variabel, analisis regresi memberikan wawasan tentang sifat dan kekuatan asosiasi. Informasi ini dapat berguna untuk pengujian hipotesis dan memahami potensi kausalitas.

• Mengidentifikasi faktor yang berpengaruh
  Analisis regresi membantu mengidentifikasi variabel independen yang memiliki dampak paling signifikan terhadap variabel dependen. Pengetahuan ini penting untuk mengembangkan intervensi atau strategi yang efektif.

Mean Kondisional

Mean kondisional merujuk pada nilai harapan variabel dependen yang diberikan nilai variabel independen. Dalam analisis regresi, mean kondisional direpresentasikan oleh model regresi, yang memperkirakan hubungan antara variabel dependen dan independen. Mean kondisional digunakan untuk membuat prediksi tentang variabel dependen berdasarkan variabel independen.

Sebagai contoh, dalam model regresi linier sederhana, mean kondisional dapat direpresentasikan sebagai:

di mana E(Y|X) menyatakan nilai harapan variabel dependen Y yang diberikan nilai variabel independen X, dan \beta_0 dan \beta_1 adalah parameter model regresi.

Distribusi Kondisional

Distribusi kondisional merujuk pada distribusi variabel dependen yang diberikan nilai variabel independen. Distribusi kondisional memberikan informasi tentang variasi variabel dependen sekitar mean kondisional. Ini membantu kita memahami dispersi dan bentuk variabel dependen untuk setiap nilai variabel independen.

Dalam analisis regresi, distribusi kondisional sering diasumsikan mengikuti keluarga distribusi probabilitas tertentu. Sebagai contoh, dalam regresi linier, diasumsikan bahwa distribusi kondisional variabel dependen adalah distribusi normal dengan mean sama dengan mean kondisional dan variansi konstan (homoskedastis).

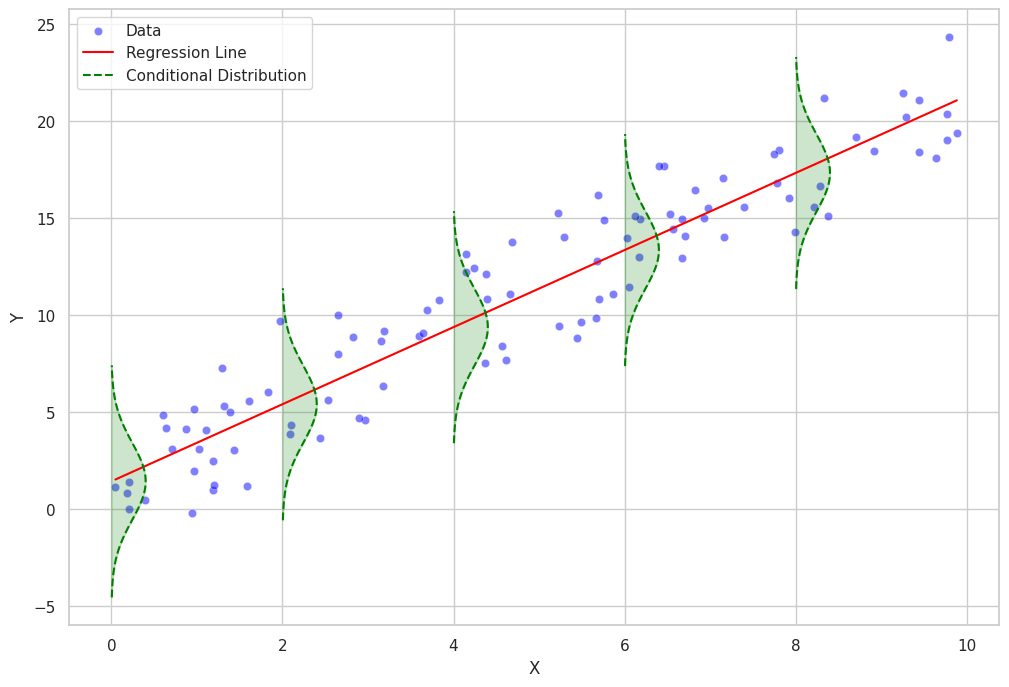
Pada model regresi yang lebih kompleks, seperti model regresi linear umum atau model regresi nonparametrik, distribusi kondisional dapat mengikuti keluarga distribusi probabilitas yang berbeda, seperti distribusi Poisson, binomial, atau gamma.

Metode Kuadrat Terkecil

Metode kuadrat terkecil adalah pendekatan yang banyak digunakan dalam analisis regresi untuk memperkirakan parameter model regresi. Pendekatan ini bekerja dengan meminimalkan jumlah kuadrat selisih antara nilai observasi variabel dependen dan nilai yang diprediksi oleh model. Metode ini memastikan garis terbaik (dalam kasus regresi linier) atau kurva terbaik (dalam kasus regresi nonlinear) diperoleh, yang secara akurat merepresentasikan hubungan antar variabel.

Formulasi Matematis Metode Kuadrat Terkecil

Metode kuadrat terkecil melibatkan meminimalkan jumlah kuadrat residual, di mana residual untuk setiap observasi adalah selisih antara nilai observasi variabel dependen dan nilai yang diprediksi oleh model.

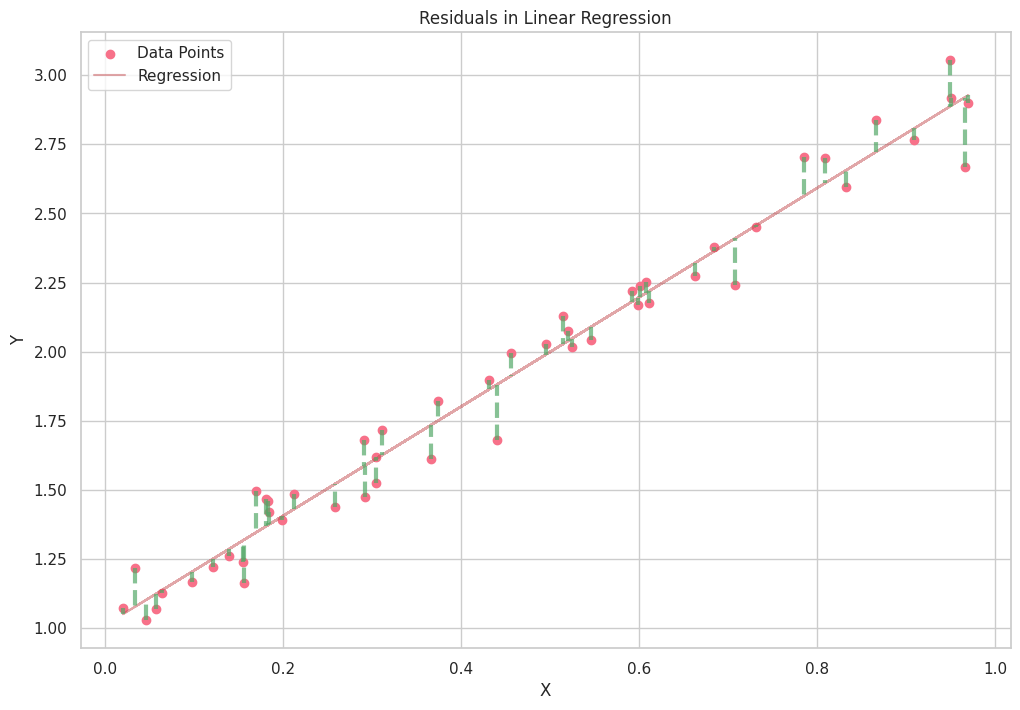
Dalam kasus regresi linier sederhana, model regresi dapat direpresentasikan sebagai:

di mana Y_i adalah nilai observasi variabel dependen untuk observasi ke-i, X_i adalah nilai variabel independen untuk observasi ke-i, \beta_0 dan \beta_1 adalah parameter yang akan diestimasi (intersep dan kemiringan, masing-masing), dan \epsilon_i adalah residual untuk observasi ke-i.

Tujuan dari metode kuadrat terkecil adalah untuk menemukan nilai \beta_0 dan \beta_1 yang meminimalkan jumlah kuadrat residual, yang diberikan oleh:

Untuk meminimalkan S(\beta_0, \beta_1), kita dapat mengambil turunan parsial terhadap \beta_0 dan \beta_1 dan menetapkannya sama dengan nol:

Mencari solusi simultan dari persamaan ini memberikan estimasi untuk \beta_0 dan \beta_1:

di mana \bar{X} dan \bar{Y} adalah nilai rata-rata variabel independen dan dependen, masing-masing.

Implementasi Analisis Regresi

Pada bab ini, saya akan menunjukkan bagaimana cara melakukan analisis regresi menggunakan Python.

Pertama, mari impor perpustakaan yang diperlukan:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression

Sekarang, mari buat beberapa data contoh untuk analisis regresi linear kita:

# Set a random seed for reproducibility
np.random.seed(42)

# Create the sample data
x = np.random.rand(50)
y = 2 * x + 1 + np.random.normal(0, 0.1, size=50)

# Store the data in a pandas DataFrame
data = pd.DataFrame({'X': x, 'Y': y})

Selanjutnya, mari cocokkan model regresi linear ke data kita:

# Fit a linear regression model
model = LinearRegression()
model.fit(data[['X']], data['Y'])

# Calculate the predicted values
data['Y_pred'] = model.predict(data[['X']])

Sekarang, mari buat plot titik data dan garis regresi:

# Set the style and color palette for the plot
sns.set_style("whitegrid")
sns.set_palette("husl")

# Create a scatter plot of the data points
plt.scatter(data['X'], data['Y'], label='Data Points')

# Plot the regression line
plt.plot(data['X'], data['Y_pred'], color='r', label='Regression Line')

# Add labels and a legend
plt.xlabel("X")
plt.ylabel("Y")
plt.legend(loc='best')
plt.title("Data Points and Regression Line")

# Show the plot
plt.show()

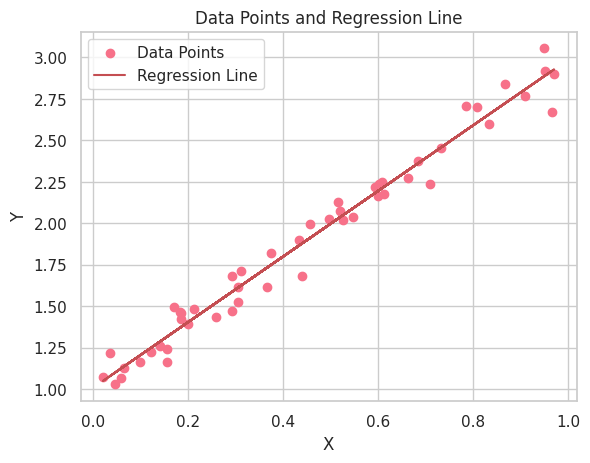
Sekarang bahwa kita telah memvisualisasikan data dan garis regresi, mari interpretasikan hasil dari analisis regresi linear kita. Hal pertama yang perlu diperhatikan adalah hubungan positif antara variabel X dan Y, karena garis regresi memiliki kemiringan positif. Hal ini menunjukkan bahwa ketika variabel X meningkat, variabel Y juga meningkat.

Selain memvisualisasikan data dan garis regresi, penting untuk menginterpretasikan parameter yang diestimasi (koefisien) dari model regresi linear. Persamaan regresi linear dapat ditulis sebagai berikut:

Di sini, Y mewakili variabel dependen, X mewakili variabel independen, \beta_0 dan \beta_1 adalah koefisien yang diestimasi, dan \epsilon mewakili residu (istilah kesalahan).

\beta_0 (intersep) mewakili nilai yang diestimasi dari Y ketika X sama dengan 0, sedangkan \beta_1 (kemiringan) mewakili perubahan yang diestimasi pada Y untuk peningkatan satu unit pada X.

Mari ambil parameter yang diestimasi dari model regresi linear kita dan interpretasikan:

# Get the estimated parameters
intercept, slope = model.intercept_, model.coef_[0]

print(f"Intercept (β0): {intercept:.3f}")
print(f"Slope (β1): {slope:.3f}")

Intercept (β0): 1.010
Slope (β1): 1.978

Dalam contoh ini, intersep yang diestimasi \beta_0 adalah sekitar 1, dan kemiringan yang diestimasi \beta_1 adalah sekitar 2. Ini berarti bahwa ketika X sama dengan 0, nilai yang diprediksi dari Y adalah sekitar 1. Selain itu, untuk setiap peningkatan satu unit pada X, nilai yang diprediksi dari Y meningkat sekitar 2 unit.

Perlu diingat bahwa hubungan sebenarnya antara X dan Y pada data contoh kita adalah Y = 1 + 2X + noise. Koefisien yang diestimasi cukup dekat dengan koefisien sebenarnya, yang menunjukkan bahwa model regresi linear kita telah berhasil menangkap hubungan mendasar antara variabel. Namun, pada skenario dunia nyata, hubungan sebenarnya antara variabel seringkali tidak diketahui, dan tujuan dari analisis regresi adalah untuk mengungkap hubungan ini dan membuat prediksi berdasarkan parameter yang diestimasi.

Skrip Python untuk Plotting Distribusi Kondisional dan Residual

Berikut ini adalah skrip Python untuk memplot distribusi kondisional dan residual.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from scipy.stats import norm

# Set seaborn style
sns.set(style="whitegrid")

# Generate a dataset
np.random.seed(0)
n = 100
x = np.random.uniform(0, 10, n)
y = 2 * x + 1 + np.random.normal(0, 2, n)
data = pd.DataFrame({"x": x, "y": y})

# Fit a linear regression model
model = LinearRegression()
model.fit(data[["x"]], data["y"])


# Add regression line to the dataset
data["y_pred"] = model.predict(data[["x"]])

rmse = np.sqrt(mean_squared_error(data["y"], data["y_pred"]))

def plot_conditional_distributions_filled(data, intervals, model):
    fig, ax = plt.subplots(figsize=(12, 8))

    # Scatter plot of the data points
    sns.scatterplot(data=data, x="x", y="y", color="blue", alpha=0.5, label="Data", ax=ax)

    # Regression line
    sns.lineplot(data=data, x="x", y="y_pred", color="red", label="Regression Line", ax=ax)


    for i in range(len(intervals) - 1):
        lower = intervals[i]
        upper = intervals[i + 1]
        mask = (data["x"] >= lower) & (data["x"] < upper)

        if mask.sum() > 0:
            subset = data[mask]
            mean = model.intercept_ + model.coef_[0] * lower
            std = rmse

            # Plot Gaussian curve
            x_vals = np.linspace(mean - 3 * std, mean + 3 * std, 100)
            y_vals = norm.pdf(x_vals, mean, std)
            y_vals = y_vals * (upper - lower) + lower

            ax.plot(y_vals, x_vals, color="green", linestyle="--", label="Conditional Distribution" if i == 0 else None)

            # Fill the Gaussian curve
            ax.fill_betweenx(x_vals, lower, y_vals, color="green", alpha=0.2)

    ax.set_xlabel("X")
    ax.set_ylabel("Y")
    ax.legend()
    plt.show()

# Define intervals for Gaussian curves
intervals = np.arange(0, 12, 2)

# Plot the conditional distributions with filled Gaussian curves
plot_conditional_distributions_filled(data, intervals, model)

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression

# Set a random seed for reproducibility
np.random.seed(42)

# Create the sample data
x = np.random.rand(50)
y = 2 * x + 1 + np.random.normal(0, 0.1, size=50)

# Store the data in a pandas DataFrame
data = pd.DataFrame({'X': x, 'Y': y})

# Fit a linear regression model
model = LinearRegression()
model.fit(data[['X']], data['Y'])

# Calculate the predicted values
data['Y_pred'] = model.predict(data[['X']])

# Set the style and color palette for the plot
sns.set_style("whitegrid")
sns.set_palette("husl")

plt.subplots(figsize=(12, 8))

# Create a scatter plot of the data points
plt.scatter(data['X'], data['Y'], label='Data Points')

# Plot the regression line
plt.plot(data['X'], data['Y_pred'], color='r', label='Regression', alpha=0.5)

# Calculate and plot the residuals
for _, row in data.iterrows():
    plt.plot([row['X'], row['X']], [row['Y'], row['Y_pred']], color='g', linewidth=3, linestyle='--', alpha=0.7)

# Add labels and a legend
plt.xlabel("X")
plt.ylabel("Y")
plt.legend(loc='best')
plt.title("Residuals in Linear Regression")

# Show the plot
plt.show()