2022-11-20

Regresi Linier

Machine Learning

Regression

Python

sklearn

Apa itu Linear Regression

Regresi linier adalah algoritma pembelajaran mesin yang digunakan untuk memodelkan hubungan antara variabel dependen (juga dikenal sebagai variabel respons, hasil, dan tujuan) dan satu atau lebih variabel independen (juga dikenal sebagai prediktor, fitur, atau variabel input). Tujuan utama dari regresi linier adalah untuk memprediksi nilai variabel dependen berdasarkan nilai variabel independen. Hal ini dicapai dengan memasangkan persamaan linier pada titik data yang diamati, yang dapat direpresentasikan sebagai garis lurus dalam kasus regresi linier sederhana atau sebagai hiperbidang untuk regresi linier berganda.

Prinsip dasar dari regresi linier adalah meminimalkan perbedaan antara nilai prediksi dan nilai aktual. Perbedaan ini, yang dikenal sebagai residual, adalah jarak vertikal antara titik data dan garis atau hiperbidang yang cocok. Dengan meminimalkan jumlah kuadrat residual, kita mendapatkan garis atau hiperbidang yang cocok terbaik yang dapat digunakan untuk membuat prediksi tentang variabel dependen.

Asumsi dalam Regresi Linier

Untuk memastikan bahwa model regresi linier memberikan prediksi yang akurat dan dapat diandalkan, beberapa asumsi harus dipenuhi:

Linearitas
Harus ada hubungan linear antara variabel dependen dan independen. Hal ini dapat diperiksa menggunakan plot pencar atau koefisien korelasi.
Independensi
Variabel independen tidak boleh saling berkorelasi tinggi. Multikolinieritas dapat menyebabkan estimasi yang tidak stabil dan dapat diatasi dengan menghapus variabel yang redundan atau menggunakan teknik regularisasi.
Homoskedastisitas
Varians dari residual harus konstan di semua tingkat variabel independen. Heteroskedastisitas dapat dideteksi menggunakan plot pencar atau tes diagnostik dan dapat diatasi dengan menggunakan kuadrat terkecil terbobot atau mentransformasi variabel dependen.
Normalitas
Residual harus terdistribusi normal. Hal ini dapat diperiksa menggunakan histogram, Q-Q plot, atau tes statistik seperti tes Shapiro-Wilk. Non-normalitas dapat diatasi dengan mentransformasi variabel dependen atau menggunakan teknik regresi yang kokoh.
Independensi Kesalahan
Residual harus saling independen. Hal ini dapat diperiksa menggunakan tes Durbin-Watson atau dengan memplot residual terhadap waktu atau nilai prediksi. Autokorelasi dapat diatasi dengan menggunakan model deret waktu atau menggabungkan variabel lag.

Regresi Linier Sederhana

Pada regresi linier sederhana, tujuannya adalah untuk menetapkan hubungan linear antara satu variabel independen ( $X$ ) dan variabel dependen ( $Y$ ). Persamaan untuk hubungan ini dapat ditulis sebagai:

$Y = \beta_0 + \beta_1X + \epsilon$

dimana:

$Y$ adalah variabel dependen
$X$ adalah variabel independen
$\beta_0$ adalah intercept garis (nilai $Y$ ketika $X$ sama dengan 0)
$\beta_1$ adalah kemiringan garis (perubahan $Y$ untuk perubahan satuan pada $X$ )
$\epsilon$ adalah istilah kesalahan (perbedaan antara nilai aktual dan prediksi $Y$ )

Garis yang cocok terbaik adalah garis yang meminimalkan jumlah kuadrat residual (perbedaan kuadrat antara nilai aktual dan prediksi $Y$ ).

Metode Kuadrat Terkecil

Metode kuadrat terkecil adalah pendekatan matematis untuk menemukan garis yang cocok terbaik dengan meminimalkan jumlah kuadrat residual. Estimasi untuk intercept dan kemiringan garis terbaik dapat dihitung menggunakan formula berikut:

$\beta_1 = \frac{\sum_{i=1}^n (X_i - \bar{X})(Y_i - \bar{Y})}{\sum_{i=1}^n (X_i - \bar{X})^2}$

$\beta_0 = \bar{Y} - \beta_1\bar{X}$

dimana:

$n$ adalah jumlah titik data
$X_i$ dan $Y_i$ adalah titik data individu
$\bar{X}$ dan $\bar{Y}$ adalah rata-rata variabel independen dan dependen, secara berturut-turut

Evaluasi Kinerja Model

Setelah garis yang cocok terbaik diperoleh, kita perlu mengevaluasi kinerja model untuk memastikan bahwa itu adalah fit yang baik untuk data. Beberapa metrik umum yang digunakan untuk mengevaluasi kinerja model regresi linier sederhana adalah:

Koefisien Determinasi (R^2)

Metrik ini mengukur proporsi variansi pada variabel dependen yang dapat dijelaskan oleh variabel independen. Nilai $R^2$ yang mendekati 1 menunjukkan hubungan yang kuat, sedangkan nilai $R^2$ yang mendekati 0 menunjukkan hubungan yang lemah.

$R^2 = 1 - \frac{\sum_{i=1}^n (Y_i - \hat{Y}i)^2}{\sum{i=1}^n (Y_i - \bar{Y})^2}$

dimana:

$\hat{Y}_i$ adalah nilai prediksi $Y$ untuk titik data ke- $i$

Mean Squared Error (MSE)

Metrik ini menghitung rata-rata perbedaan kuadrat antara nilai aktual dan prediksi variabel dependen.

$MSE = \frac{1}{n}\sum_{i=1}^n (Y_i - \hat{Y}_i)^2$

MSE yang lebih rendah menunjukkan model yang lebih baik sesuai dengan data.

Regresi Linier Berganda

Regresi linier berganda memperluas konsep regresi linier sederhana untuk mencakup beberapa variabel independen. Persamaan untuk hubungan antara variabel dependen ( $Y$ ) dan variabel independen ( $X_1, X_2, ..., X_p$ ) dapat ditulis sebagai:

$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_pX_p + \epsilon$

dimana:

$Y$ adalah variabel dependen
$X_1, X_2, ..., X_p$ adalah variabel independen
$\beta_0$ adalah intercept dari hiperruang
$\beta_1, \beta_2, ..., \beta_p$ adalah koefisien untuk variabel independen
$\epsilon$ adalah istilah kesalahan (perbedaan antara nilai aktual dan prediksi $Y$ )

Pendekatan Matrix

Pada regresi linier berganda, kita menggunakan pendekatan matriks untuk memperkirakan koefisien variabel independen. Estimasi kuadrat terkecil dapat diperoleh dengan menyelesaikan persamaan matriks berikut:

$\boldsymbol{\beta} = (\mathbf{X}^T\mathbf{X})^{-1}\mathbf{X}^T\mathbf{Y}$

dimana:

$\boldsymbol{\beta}$ adalah vektor yang berisi koefisien ( $\beta_0, \beta_1, ..., \beta_p$ )
$\mathbf{X}$ adalah matriks variabel independen, dengan setiap baris mewakili titik data dan setiap kolom mewakili variabel independen
$\mathbf{Y}$ adalah vektor nilai variabel dependen

Menangani Multikolinearitas

Multikolinearitas muncul ketika dua atau lebih variabel independen sangat berkorelasi. Hal ini dapat menyebabkan perkiraan yang tidak stabil dan membuat sulit untuk menginterpretasikan koefisien variabel independen. Untuk mendeteksi multikolinearitas, kita dapat menghitung faktor inflasi varian (VIF) untuk setiap variabel independen:

$VIF_i = \frac{1}{1 - R_i^2}$

dimana $R_i^2$ adalah nilai $R^2$ yang diperoleh dengan meregresi variabel independen ke- $i$ pada variabel independen lainnya. Nilai VIF yang lebih besar dari 10 menunjukkan tingkat multikolinearitas yang tinggi.

Untuk mengatasi multikolinearitas, kita dapat:

Menghapus salah satu variabel yang berkorelasi
Menggabungkan variabel yang berkorelasi menjadi satu variabel (misalnya, dengan mengambil rata-rata mereka)
Menggunakan teknik regularisasi seperti ridge atau lasso regression

Seleksi Fitur dan Skala

Dalam regresi linier berganda, penting untuk memilih variabel independen yang paling relevan untuk menghindari overfitting dan meningkatkan interpretabilitas model. Teknik seleksi fitur, seperti regresi bertahap, eliminasi fitur rekursif, dan LASSO, dapat digunakan untuk mengidentifikasi variabel yang paling penting.

Selain itu, ketika variabel independen memiliki skala yang berbeda, sulit untuk membandingkan koefisien mereka. Dalam hal ini, metode pengukuran fitur, seperti normalisasi atau standardisasi, dapat diterapkan untuk membawa semua variabel ke skala yang serupa.

Mengimplementasikan Regresi Linier di Python

Pada bab ini, saya akan mengimplementasikan regresi linier sederhana dan berganda menggunakan Python dan dataset Perumahan California. Dataset ini adalah pilihan populer untuk tugas regresi dan tersedia di perpustakaan scikit-learn.

Pertama, mari impor perpustakaan yang diperlukan dan muat dataset Perumahan California dari perpustakaan scikit-learn.

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# Load the California Housing dataset
dataset = fetch_california_housing()
X = pd.DataFrame(dataset.data, columns=dataset.feature_names)
y = dataset.target

# Display the first few rows of the dataset
print(X.head())

	MedInc	HouseAge	AveRooms	AveBedrms	Population	AveOccup	Latitude	Longitude
0	8.3252	41.0	6.984127	1.023810	322.0	2.555556	37.88	-122.23
1	8.3014	21.0	6.238137	0.971880	2401.0	2.109842	37.86	-122.22
2	7.2574	52.0	8.288136	1.073446	496.0	2.802260	37.85	-122.24
3	5.6431	52.0	5.817352	1.073059	558.0	2.547945	37.85	-122.25
4	3.8462	52.0	6.281853	1.081081	565.0	2.181467	37.85	-122.25

Regresi Linier Sederhana

Kita akan memulai dengan mengimplementasikan regresi linier sederhana menggunakan fitur MedInc, yang mewakili pendapatan median di area tertentu, untuk memprediksi harga rumah median.

Pisahkan data menjadi set pelatihan dan pengujian.

python

X_simple = X[["MedInc"]]
X_train_simple, X_test_simple, y_train, y_test = train_test_split(X_simple, y, test_size=0.2, random_state=42)

Buat model regresi linier sederhana dan sesuaikan dengan data pelatihan.

python

simple_lr = LinearRegression()
simple_lr.fit(X_train_simple, y_train)

Evaluasi kinerja model menggunakan MSE dan skor $R^2$ .

python

y_pred_simple = simple_lr.predict(X_test_simple)
mse_simple = mean_squared_error(y_test, y_pred_simple)
r2_simple = r2_score(y_test, y_pred_simple)

print("Simple Linear Regression - MSE:", mse_simple)
print("Simple Linear Regression - R² Score:", r2_simple)

Simple Linear Regression - MSE: 0.7091157771765549
Simple Linear Regression - R² Score: 0.45885918903846656

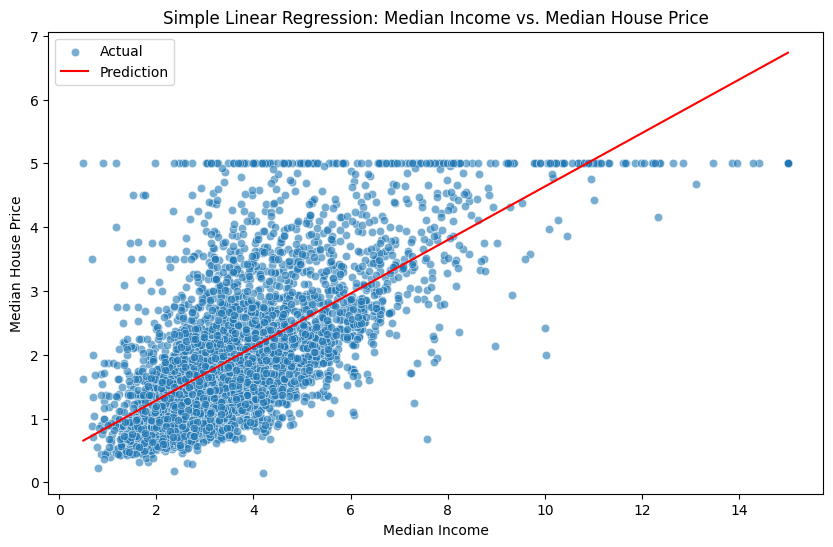
Plot garis terbaik menggunakan matplotlib dan seaborn.

python

plt.figure(figsize=(10, 6))
sns.scatterplot(x=X_test_simple["MedInc"], y=y_test, alpha=0.6, label="Actual")
sns.lineplot(x=X_test_simple["MedInc"], y=y_pred_simple, color="red", label="Prediction")
plt.xlabel("Median Income")
plt.ylabel("Median House Price")
plt.title("Simple Linear Regression: Median Income vs. Median House Price")
plt.legend()
plt.show()

Simple linear regression

Regresi Linier Berganda

Sekarang mari kita implementasikan regresi linier berganda menggunakan semua fitur dalam dataset.

Pisahkan data menjadi set pelatihan dan pengujian.

python

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Buat model regresi linier berganda dan sesuaikan dengan data pelatihan.

multiple_lr = LinearRegression()
multiple_lr.fit(X_train, y_train)

Evaluasi kinerja model menggunakan mean squared error (MSE) dan skor $R^2$ .

python

y_pred_multiple = multiple_lr.predict(X_test)
mse_multiple = mean_squared_error(y_test, y_pred_multiple)
r2_multiple = r2_score(y_test, y_pred_multiple)

print("Multiple Linear Regression - MSE:", mse_multiple)
print("Multiple Linear Regression - R² Score:", r2_multiple)

Multiple Linear Regression - MSE: 0.5558915986952444
Multiple Linear Regression - R² Score: 0.5757877060324508

Sekarang mari kita bandingkan kinerja model regresi linier sederhana dan berganda menggunakan MSE dan skor $R^2$ mereka.

python

print("Simple Linear Regression - MSE:", mse_simple)
print("Simple Linear Regression - R² Score:", r2_simple)
print("Multiple Linear Regression - MSE:", mse_multiple)
print("Multiple Linear Regression - R² Score:", r2_multiple)

Simple Linear Regression - MSE: 0.709
Simple Linear Regression - R² Score: 0.459
Multiple Linear Regression - MSE: 0.556
Multiple Linear Regression - R² Score: 0.576

Berdasarkan hasilnya, model regresi linier berganda pada umumnya harus memiliki MSE yang lebih rendah dan skor $R^2$ yang lebih tinggi dibandingkan dengan model regresi linier sederhana. Hal ini menunjukkan bahwa model regresi linier berganda lebih cocok untuk data dan dapat lebih baik memprediksi harga rumah median menggunakan fitur yang diberikan.