Apa itu Statistik inferensial

Statistik inferensial adalah cabang statistika yang memungkinkan para peneliti untuk membuat kesimpulan tentang populasi berdasarkan informasi yang dikumpulkan dari sampel. Ini melibatkan membuat generalisasi, prediksi, dan estimasi tentang populasi dengan menganalisis karakteristik dan pola yang diamati pada sampel. Statistik inferensial memainkan peran penting dalam berbagai bidang, termasuk ilmu sosial, ilmu alam, ekonomi, dan kedokteran.

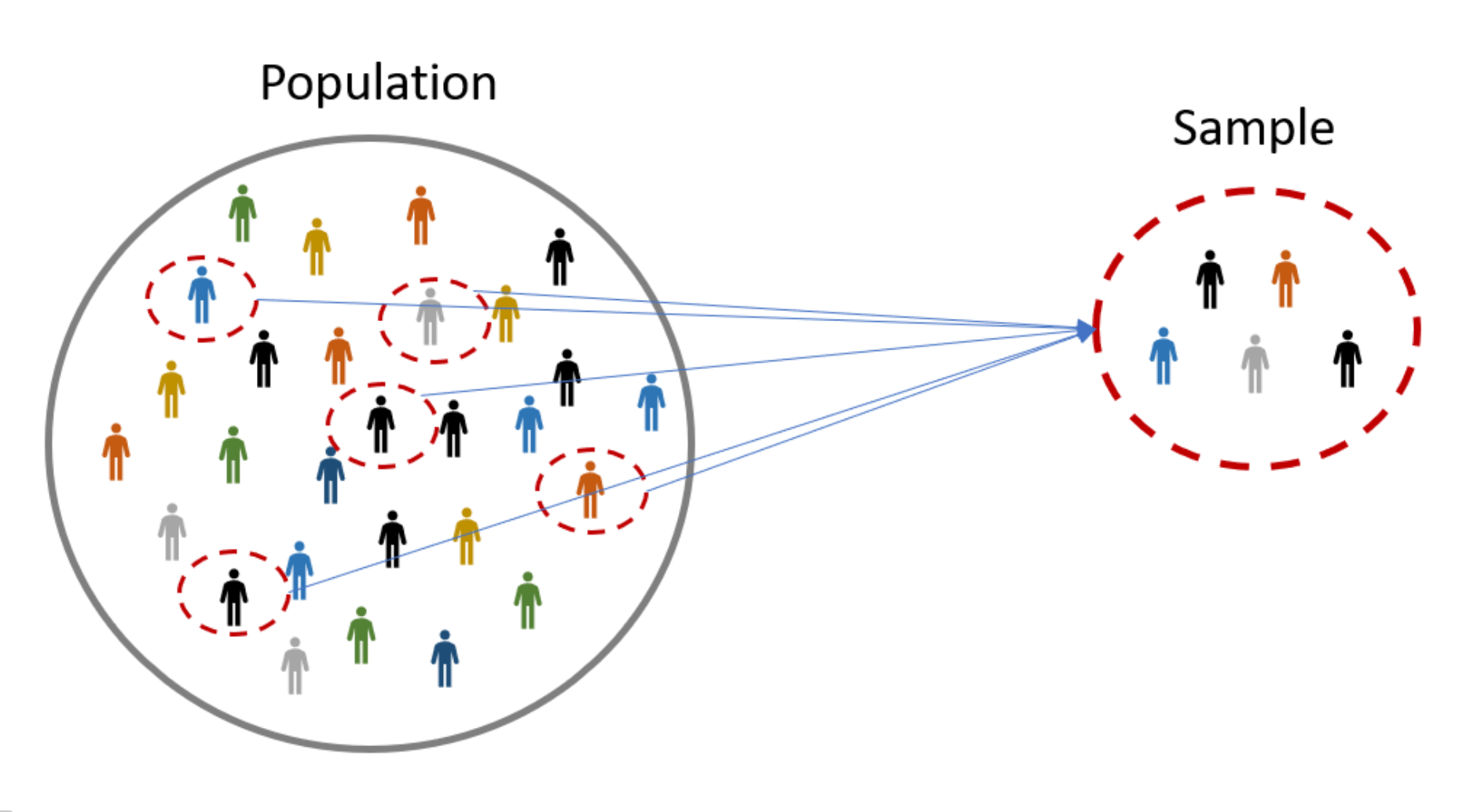
Populasi dan Sampel

Populasi mengacu pada himpunan lengkap individu, objek, atau pengamatan yang menarik minat para peneliti. Dalam kebanyakan kasus, studi terhadap seluruh populasi tidak mungkin dilakukan karena keterbatasan waktu, biaya, dan logistik. Oleh karena itu, para peneliti mengandalkan sampel, yang merupakan subset dari populasi, untuk mengumpulkan informasi dan membuat inferensi tentang populasi.

Sample size definition

Estimasi dan Uji Statistik

Statistik inferensial memiliki dua jenis utama: estimasi dan uji hipotesis.

Estimasi

Estimasi adalah konsep fundamental dalam statistik inferensial yang melibatkan penggunaan data sampel untuk memperkirakan parameter populasi. Ada dua jenis teknik estimasi utama: estimasi titik dan estimasi interval. Secara umum, teknik estimasi bertujuan untuk memberikan perkiraan yang akurat dan tepat dari parameter populasi, sambil mempertimbangkan ketidakpastian dan variasi yang terkait dengan proses pengambilan sampel.

Uji Hipotesis

Uji hipotesis adalah teknik inferensial yang banyak digunakan yang memungkinkan para peneliti untuk mengevaluasi bukti yang mendukung atau menentang klaim atau asumsi tertentu tentang parameter populasi. Proses pengujian hipotesis melibatkan langkah-langkah berikut:

1. Rumuskan hipotesis nol (H0) dan hipotesis alternatif (H1)
   Hipotesis nol adalah pernyataan bahwa tidak ada efek atau hubungan antara variabel yang menarik minat, sedangkan hipotesis alternatif menunjukkan adanya efek atau hubungan.

2. Pilih statistik uji yang sesuai
   Statistik uji adalah nilai numerik yang dihitung dari data sampel dan digunakan untuk mengevaluasi bukti terhadap hipotesis nol. Tes statistik yang berbeda memiliki statistik uji yang berbeda, tergantung pada jenis data dan asumsi yang dibuat tentang populasi.

3. Tentukan distribusi sampel dari statistik uji di bawah hipotesis nol
   Langkah ini melibatkan identifikasi distribusi statistik uji jika hipotesis nol benar. Distribusi sampel memungkinkan para peneliti untuk menghitung probabilitas mengamati statistik uji atau nilai yang lebih ekstrem, mengasumsikan hipotesis nol benar.

4. Hitung nilai p
   Nilai p adalah probabilitas mengamati statistik uji seekstrem atau lebih ekstrem dari yang dihitung dari data sampel, dengan asumsi hipotesis nol benar. Nilai p yang kecil (biasanya kurang dari 0,05) menunjukkan bukti yang kuat terhadap hipotesis nol, dan para peneliti dapat menolak hipotesis nol untuk mendukung hipotesis alternatif.

5. Buat keputusan
   Berdasarkan nilai p dan tingkat signifikansi yang telah ditentukan sebelumnya (biasanya 0,05), para peneliti memutuskan apakah akan menolak atau gagal menolak hipotesis nol. Jika nilai p kurang dari tingkat signifikansi, hasilnya dianggap signifikan secara statistik, dan hipotesis nol ditolak.

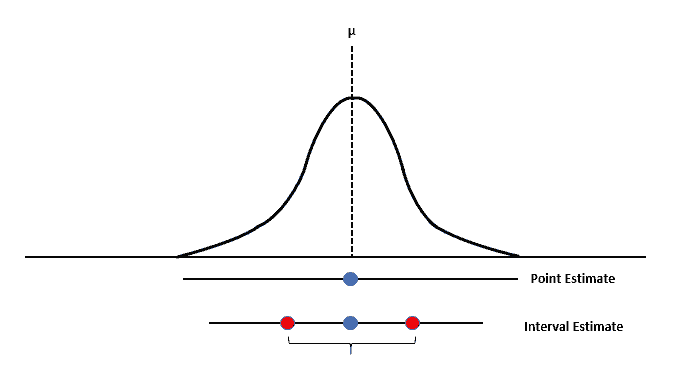
Estimasi Titik dan Estimasi Interval

Point and Interval Estimation

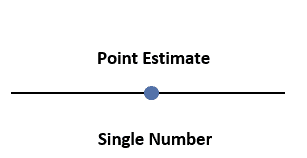
Estimasi Titik

Estimasi titik melibatkan menggunakan data sampel untuk menghitung nilai tunggal yang menjadi perkiraan terbaik dari parameter populasi. Estimator titik adalah statistik yang memberikan estimasi seperti itu, dan beberapa estimator titik yang umum meliputi rata-rata sampel (untuk memperkirakan rata-rata populasi) dan proporsi sampel (untuk memperkirakan proporsi populasi).

Point and Interval Estimation

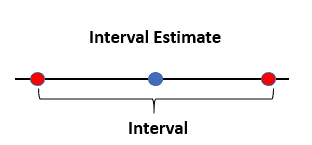
Estimasi Interval: Interval Kepercayaan

Sementara estimator titik memberikan nilai tunggal sebagai perkiraan terbaik dari parameter populasi, mereka tidak menyampaikan ketidakpastian yang terkait dengan proses estimasi. Estimasi interval mengatasi masalah ini dengan menyediakan rentang nilai di mana parameter populasi mungkin berada, bersama dengan tingkat kepercayaan yang ditentukan.

Point and Interval Estimation

Interval kepercayaan adalah jenis estimasi interval yang umum, dan mereka dibangun menggunakan estimator titik, standar error dari estimasi, dan nilai kritis dari distribusi probabilitas yang sesuai (seperti distribusi t atau distribusi normal). Interval kepercayaan biasanya dinyatakan dalam bentuk:

Estimator titik ± (Nilai kritis × Standar error)

Tingkat kepercayaan (biasanya 95%) mewakili probabilitas bahwa interval kepercayaan mengandung parameter populasi yang sebenarnya dalam pengambilan sampel yang berulang-ulang.