2022-12-23

Model linier umum

Apa itu model linier umum (GLM)?

Model linier umum (Generalized linier Model; GLM) adalah model statistik yang dapat diterapkan bahkan ketika variabel tujuan mengikuti distribusi probabilitas selain distribusi normal.

Analisis regresi sederhana atau berganda disebut model linier dan merupakan model statistik yang mengasumsikan bahwa variabel tujuan mengikuti distribusi normal. Jika variabel tujuan tidak dapat diasumsikan mengikuti distribusi normal, misalnya, jika variabel tujuan adalah variabel diskrit seperti data kategorikal atau hitungan, model linier tidak dapat diterapkan. GLM tidak hanya dapat menangani distribusi normal tetapi juga distribusi lain yang disebut keluarga distribusi eksponensial seperti distribusi binomial, gamma, dan Poisson.

Dalam GLM, hubungan antara variabel tujuan dan variabel penjelas tidak perlu berupa persamaan linier sederhana, tetapi dapat dinyatakan sebagai berikut:

g(y) = \beta_0x_0 + \beta_1x_1 + \cdots + \beta_nx_n

$\beta$ adalah parameter, $x$ adalah variabel penjelas, dan $n$ adalah jumlah variabel penjelas. Sisi kanan dari persamaan di atas digabungkan secara linier dan disebut prediktor linier. Dan, fungsi sisi kiri $g(y)$ disebut fungsi link.

Kombinasi distribusi probabilitas dan fungsi link

Kombinasi distribusi probabilitas dan fungsi link yang umum digunakan adalah seperti tabel di bawah ini.

	Distribusi probabilitas	Fungsi link
Diskrit	Distribusi binomial	logit
Diskrit	Distribusi Poisson	log
Diskrit	Distribusi binomial negatif	log
Berkelanjutan	Distribusi Gamma	log
Berkelanjutan	Distribusi normal	identity

Membangun GLM

Mari kita benar-benar membangun GLM. Mari kita pertimbangkan data jumlah benih dari 100 tanaman fiktif. Data terdiri dari kolom-kolom berikut:

y: Jumlah biji dari individu-individu
x: Ukuran individu
f: apakah individu-individu tersebut telah diberi pupuk atau tidak (C: tanpa pupuk, T: dengan pupuk)

import pandas as pd

# number of seeds
y = [6,6,6,12,10,4,9,9,9,11,6,10,6,10,11,8,3,8,5,5,4,11,5,10,6,6,7,9,3,10,2,9,10,
     5,11,10,4,8,9,12,8,9,8,6,6,10,10,9,12,6,14,6,7,9,6,7,9,13,9,13,7,8,10,7,12,
     6,15,3,4,6,10,8,8,7,5,6,8,9,9,6,7,10,6,11,11,11,5,6,4,5,6,5,8,5,9,8,6,8,7,9]

# body size
x = [8.31,9.44,9.5,9.07,10.16,8.32,10.61,10.06,9.93,10.43,10.36,10.15,10.92,8.85,
     9.42,11.11,8.02,11.93,8.55,7.19,9.83,10.79,8.89,10.09,11.63,10.21,9.45,10.44,
     9.44,10.48,9.43,10.32,10.33,8.5,9.41,8.96,9.67,10.26,10.36,11.8,10.94,10.25,
     8.74,10.46,9.37,9.74,8.95,8.74,11.32,9.25,10.14,9.05,9.89,8.76,12.04,9.91,
     9.84,11.87,10.16,9.34,10.17,10.99,9.19,10.67,10.96,10.55,9.69,10.91,9.6,
     12.37,10.54,11.3,12.4,10.18,9.53,10.24,11.76,9.52,10.4,9.96,10.3,11.54,9.42,
     11.28,9.73,10.78,10.21,10.51,10.73,8.85,11.2,9.86,11.54,10.03,11.88,9.15,8.52,
     10.24,10.86,9.97]

# feed (C: control, T: treatment)
f = ['C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
     'C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
     'C','C','C','C','C','C','C','C','C','C','C','C','T','T','T','T','T','T','T',
     'T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
     'T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
     'T','T','T','T','T']

df = pd.DataFrame(list(zip(y, x, f)), columns =['y', 'x', 'f'])

display(df.head())

	y	x	f
0	6	8.31	C
1	6	9.44	C
2	6	9.50	C
3	12	9.07	C
4	10	10.16	C

Investigasi data

Mari kita periksa statistik deskriptif.

df.describe()

	y	x
count	100.000000	100.000000
mean	7.830000	10.089100
std	2.624881	1.008049
min	2.000000	7.190000
25%	6.000000	9.427500
50%	8.000000	10.155000
75%	10.000000	10.685000
max	15.000000	12.400000

Menampilkan jumlah C dan T untuk f, masing-masing.

print('num of C:', len(df[df['f'] == 'C']))
print('num of T:', len(df[df['f'] == 'T']))

num of C: 50
num of T: 50

Statistik deskriptif dari data mengkonfirmasi hal-hal berikut ini:

Jumlah benih y:
- Bilangan bulat non-negatif (2 sampai 15).
- Rata-rata dan varians cukup dekat.
Ukuran individu x:
- Bilangan real positif (nilai kontinu)
- Variansnya kecil.
Perlakuan pemupukan f:
- Ini adalah variabel kategorikal.
- Jumlah elemen dalam setiap kategori adalah sama.

Selanjutnya, kita memvisualisasikan data. Pertama, scatter plot ditampilkan.

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))
sns.set(rc={'figure.figsize':(10,5)})

sns.scatterplot(x='x', y='y', hue='f', data=df)

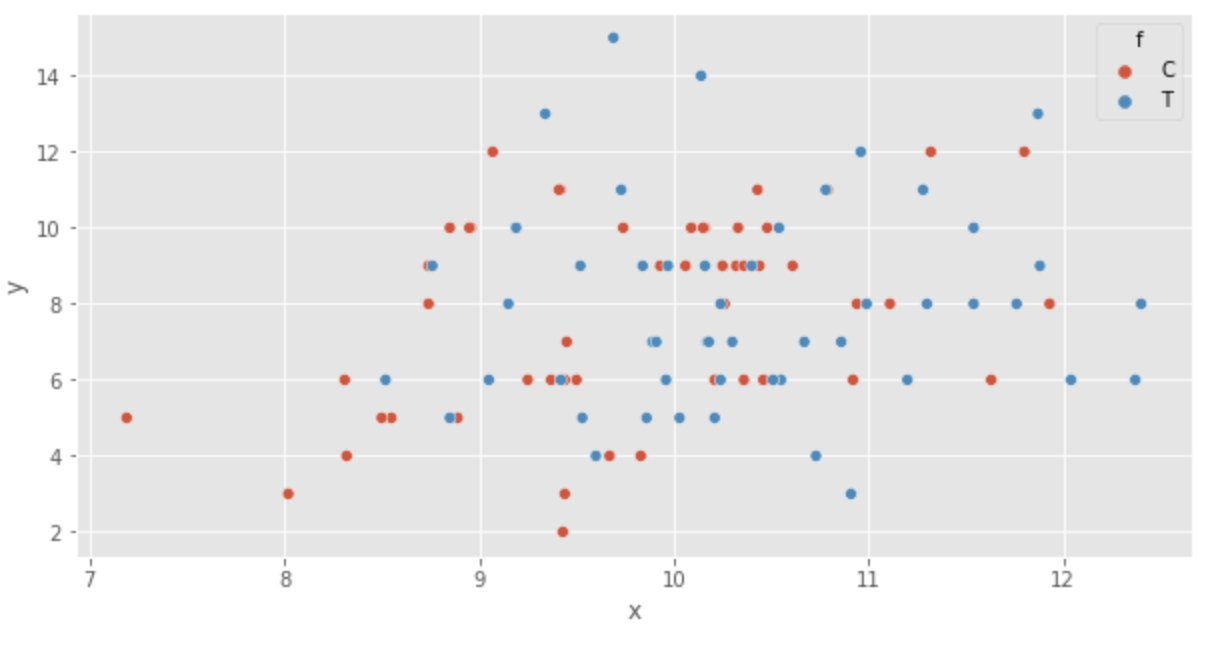
Scatter of f

Menampilkan diagram kotak-dan-whisker.

sns.boxplot(x='f', y='y', data=df)

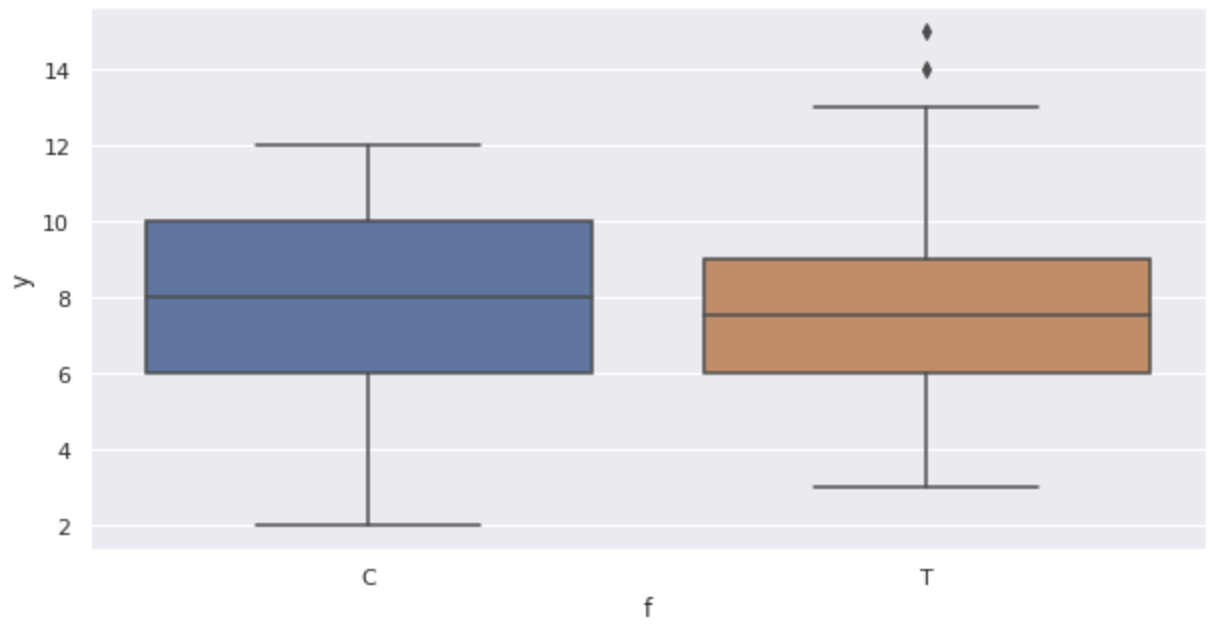
Box of f

Grafik menegaskan hal berikut ini:

Ketika ukuran $x$ meningkat, jumlah benih y juga meningkat (scatter plot)
Tampaknya tidak ada efek pupuk (diagram kotak-dan-whisker)

Membangun model statistik dengan regresi Poisson

Asumsikan bahwa jumlah biji $y_i$ dari beberapa individu tanaman fiktif $i$ mengikuti [distribusi Poisson] (/en/articles/poisson-distribution). Distribusi probabilitas dari distribusi Poisson adalah persamaan berikut

P(X=y| \lambda) = \frac{e^{-\lambda} \lambda^y_i}{y_i!}

Distribusi Poisson memiliki parameter $\lambda$ yang menentukan bentuk distribusinya, tetapi $\lambda$ (rata-rata jumlah benih) berbeda untuk setiap individu, dan kita percaya bahwa jumlah benih ditentukan dari distribusi Poisson dengan bentuk yang berbeda untuk setiap individu. Dalam artikel ini, mari kita membangun model statistik untuk tiga pola berikut.

Model statistik di mana jumlah benih tergantung pada ukuran individu
Model statistik di mana jumlah benih tergantung pada ada atau tidaknya perlakuan pemupukan
Model statistik di mana jumlah benih tergantung pada ukuran individu dan ada atau tidaknya perlakuan pemupukan

Model statistik di mana jumlah benih tergantung pada ukuran individu

Pertama-tama, mari kita definisikan $\lambda_i$ sebagai fungsi dari ukuran individu $x_i$ sebagai berikut.

\lambda_i = e^{\beta_1 + \beta_2x_i}

di mana $\beta_1$ dan $\beta_2$ disebut parameter atau koefisien dan $\beta_1$ disebut intersep.

Mengambil logaritma dari kedua sisi, kita mendapatkan

\log (\lambda_i) = \beta_1 + \beta_2 x_i

Sisi kanan $\beta_1 + \beta_2 x_i$ disebut prediktor linier karena merupakan kombinasi linier.

Fungsi di sisi kiri untuk prediktor linier disebut fungsi link. Kali ini fungsi link adalah $\log (\lambda_i)$ dan bersifat logaritmik, sehingga disebut fungsi link log.

Fungsi link log sering digunakan dalam GLM untuk regresi Poisson. Alasannya adalah bahwa rata-rata $\lambda$ dari distribusi Poisson harus non-negatif. Hal ini mudah karena $\lambda_i = e^{linear\_predictor} \geqq 0$ dan itu non-negatif.

Dari sini kita mengestimasi $\beta_1$ dan $\beta_2$ yang memaksimalkan fungsi log-likelihood berikut.

\log L(\beta_1, \beta_2) = \sum_i \log \frac{\lambda_i^{y_i}e^{-\lambda_i}}{y_i!}

Estimasi parameter mudah dilakukan dengan kode Python berikut.

import statsmodels.api as sm
import statsmodels.formula.api as smf

fit_x = smf.glm('y ~ x', data=df, family=sm.families.Poisson()).fit()
fit_x.summary()

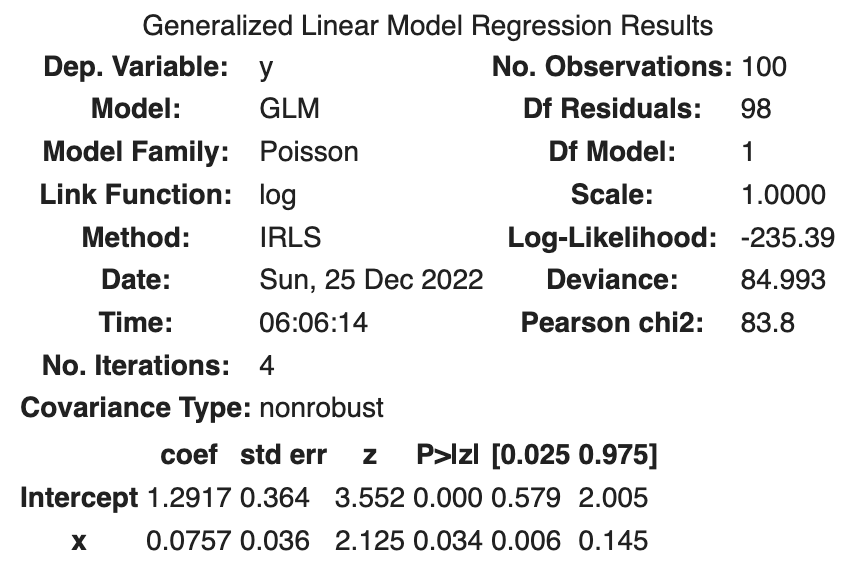
Poisson regression | x

Hasil berikut ini diperoleh.

	coef	std err	z	Log-likelihood
Intercept	1.2917	0.364	3.552
x	0.0757	0.036	2.125
				-235.39

std err adalah standar error, yaitu standar deviasi dari parameter yang diestimasi. Sebuah distribusi normal diasumsikan untuk derivasi standar deviasi. z adalah z-value.

$\lambda$ (rata-rata jumlah biji) adalah sebagai berikut.

\lambda_i = e^{1.2917 + 0.0757x_i}

Plot fungsi di atas.

import numpy as np
import math

sns.scatterplot(x='x', y='y', hue='f', data=df)
x = np.arange(df.x.min(), df.x.max() + 0.01, 0.01)
y = [math.exp(fit_x.params['Intercept'] + fit_x.params['x'] * x_i)  for x_i in x]
plt.plot(x, y)

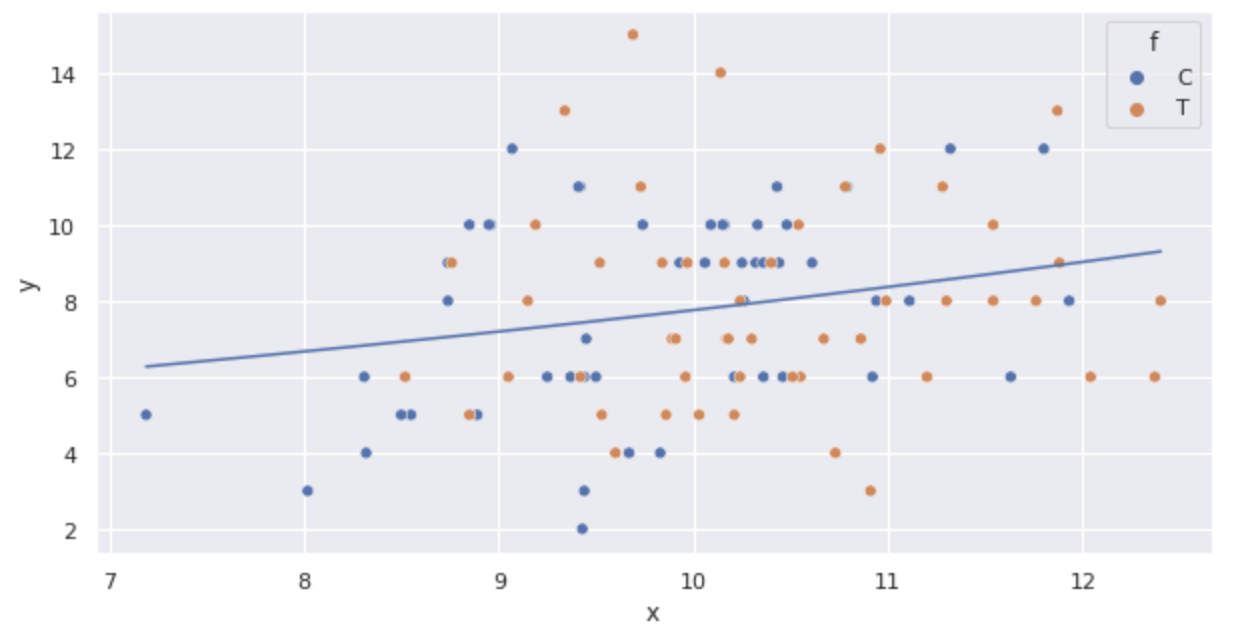
Predict | x

The line is drawn that the average seed count increases as size $x$ increases.

Model statistik di mana jumlah benih tergantung pada ada atau tidaknya perlakuan pemupukan

Mari kita pertimbangkan model yang menggabungkan status aplikasi pupuk $f_i$ sebagai variabel penjelas.

Aplikasi pupuk $f_i$ adalah variabel kategorikal. Variabel kategorikal biasanya digantikan oleh variabel boneka. Aplikasi pupuk $f_i$ digantikan oleh variabel boneka $d_i$ sebagai berikut:

d_i = \left\{ \begin{array}{ll} 0 & (f_i = \mathrm{C}) \\ 1 & (f_i = \mathrm{T}) \end{array} \right.

Modelnya adalah sebagai berikut.

\lambda_i = e^{\beta_1 + \beta_3 d_i}

Artinya, jika individu $i$ tidak memiliki perlakuan pemupukan ( $f_i=C$ ), maka

\lambda_i = e^{\beta_i}

dan jika individu $i$ memiliki perlakuan pemupukan ( $f_i=T$ ), maka

\lambda_i = e^{\beta_i + \beta_3}

Mari kita estimasi $\beta_1$ dan $\beta_2$ yang memaksimalkan fungsi log-likelihood berikut.

\log L(\beta_1, \beta_2) = \sum_i \log \frac{\lambda_i^{y_i}e^{-\lambda_i}}{y_i!}

import statsmodels.api as sm
import statsmodels.formula.api as smf

fit_f = smf.glm('y ~ f', data=df, family=sm.families.Poisson()).fit()
fit_f.summary()

Poisson regression | f

Hasil berikut ini diperoleh.

	coef	std err	z	Log-likelihood
Intercept	2.0516	0.051	40.463
f[T.T]	0.0128	0.071	0.179
				-237.63

Artinya, $\lambda$ (rata-rata jumlah biji) adalah sebagai berikut.

\lambda_i = e^{2.0516} \quad (f_i = \mathrm{C})

\lambda_i = e^{2.0516 + 0.0128} \quad (f_i = \mathrm{T})

Penambahan perlakuan pupuk menghasilkan sedikit peningkatan rata-rata jumlah benih.

Log-likelihoodnya adalah -237,63, yang lebih kecil dari log-likelihood model dengan $x_i$ sebagai variabel penjelas sebesar -235,39. Dengan kata lain, model ini kurang cocok dengan data. Dengan kata lain, model ini kurang cocok dengan data.

Model statistik di mana jumlah benih tergantung pada ukuran individu dan ada atau tidaknya perlakuan pemupukan

Akhirnya, kita mempertimbangkan model yang menggabungkan ukuran $x_i$ dan perlakuan pupuk $f_i$ sebagai variabel penjelas.

Modelnya adalah sebagai berikut

\lambda_i = e^{\beta_1 + \beta_2x_i + \beta_3 d_i}

Estimate $\beta_1$ , $\beta_2$ , and $\beta_3$ that maximize the following log-likelihood functions.

\log L(\beta_1, \beta_2, \beta_3) = \sum_i \log \frac{\lambda_i^{y_i}e^{-\lambda_i}}{y_i!}

import statsmodels.api as sm
import statsmodels.formula.api as smf

fit_full = smf.glm('y ~ x + f', data=df, family=sm.families.Poisson()).fit()
fit_full.summary()

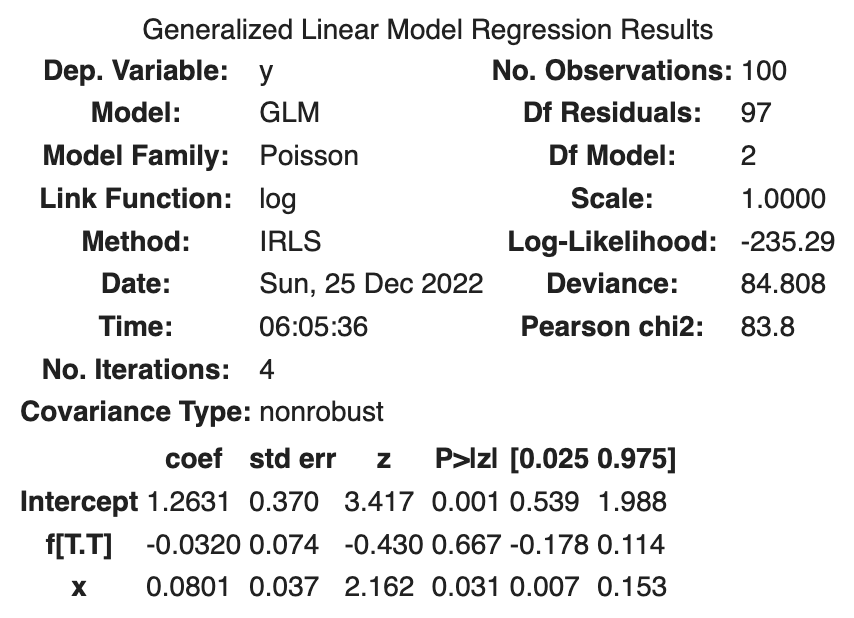
Poisson regression | f

Hasil berikut ini diperoleh.

	coef	std err	z	Log-likelihood
Intercept	1.2631	0.370	3.417
f[T.T]	-0.0320	0.074	-0.430
x	0.0801	0.037	2.162
				-235.29

Hasil berikut ini diperoleh.

\lambda_i = e^{2.0516 + 0.0801 x_i} \quad (f_i = \mathrm{C})

\lambda_i = e^{2.0516 + 0.0801 x_i - 0.0320} \quad (f_i = \mathrm{T})

Hal ini diinterpretasikan bahwa rata-rata jumlah biji akan lebih rendah dengan perlakuan pemupukan. Secara khusus, $e^{-0.032} \approx 0.969$ menunjukkan bahwa rata-rata jumlah benih adalah 0.969 kali lebih tinggi setelah aplikasi pupuk.

Log-likelihood adalah -235,29, yang lebih cocok dengan data daripada dua model sebelumnya.