ロジスティック回帰とは
ロジスティック回帰とは、観察された事象を二項分布で表現するときに使うGLMです。
二項分布のリンク関数はlogitリンク関数がよく使われます。logitリンク関数は次の式の左辺(
ここで、
ロジスティック回帰モデルの構築
実際にロジスティック回帰モデルを構築してみます。ここでは、ある架空の植物100個体の種子数データについて考えます。データは次のカラムで構成されています。
- N: 種子数
- y: 発芽した種子数
- x: 個体のサイズ
- f: 個体に施肥処理をしたかどうか(C: 施肥処理をしていない、T: 施肥処理をしている)
import pandas as pd
# number of seeds
N = [8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,
8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,
8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8,8]
# number of seeds germinated
y = [1,6,5,6,1,1,3,6,0,8,0,2,0,5,3,6,3,4,5,8,5,8,1,4,1,8,4,7,5,5,8,1,7,1,3,8,6,7,
7,4,7,8,8,0,6,5,8,3,8,8,0,5,5,8,3,2,7,8,3,5,8,3,6,7,8,6,5,5,0,8,8,0,6,1,8,8,
6,6,6,6,8,8,7,8,6,2,0,7,8,8,8,3,7,8,8,7,0,5,8,1]
# body size
x = [9.76,10.48,10.83,10.94,9.37,8.81,9.49,11.02,7.97,11.55,9.46,9.47,8.71,10.42,10.06,
11,9.95,9.52,10.26,11.33,9.77,10.59,9.35,10,9.53,12.06,9.68,11.32,10.48,10.37,11.33,
9.42,10.68,7.91,9.39,11.65,10.66,11.23,10.57,10.42,11.73,12.02,11.55,8.58,11.08,10.49,
11.12,8.99,10.08,10.8,7.83,8.88,9.74,9.98,8.46,7.96,9.78,11.93,9.04,10.14,11.01,8.88,
9.68,9.8,10.76,9.81,8.37,9.38,7.68,10.23,9.83,7.66,9.33,8.2,9.54,10.55,9.88,9.34,10.38,
9.63,12.44,10.17,9.29,11.17,9.13,8.79,8.19,10.25,11.3,10.84,10.97,8.6,9.91,11.38,10.39,
10.45,8.94,8.94,10.14,8.5]
# feed (C: control, T: treatment)
f = ['C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
'C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C','C',
'C','C','C','C','C','C','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
'T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T','T',
'T','T','T','T','T','T','T','T','T','T','T','T']
df = pd.DataFrame(list(zip(N, y, x, f)), columns =['N', 'y', 'x', 'f'])
display(df.head())
| N | y | x | f | |
|---|---|---|---|---|
| 0 | 8 | 1 | 9.76 | C |
| 1 | 8 | 6 | 10.48 | C |
| 2 | 8 | 5 | 10.83 | C |
| 3 | 8 | 6 | 10.94 | C |
| 4 | 8 | 1 | 9.37 | C |
データの確認
記述統計量を確認します。
df.describe()
| N | y | x | |
|---|---|---|---|
| count | 100.0 | 100.000000 | 100.000000 |
| mean | 8.0 | 5.080000 | 9.967200 |
| std | 0.0 | 2.743882 | 1.088954 |
| min | 8.0 | 0.000000 | 7.660000 |
| 25% | 8.0 | 3.000000 | 9.337500 |
| 50% | 8.0 | 6.000000 | 9.965000 |
| 75% | 8.0 | 8.000000 | 10.770000 |
| max | 8.0 | 8.000000 | 12.440000 |
fについてC、Tの数をそれぞれ表示します。
print('num of C:', len(df[df['f'] == 'C']))
print('num of T:', len(df[df['f'] == 'T']))
num of C: 50
num of T: 50
データの記述統計量から次のことが確認できます。
- 種子数N:
- 全て8でとなっている
- 発芽した種子数y:
- 非負の整数となっている(0から8)
- 個体サイズx:
- 正の実数(連続値)となっている
- 分散は小さい
- 施肥処理の有無f:
- カテゴリ変数となっている
- 各カテゴリの要素数は均等になっている
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
plt.style.use('ggplot')
plt.figure(figsize=(10,5))
sns.set(rc={'figure.figsize':(10,5)})
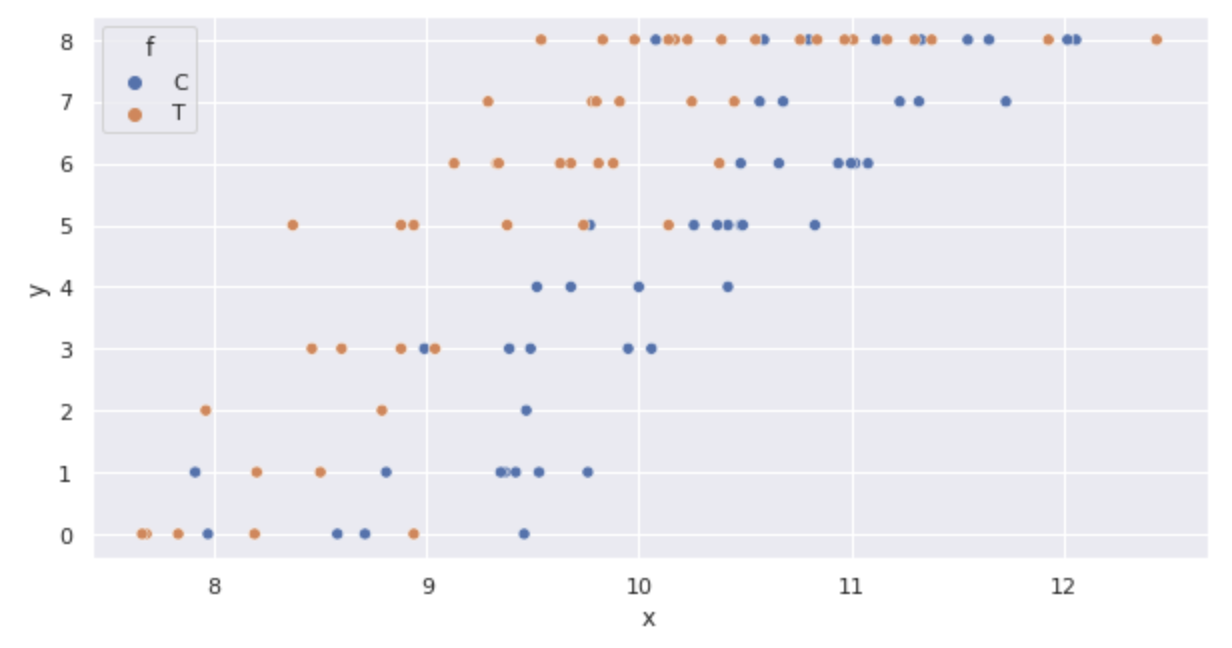
sns.scatterplot(x='x', y='y', hue='f', data=df)
箱ヒゲ図を表示します。
sns.boxplot(x='f', y='y', data=df)
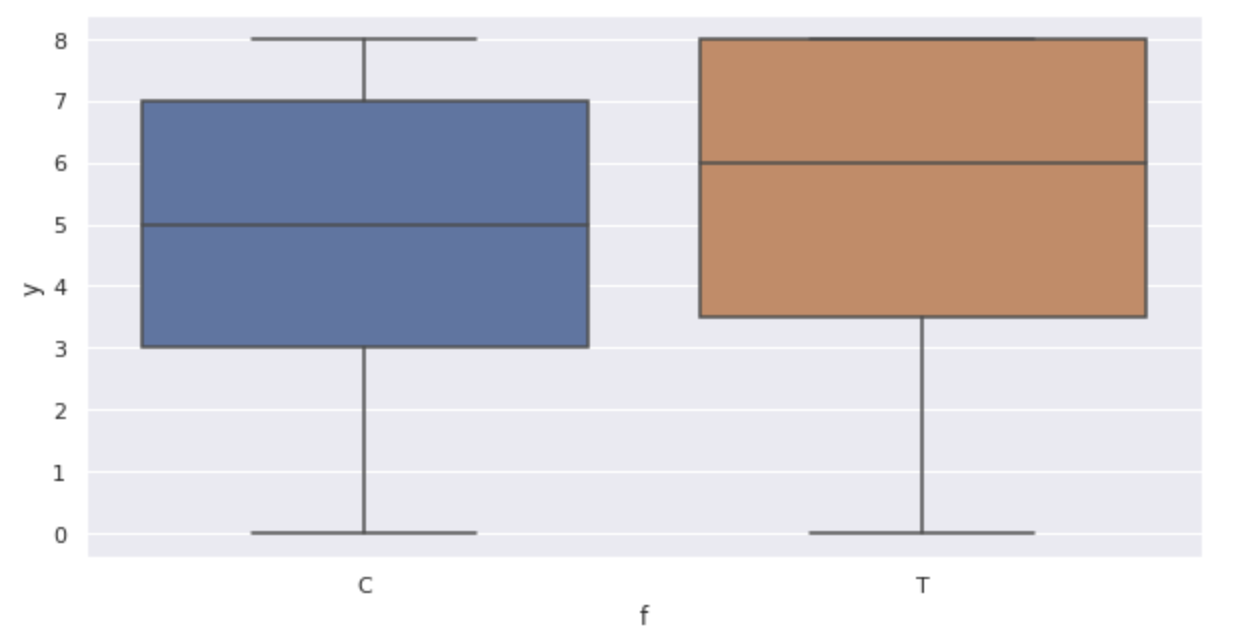
グラフから次のことが確認できます。
- サイズ
x - 肥料を行うと発芽した種子数yも増加している(箱ヒゲ図)
モデルの構築
データの
二項分布は次の式で表されます。
このときに個体
確率を表現するときによく使われる関数にロジスティック関数があります。ロジスティック関数は次の式で表されます。
ロジスティック関数を図示すると次のようになります。
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
%matplotlib inline
plt.style.use('ggplot')
plt.figure(figsize=(10,5))
x = np.arange(-10, 10, 0.01)
y = [ 1 / ( 1 + math.exp(-x_i)) for x_i in x]
plt.plot(x, y, color='black', label='logsitic function')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.show()
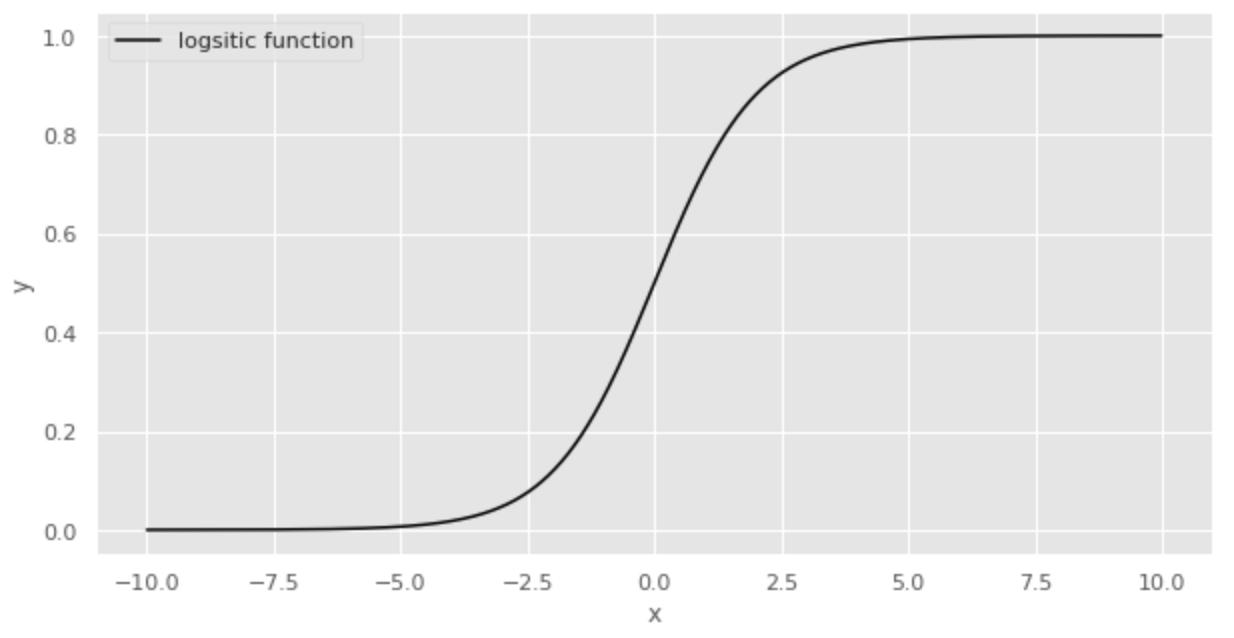
ロジスティック関数はyが0から1の範囲となり、xが0のときに0.5となります。このような性質から、ロジスティック関数は確率を表現するのに適している関数となります。
ロジスティック関数を今回の変数に置き換えると次の式になります。
ここで、
上式の左辺は logit リンク関数と呼ばれています。logitリンク関数は、ロジスティック関数の逆関数となっています。
種子の発芽確率
つまり、発芽確率
したがって、次の対数尤度関数を最大化する
パラメータ推定
import statsmodels.api as sm
import statsmodels.formula.api as smf
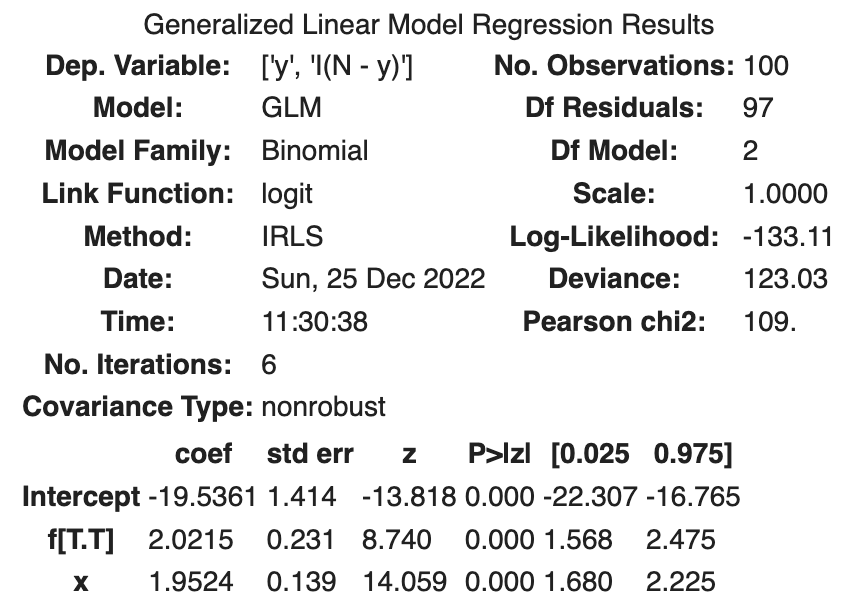
fit_xf = smf.glm(formula='y + I(N - y) ~ x + f', data=df, family=sm.families.Binomial()).fit()
fit_xf.summary()
# aic
fit_xf.aic
次の結果が得られました。
| coef | std err | z | Log-likelihood | AIC | |
|---|---|---|---|---|---|
| Intercept | -19.5361 | 1.414 | -13.818 | ||
| f[T.T] | 2.0215 | 0.231 | 8.740 | ||
| x | 1.9524 | 0.139 | 14.059 | ||
| -133.11 | 272.21 |
推定したパラメータをロジスティック回帰モデルに代入し、図示してみます。
import numpy as np
import math
sns.scatterplot(x='x', y='y', hue='f', data=df)
x = np.arange(df.x.min(), df.x.max() + 0.01, 0.01)
y_T = [8 * 1 / ( 1 + math.exp(-(fit_xf.params['Intercept'] + fit_xf.params['x'] * x_i + fit_xf.params['f[T.T]']))) for x_i in x]
y_C = [8 * 1 / ( 1 + math.exp(-(fit_xf.params['Intercept'] + fit_xf.params['x'] * x_i))) for x_i in x]
plt.plot(x, y_T, color='black', label='logsitic T')
plt.plot(x, y_C, color='gray', label='logsitic C')
plt.legend()
plt.show()
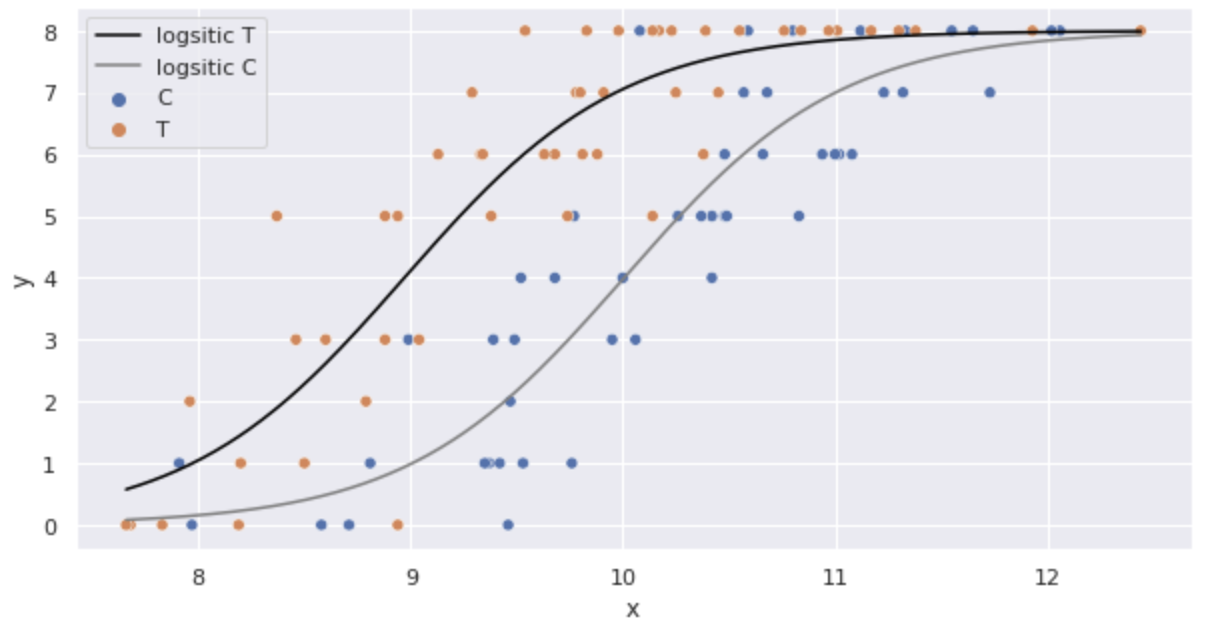
良いモデルが作れているように見えます。
logit の解釈
logitリンク関数を次のように変形してみます。
左辺の
そしてこのオッズは
施肥処理をすると施肥処理しない場合と比較してオッズが7.5倍になるということになります。
logitリンク関数の定義は
参考