Apa itu model statistik

Model statistik adalah model matematika yang menjelaskan pola atau hukum tentang data yang diamati. Model ini memilih distribusi probabilitas sesuai dengan karakteristik data dan mengestimasi parameter distribusi probabilitas yang dapat menjelaskan data yang diamati dengan baik.

Estimasi parameter

Saya akan melakukan estimasi parameter dalam Python untuk data sampel berikut dengan ukuran sampel 50.

data = [2,2,4,6,4,5,2,3,1,2,0,4,3,3,3,3,4,2,7,2,4,3,3,3,4,
        3,7,5,3,1,7,6,4,6,5,2,4,7,2,2,6,2,4,5,4,5,1,3,2,3]

Investigasi data

Pertama, mari kita lihat histogram dari data.

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

data = [2,2,4,6,4,5,2,3,1,2,0,4,3,3,3,3,4,2,7,2,4,3,3,3,4,
        3,7,5,3,1,7,6,4,6,5,2,4,7,2,2,6,2,4,5,4,5,1,3,2,3]

plt.hist(data, bins = [-0.5 + v for v in range(max(data) + 2)], alpha=0.5, rwidth=0.95)
plt.xlabel('data')
plt.ylabel('Frequency')

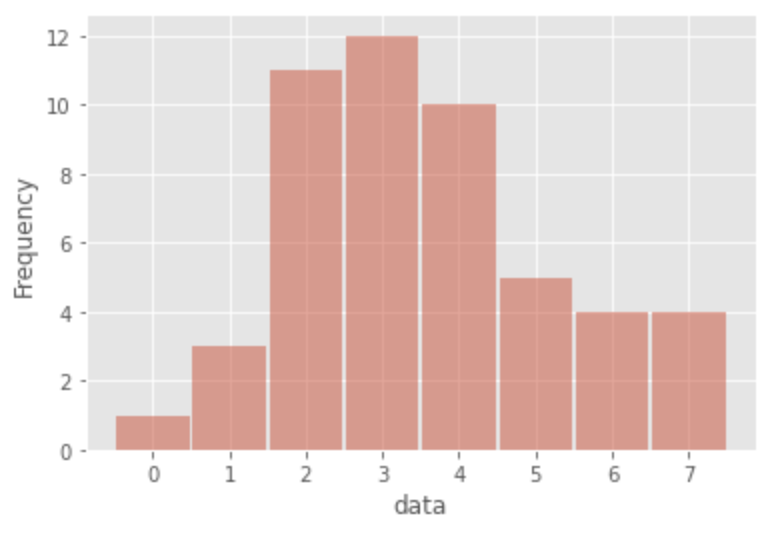
Berikutnya mari kita lihat ringkasan data.

import pandas as pd

df = pd.DataFrame(data, columns=['x'])
df.describe()

Mari kita lihat varians sampel.

# sample variabce
df.var()

2.986122

Survei ini mengonfirmasi hal-hal berikut ini:

• Distribusi seperti gunung
• Data adalah data hitungan (bilangan bulat non-negatif)
• Rata-rata sampel adalah 3,56
• Varians sampel adalah 2,99

Asumsi distribusi probabilitas

Dari data sampel, kita asumsikan distribusi probabilitas yang diikuti oleh populasi. Kita mengetahui hal-hal berikut ini tentang data sampel.

• Data adalah data hitungan
• Batas bawah adalah 0 tetapi batas atas tidak diketahui
• Rata-rata sampel adalah 3,56 dan varians sampel adalah 2,99, yang relatif dekat

Dari karakteristik di atas, kita asumsikan sebuah [distribusi Poisson] (/en/articles/poisson-distribution) dengan \lambda=3.56.

Distribusi Poisson vs. distribusi sampel

Visualisasikan distribusi Poisson dari \lambda=3.56 dan distribusi data sampel yang ditumpangkan.

fig, ax1 = plt.subplots()
plt.hist(data, bins = [-0.5 + v for v in range(max(data) + 2)], alpha=0.5, rwidth=0.95)
poisson_values = poisson.rvs(3.56, size=10000)
prod = (pd.value_counts(poisson_values) / 10000).sort_index()
ax2 = ax1.twinx()
ax2.plot(prod)
plt.show()

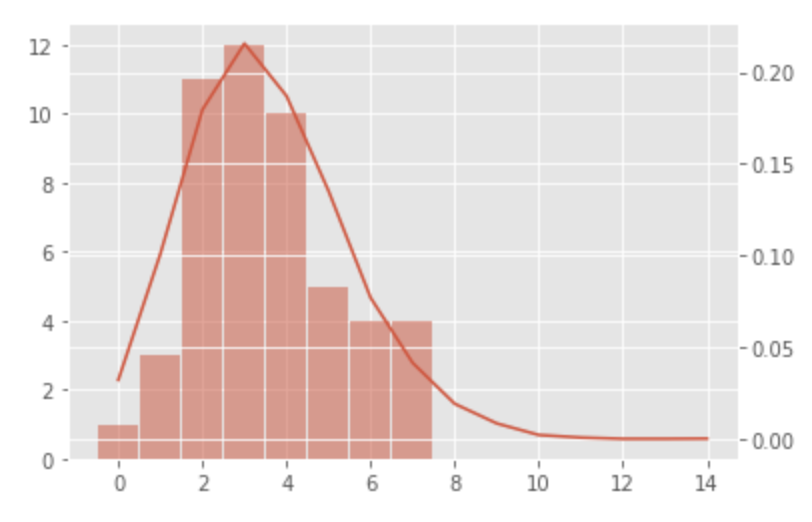
Tampak bahwa distribusi data sampel dapat diwakili oleh distribusi Poisson dengan \lambda=3.56.

Estimasi parameter dari distribusi probabilitas yang diasumsikan

Parameter distribusi probabilitas diestimasi berdasarkan data sampel. Di sini kita menggunakan metode estimasi parameter yang disebut maximum likelihood estimation.

Maximum likelihood estimation adalah metode estimasi parameter yang mencari parameter yang memaksimalkan likelihood, sebuah statistik yang menyatakan seberapa baik parameter tersebut sesuai dengan data yang diamati. Dalam hal ini, parameternya adalah \lambda. Dengan kata lain, kita mengestimasi nilai \lambda yang memaksimalkan kecocokan dengan data.

Likelihood adalah hasil kali dari probabilitas untuk semua data sampel. Likelihood adalah fungsi dari parameter, dilambangkan dengan L. Karena parameter dalam kasus ini adalah \lambda, maka ekspresi untuk likelihood adalah sebagai berikut

di mana y_i adalah nilai yang diamati. Dalam contoh ini, y_1=2, y_2=2, y_3=4, \cdots, y_{50}=3.

Kita memeriksa \lambda yang memaksimalkan likelihood L(\lambda). Namun, karena likelihood seperti itu bersifat multiplikatif dan sulit ditangani, log-transformed log-likelihood digunakan untuk estimasi likelihood maksimum dari parameter.

Gambar berikut ini menunjukkan bentuk distribusi dan nilai log L(\lambda) ketika parameter \lambda divariasikan dari 3,2 sampai 4,4.

import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
import sympy
from scipy.stats import poisson
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

lams = np.arange(3.2,4.5,0.4)

for i, lam in enumerate(lams):
    log_l = 0
    for y in data:
        f = (lam**y)*sympy.exp(-lam)/sympy.factorial(y)
        logf=sympy.log(f)
        log_l = log_l + logf

    fig, ax = plt.subplots()
    ax.hist(data, bins = [-0.5 + v for v in range(max(data) + 2)], alpha=0.5, rwidth=0.95)
    poisson_values = poisson.rvs(lam, size=10000)
    prod = (pd.value_counts(poisson_values) / 10000).sort_index()
    ax2 = ax.twinx()
    ax2.plot(prod, label=f'lambda={round(lam, 1)}, log L={round(log_l, 1)}')
    plt.legend()
    plt.show()

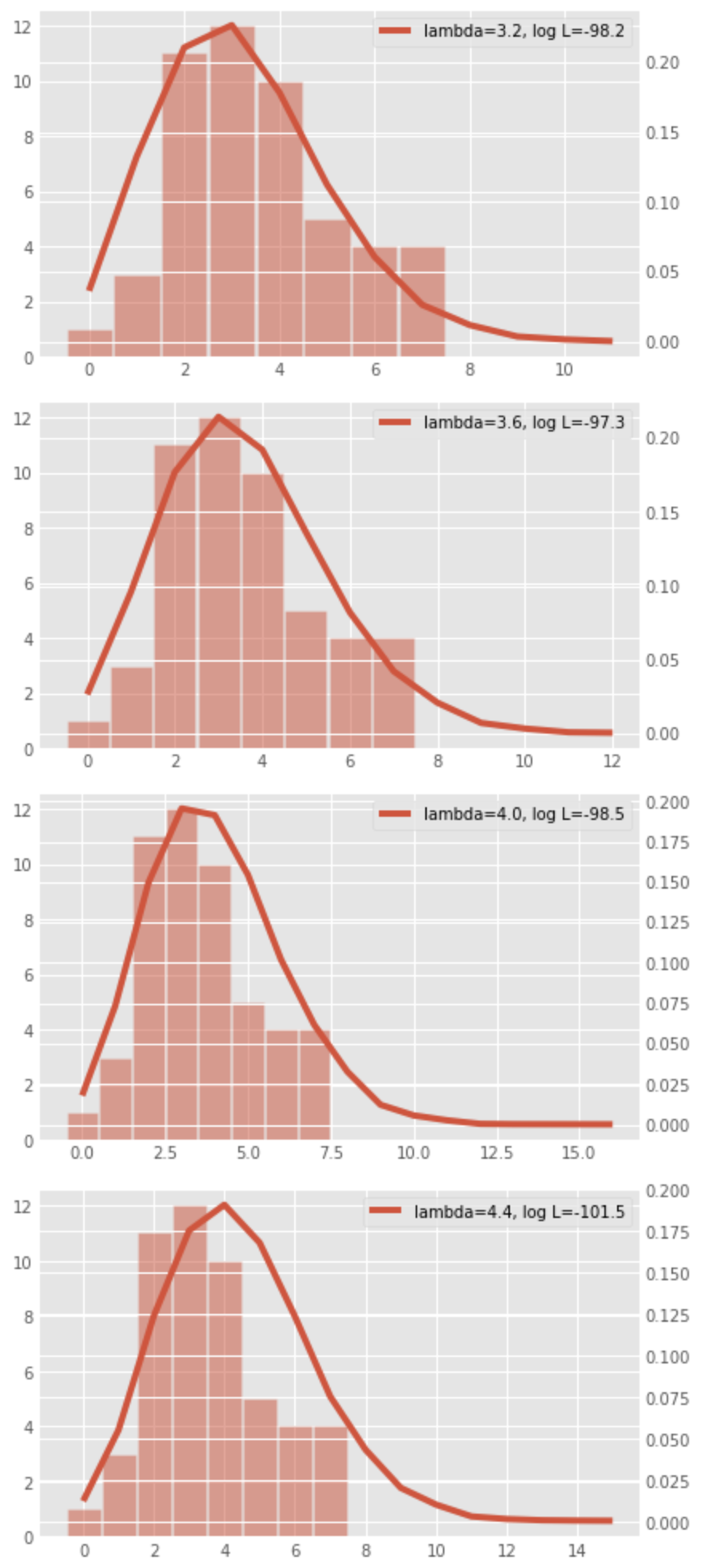
Kita dapat melihat bahwa log-likelihood kemungkinan akan dimaksimalkan di sekitar \lambda=3.6. Karena log L adalah fungsi yang meningkat secara monoton dari likelihood L, maka log likelihood juga maksimum pada \lambda dimana log likelihood maksimum.

Untuk memperoleh log likelihood maksimum, kita dapat menemukan \lambda dimana turunan parsial dari log likelihood dengan parameter \lambda adalah 0.

Menghitung persamaan di atas, kita melihat bahwa kemungkinan dimaksimalkan ketika \lambda=3.56.

Distribusi probabilitas mana yang harus digunakan untuk model statistik

Ketika memilih distribusi probabilitas untuk model statistik untuk menjelaskan data yang diamati, poin-poin berikut perlu diperiksa:

• Jenis data (diskrit atau kontinu)
• Rentang data
• Hubungan antara varians sampel dan rata-rata sampel

Untuk beberapa distribusi probabilitas, kondisi yang diperlukan yang dapat digunakan sebagai distribusi probabilitas untuk model statistik adalah sebagai berikut.