2022-11-22

リッジ回帰

Machine Learning

Regression

Python

sklearn

リッジ回帰とは

リッジ回帰は、L2正則化としても知られる、線形回帰モデルにおける多重共線性の問題を解決するための正則化技術です。予測変数が高度に相関している場合、回帰係数の不安定で信頼性の低い推定値が得られることがあります。目的関数にペナルティ項を組み込むことで、リッジ回帰は回帰係数を縮小し、より安定かつ堅牢なモデルを得ることができます。

数学的基礎

コスト関数

線形回帰では、入力特徴量（独立変数）と目的変数（従属変数）の関係をデータに合わせて線形関数でフィッティングすることを目指します。コスト関数は、予測値と実際値の誤差を測定するために使用されます。線形回帰においてもっとも一般的に使用されるコスト関数は、平均二乗誤差（MSE）関数です。

J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2

$m$ はトレーニング例の数
$h_\theta(x^{(i)})$ は $i$ 番目の例に対する予測値
$y^{(i)}$ は $i$ 番目の例に対する実際の値
$\theta$ はモデルのパラメータベクトル

目標は、コスト関数 $J(\theta)$ を最小化することであり、つまり、最小の誤差をもたらす $\theta$ の最適な値を見つけることです。

L2ペナルティ項

リッジ回帰では、コスト関数にL2ペナルティ項を追加して、大きなパラメータ値にペナルティを与えます。この正則化項は、モデルの複雑さを制限することで過学習を防止するのに役立ちます。L2ペナルティ項は次のように定義されます。

\Omega(\theta) = \lambda \sum_{j=1}^n \theta_j^2

ここで、

$\lambda$ は正則化パラメータ（リッジ係数とも呼ばれます）で、正則化の強度を制御する
$n$ は特徴量の数（バイアス項を除く）
$\theta_j$ は、パラメータベクトル $\theta$ の $j$ 番目のパラメータ

L2ペナルティ項を加えたリッジ回帰のコスト関数は次のようになります。

J(\theta) = \frac{1}{2m} \sum_{i=1}^m (h_\theta(x^{(i)}) - y^{(i)})^2 + \lambda \sum_{j=1}^n \theta_j^2

この変更されたコスト関数 $J(\theta)$ を最小化することで、パラメータ $\theta$ の最適な値を見つけることが目的です。 $\lambda$ が増加するにつれて、ペナルティ項はコスト関数に強い影響を与え、バイアスが高く分散が低いモデルを得ることができます。逆に、 $\lambda$ が減少するにつれて、ペナルティ項は弱くなり、バイアスが低く分散が高いモデルを得ることができます。

Pythonによるリッジ回帰の実装

この章では、California住宅データセットを使用して、Pythonでリッジ回帰の実装を示します。正則化パラメータを変化させた線形回帰とリッジ回帰の結果をプロットして、モデルへの影響を解釈します。

まず、必要なライブラリをインポートします。

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.metrics import mean_squared_error

次に、California住宅データセットをロードし、トレーニングセットとテストセットに分割し、特徴量をスケーリングする前処理を行います。

python

# Load the dataset
data = fetch_california_housing()
X, y = data['data'], data['target']

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Scale the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

次に、正則化パラメータを変化させた線形回帰とリッジ回帰の両方のモデルを適合させ、パフォーマンスを比較します。

python

# Initialize models
linear_regression = LinearRegression()
ridge_regressions = [Ridge(alpha=alpha) for alpha in np.logspace(-3, 3, 7)]

# Fit models
linear_regression.fit(X_train_scaled, y_train)
for ridge_regression in ridge_regressions:
    ridge_regression.fit(X_train_scaled, y_train)

最後に、平均二乗誤差（MSE）を使用してモデルを評価し、結果を可視化するためのプロットを作成します。

python

# Evaluate models
mse_linear_regression = mean_squared_error(y_test, linear_regression.predict(X_test_scaled))
mse_ridge_regressions = [mean_squared_error(y_test, ridge_regression.predict(X_test_scaled)) for ridge_regression in ridge_regressions]

# Set up the plot
plt.figure(figsize=(10, 6))
sns.set(style="whitegrid")
plt.xscale("log")
plt.xlabel("Regularization Parameter (alpha)")
plt.ylabel("Mean Squared Error")
plt.title("Linear Regression vs Ridge Regression")

# Plot the results
plt.plot(np.logspace(-3, 3, 7), [mse_linear_regression] * 7, label="Linear Regression", linestyle="--", marker="o", color="blue")
plt.plot(np.logspace(-3, 3, 7), mse_ridge_regressions, label="Ridge Regression", linestyle="--", marker="o", color="red")
plt.legend()

# Show the plot
plt.show()

MSE

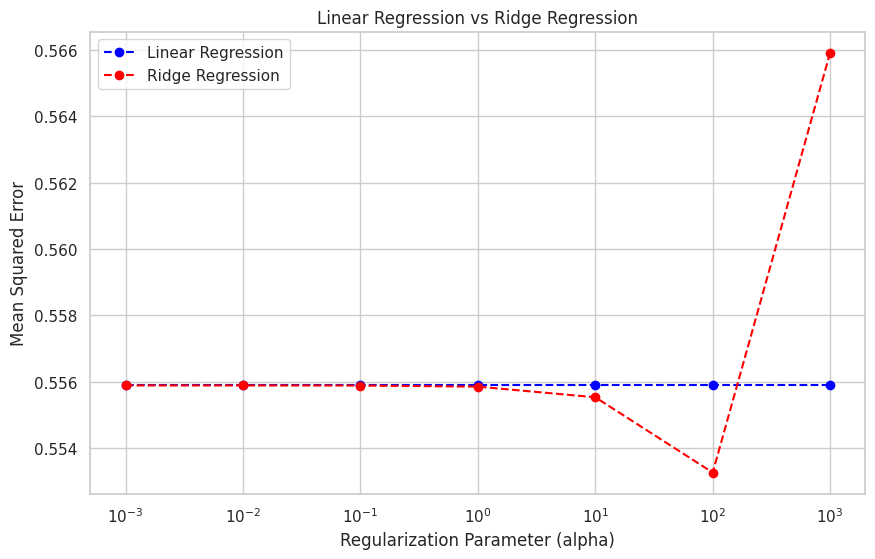
このプロットは、異なる正則化パラメータに対する線形回帰とリッジ回帰モデルの平均二乗誤差を示しています。正則化パラメータ（alpha）が増加するにつれて、リッジ回帰モデルのパフォーマンスが向上し、最初は線形回帰モデルを上回ります。しかし、alphaがあまりにも大きくなると、係数の過剰な縮小により、リッジ回帰モデルのパフォーマンスが低下することがあります。

リッジ回帰

リッジ回帰とは

数学的基礎

コスト関数

L2ペナルティ項

Pythonによるリッジ回帰の実装

ラッソ回帰

K-最近傍法（KNN）回帰

Ryusei Kakujo