2022-11-22

K-最近傍法（KNN）回帰

Machine Learning

Regression

Python

sklearn

K-最近傍法（KNN）回帰とは

K-最近傍法（KNN）回帰は、連続的な目的変数の予測に使用されるノンパラメトリックな教師あり学習アルゴリズムです。パラメトリックモデルとは異なり、KNN回帰は基盤となるデータ分布や変数間の関係についての仮定を行いません。代わりに、距離メトリックによって測定される近接度で、近くの観測値の平均を取ることによって目的変数を推定します。KNN回帰は、複雑な非線形関係をモデル化できるシンプルで強力なアルゴリズムです。

適切な「K」の選択

「K」の選択は、KNNアルゴリズムの性能に影響を与える重要な要因です。「K」の値が小さい場合、データの局所的なパターンを捉えるより複雑なモデルが生成されますが、ノイズに敏感で過学習につながる可能性があります。一方、「K」の値が大きい場合、ノイズに対して感度が低くなるより一般的なモデルが生成されますが、重要な局所的なパターンを見逃し、適合不足につながる可能性があります。「K」の適切な値の選択は、クロスバリデーションや実験によって達成できます。

線形回帰との比較

線形回帰とKNN回帰の主な違いは次のとおりです。

モデルの仮定
線形回帰は、独立変数と従属変数の間に線形関係があると仮定し、データ点を最適にフィットする直線を見つけようとします。一方、KNN回帰は、データの分布や変数間の関係について仮定を行わない非パラメトリックな方法であるため、より柔軟で複雑な非線形関係をモデル化することができます。
モデルの複雑さ
線形回帰は、直線（または複数の独立変数の場合は超平面）で表されるシンプルで解釈しやすいモデルを生成します。KNN回帰は、「K」の選択と距離メトリックによって複雑なモデルを生成することができます。この柔軟性は、特定の状況では有利になる場合がありますが、小さい「K」値の場合に特に過学習に陥る可能性があるため、モデルをより適合させる必要があります。
特徴量のスケーリング
線形回帰は、各特徴量に対して係数を独立に推定するため、特徴量のスケールに対して感度が低くなります。一方、KNN回帰は、最近傍点を見つけるために距離メトリックを使用するため、特徴量のスケールに対して感度が高くなります。そのため、KNN回帰においては特徴量のスケーリング（例えば、正規化や標準化）が必要な前処理ステップです。
学習と予測時間
線形回帰は、計算効率が良い閉形式の解が存在するため、学習プロセスが比較的高速です。係数が推定されると、予測も迅速に行えます。一方、KNN回帰は明示的な学習フェーズがなく、予測に必要な全てのトレーニングデータを保存するため、予測時間が長くなる可能性があります。特に、大規模なデータセットでは、KNN回帰の予測時間が大幅に遅くなる可能性があります。
外れ値の取り扱い
線形回帰は、データの外れ値に敏感であり、推定係数やモデルの性能に大きな影響を与えることがあります。一方、KNN回帰は、適切な「K」の選択により、複数の近傍点を考慮して予測を行うため、外れ値に対して一般的にロバストなモデルです。

PythonによるKNN回帰の実装

この章では、California Housingデータセットを使用してPythonでKNN回帰を実装する方法を説明します。また、「K」の値を変化させることの効果を探求し、クロスバリデーションを通じて最適な「K」を選択します。

まず、必要なライブラリをインポートします。

python

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import mean_squared_error

Housingデータセットをロードし、基本的な前処理を実行します。

python

# Load the California Housing dataset
california_housing = datasets.fetch_california_housing()
X = california_housing.data
y = california_housing.target

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Scale the features
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
X_test_scaled = scaler.transform(X_test)

次に、KNN回帰モデルを実装し、クロスバリデーションを使用してパフォーマンスを評価します。

python

# Initialize a range of K values
k_values = np.arange(1, 31)

# Perform GridSearchCV to find the best K value
knn_regressor = KNeighborsRegressor()
param_grid = {'n_neighbors': k_values}
grid_search = GridSearchCV(knn_regressor, param_grid, cv=5, scoring='neg_mean_squared_error', n_jobs=-1)
grid_search.fit(X_train_scaled, y_train)

# Obtain the best K value and corresponding performance
best_k = grid_search.best_params_['n_neighbors']
best_performance = -grid_search.best_score_
print(f"Best K value: {best_k}")
print(f"Best performance (Mean Squared Error): {best_performance}")

最後に、Kの値を変化させたKNN回帰のパフォーマンスを示すグラフを作成します。

python

# Retrieve the performance for each K value
performance = -grid_search.cv_results_['mean_test_score']

# Set up the plotting environment
sns.set(style="darkgrid")
plt.figure(figsize=(10, 6))

# Plot the performance for each K value
plt.plot(k_values, performance, marker='o', linestyle='-', linewidth=2)
plt.xlabel("Number of Neighbors (K)")
plt.ylabel("Mean Squared Error")
plt.title("KNN Regression Performance with Various K")

# Highlight the best K value
plt.scatter(best_k, best_performance, s=200, c='red', marker='x', zorder=5)
plt.annotate(f"Best K: {best_k}",
             xy=(best_k, best_performance),
             xytext=(best_k + 2, best_performance),
             arrowprops=dict(facecolor='black', arrowstyle='->'))

plt.show()

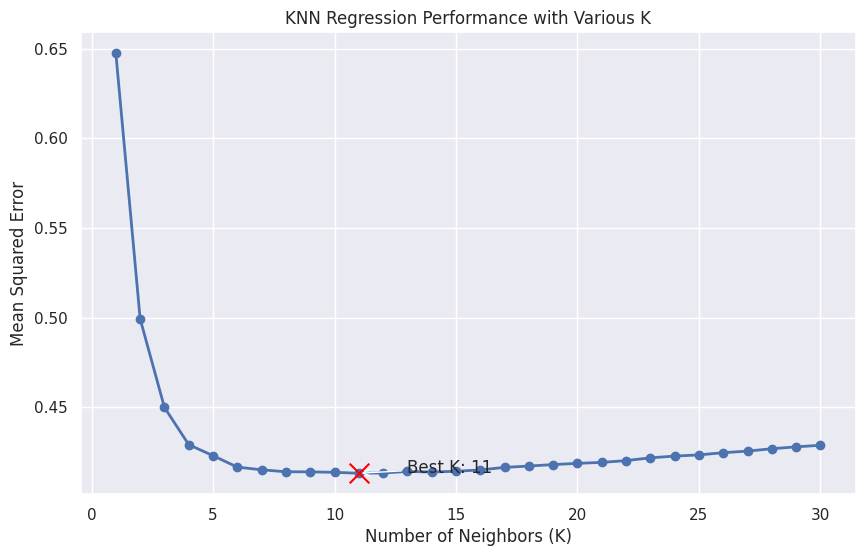
KNN Regression Performance with Various K

このグラフは、異なるKの値に対するKNN回帰のパフォーマンスを示し、最適なKの値が赤で強調表示されています。Kが変化するにつれて過学習と適合不足のトレードオフを視覚化するため、モデルの最適な値を選択するのがより容易になります。

Kの値によるKNN回帰の予測を可視化するために、まずCalifornia Housingデータセットから1つの特徴を選択します。可視化の目的で、最初の列にある「MedInc」（中央値の収入）特徴を使用します。次に、実際のターゲット値の散布図を作成し、異なるK値のKNN回帰予測を重ね合わせます。

python

# Extract the 'MedInc' feature for visualization
X_medinc = X_train_scaled[:, 0].reshape(-1, 1)

# Generate a range of 'MedInc' values for plotting
medinc_range = np.linspace(X_medinc.min(), X_medinc.max(), 100).reshape(-1, 1)

# Set up the plotting environment
sns.set(style="darkgrid")
plt.figure(figsize=(12, 8))

# Create a scatterplot of the actual target values
plt.scatter(X_medinc, y_train, s=15, c='gray', label='Actual Data')

# Overlay the KNN Regression predictions for various K values
k_values_to_plot = [1, 5, 10, 20, best_k]
colors = ['red', 'blue', 'green', 'purple', 'orange']
for k, color in zip(k_values_to_plot, colors):
    knn_regressor = KNeighborsRegressor(n_neighbors=k)
    knn_regressor.fit(X_medinc, y_train)
    predictions = knn_regressor.predict(medinc_range)
    plt.plot(medinc_range, predictions, linestyle='-', color=color, label=f'K={k}')

# Customize the plot appearance
plt.xlabel("Median Income (Normalized)")
plt.ylabel("Median House Value")
plt.title("KNN Regression with Various K")
plt.legend()
plt.show()

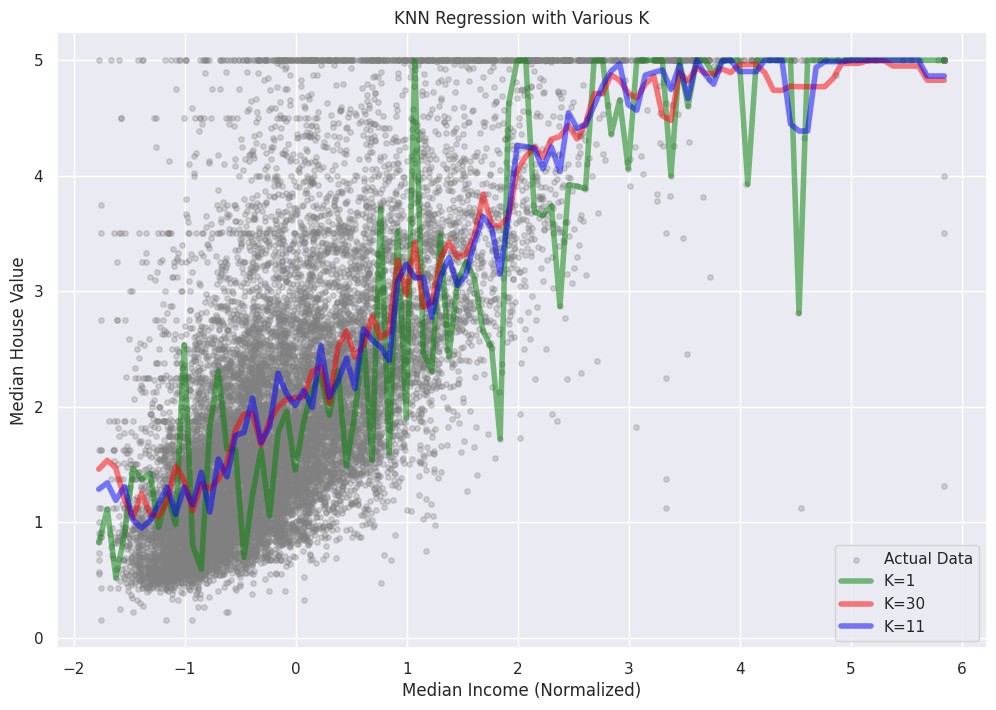
KNN Regression with Various K

このプロットでは、KNN回帰予測が異なるK値に対してどのように変化するかを示しています。Kが増加するにつれて、モデルはより滑らかになり、個々のデータポイントに対してより感度が低くなり、過学習のリスクが低下します。しかし、適切なKの値を選択することが重要であり、データの根本的なパターンを捉え、過学習または適合不足を避けるためのバランスを取る必要があります。

K-最近傍法（KNN）回帰

K-最近傍法（KNN）回帰とは

適切な「K」の選択

線形回帰との比較

PythonによるKNN回帰の実装

参考

リッジ回帰

多項式回帰

Ryusei Kakujo