正則化とは
正則化とは、機械学習や統計モデリングにおいて、損失関数にペナルティ項を追加することでモデルの複雑さを減らす技術です。このペナルティ項により、過学習を防止し、未知のデータでもモデルがうまく汎化できるようになります。つまり、正則化は、モデルがデータ内の複雑なパターンを学習しすぎることと、学習不足のバランスをとるのに役立ちます。
機械学習における正則化の重要性
機械学習において、正則化は次のような理由から重要な役割を担っています。
-
過学習防止
過学習は、モデルがトレーニングデータ内のノイズを学習することで、未知のデータでは性能が低下する現象です。正則化は、複雑なモデルにペナルティを課すことで、シンプルなモデルを促し、過学習を防止するのに役立ちます。 -
特徴量選択
L1正則化などの一部の正則化技術は、いくつかの係数をゼロに縮小することでモデルのスパーシティを促進し、特徴量選択を実行します。これにより、モデルは解釈性と堅牢性が向上します。 -
安定性
L2正則化などの正則化技術は、入力データの小さな変化に対してモデルの係数が敏感になるのを防ぎ、モデルの安定性を高めることができます。 -
モデルの複雑さの減少
正則化により、モデルの容量が制限され、より簡単で解釈性が高く、メンテナンスが容易なモデルが作成されます。
過学習と学習不足
機械学習において、最終的な目標は、未知のデータでもうまく汎化できるモデルを構築することです。ただし、モデル構築プロセスには、過学習と学習不足という2つの一般的な課題が生じます。どちらも、新しいデータに対するモデルの性能に悪影響を与える可能性があります。
-
過学習
過学習は、モデルがトレーニングデータ内のノイズやランダムな変動を学習することで、根本的なパターンを捉えることができず、トレーニングデータに対しては非常に高い性能を示しますが、未知のデータに対しては性能が低下する現象です。過学習は、モデルが複雑で分散が高い場合に生じます。 -
学習不足
学習不足は、モデルがデータ内の根本的なパターンを捉えるのに十分な複雑さを持っていない場合に生じます。その結果、モデルはトレーニングデータと未知のデータの両方で性能が低下します。学習不足は、モデルに高いバイアスがある場合に生じます。
L1正則化(Lasso)
L1正則化は、Lasso(Least Absolute Shrinkage and Selection Operator)としても知られており、モデルの係数の絶対値を損失関数に追加する正則化技術です。L1正則化による変更された損失関数は、次のように表されます。
ここで、
L1正則化により、いくつかの係数をゼロに縮小することで、モデルのスパーシティを促進し、特徴量選択を実行できます。これにより、より解釈性が高く、よりシンプルなモデルが得られます。
メリット
-
特徴量選択
L1正則化は、特徴量選択を実行できるため、モデルをより解釈性が高く、堅牢性が高くなります。 -
モデルのシンプルさ
モデルの係数のスパーシティを促進することで、L1正則化は、よりシンプルで解釈性が高く、維持しやすいモデルを生成します。
デメリット
-
不安定性
特徴間に高い多重共線性が存在する場合、L1正則化は不安定な解を導く可能性があります。多重共線性が存在するグループの中から1つの特徴量しか選択しない傾向があるためです。 -
小規模データには不適切
L1正則化は、スパースな性質により、小規模データでは追加のバイアスを導入する可能性があるため、性能が低下することがあります。
L2正則化(Ridge)
L2正則化は、Ridgeとしても知られている別の一般的な正則化技術で、モデルの係数の2乗を損失関数に追加します。L2正則化による変更された損失関数は、次のように表されます。
ここで、
L2正則化は、全ての特徴を使用するようにモデルを促進しますが、小さい係数で使用するようにして、過学習を減らし、安定性を促進します。
メリット
-
安定性
L2正則化は、L1正則化よりも安定性が高く、特徴量間に多重共線性がある場合に効果的であるため、多重共線性がある場合にも適しています。 -
バイアスが小さい
L2正則化は、L1正則化に比べてモデルにバイアスを導入する可能性が低いため、小規模データに適している場合があります。
デメリット
-
特徴量選択ができない
L2正則化は、L1正則化とは異なり、モデルの係数のスパーシティを促進せず、したがって特徴量選択を行いません。 -
モデルの解釈性が低い
L2正則化はスパース性を促進しないため、L1正則化を使用した場合に得られるような解釈性の高いモデルよりも解釈性が低い可能性があります。
Elastic Net正則化
Elastic Net正則化は、L1正則化とL2正則化の両方の利点を組み合わせたハイブリッド技術です。損失関数には、モデルの係数の絶対値と2乗が含まれます。Elastic Net正則化による変更された損失関数は、次のように表されます。
ここで、
Elastic Net正則化は、L1正則化のスパース性を促進する性質と、L2正則化の安定性を促進する性質をバランス良く組み合わせます。
メリット
-
L1正則化とL2正則化をバランス良く組み合わせている
Elastic Net正則化は、L1正則化のスパース性を促進する性質と、L2正則化の安定性を促進する性質をバランス良く組み合わせます。そのため、さまざまな問題に対して適した選択肢になります。 -
特徴量選択
Elastic Net正則化は、L1正則化と同様に特徴選択を実行できますが、多重共線性が存在する場合でもモデルの安定性を維持できます。
デメリット
-
計算コストが高い
Elastic Net正則化は、2つの正則化パラメータを最適化する必要があるため、L1正則化またはL2正則化よりも多くの計算リソースを必要とします。 -
ハイパーパラメータの調整が必要
追加のハイパーパラメータであるl1_ratio
適切な正則化技術の選択
適切な正則化技術の選択は、データセットのサイズ、多重共線性の存在、および所望のモデルの特性など、さまざまな要因に依存します。以下は、適切な正則化方法を選択するためのガイドラインです。
-
データセットのサイズ
データセットが小さい場合、L2正則化が一般的により適しています。これは、L1正則化よりも追加のバイアスが少ないためです。しかし、大きなデータセットの場合、L1正則化が有益である場合があります。なぜなら、スパース性を促進する性質により、より解釈可能なモデルが得られるからです。 -
多重共線性
データセットに多重共線性がある場合、L2またはElastic Net正則化がより適切である場合があります。これらは、相関する特徴の効果を分散させ、安定性を促進するためです。L1正則化は、相関する特徴のグループから1つの特徴だけを選択する傾向があるため、このような場合には適していません。 -
特徴量選択
特徴量選択を実行するモデルを望む場合、L1またはElastic Net正則化が適している場合があります。これらは、モデルの係数にスパース性を促進するため、特徴量選択を実行できます。L2正則化は、スパース性を促進しないため、特徴量選択を実行しません。 -
モデルの解釈性
モデルの解釈性を優先する場合、L1正則化が良い選択肢になることがあります。これは、L1正則化のスパース性によるものです。しかし、Elastic Net正則化は、多重共線性が存在する場合にもモデルの安定性を維持できるため、解釈可能なモデルを提供することができます。
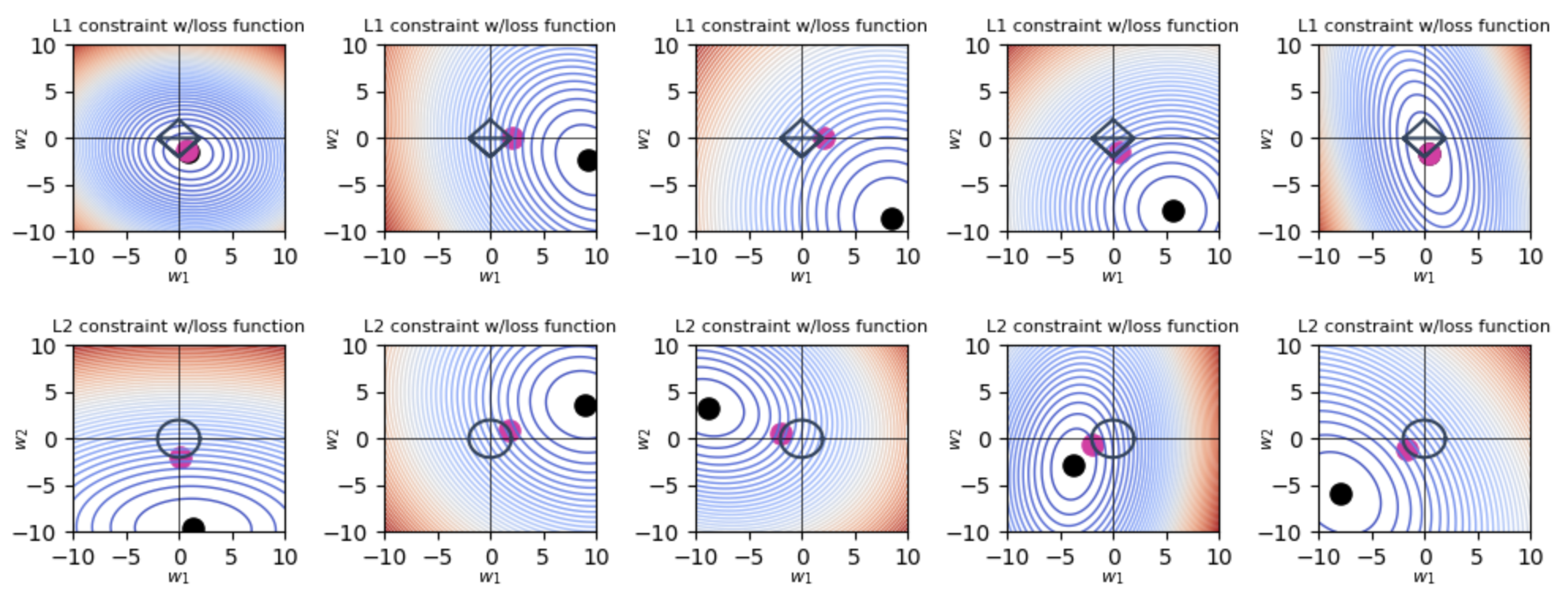
L1正則化とL2正則化の可視化
以下は、Pythonを使用してL1正則化とL2正則化をプロットするためのスクリプトです。
2Dプロット
import numpy as np
import matplotlib.pyplot as plt
import glob
import os
import warnings
lmbda = 2
w,h = 10,10
beta0 = np.linspace(-w, w, 100)
beta1 = np.linspace(-h, h, 100)
B0, B1 = np.meshgrid(beta0, beta1)
def diamond(lmbda=1, n=100):
"get points along diamond at distance lmbda from origin"
points = []
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, -x + lmbda)))
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, -x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, x + lmbda)))
return np.array(points)
def circle(lmbda=1, n=100):
points = []
for angle in np.linspace(0,np.pi/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi/2,np.pi, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi, np.pi*3/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi*3/2, 2*np.pi,num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
return np.array(points)
def loss(b0, b1,
a = 1,
b = 1,
c = 0,
cx = -10,
cy = 5):
return a * (b0 - cx) ** 2 + b * (b1 - cy) ** 2 + c * (b0 - cx) * (b1 - cy)
def select_parameters(lmbda, reg, force_symmetric_loss, force_one_nonpredictive):
while True:
a = np.random.random() * 10
b = np.random.random() * 10
c = np.random.random() * 4 - 1.5
if force_symmetric_loss:
b = a
c = 0
elif force_one_nonpredictive:
if np.random.random() > 0.5:
a = np.random.random() * 15 - 5
b = .1
else:
b = np.random.random() * 15 - 5
a = .1
c = 0
x, y = 0, 0
if reg=='L1':
while np.abs(x) + np.abs(y) <= lmbda:
x = np.random.random() * 2 * w - w
y = np.random.random() * 2 * h - h
else:
while np.sqrt(x**2 + y**2) <= lmbda:
x = np.random.random() * 2 * w - w
y = np.random.random() * 2 * h - h
Z = loss(B0, B1, a=a, b=b, c=c, cx=x, cy=y)
loss_at_min = loss(x, y, a=a, b=b, c=c, cx=x, cy=y)
if (Z >= loss_at_min).all():
break
return Z, a, b, c, x, y
def plot_loss(boundary, reg,
boundary_color='#2D435D',
boundary_dot_color='#E32CA6',
force_symmetric_loss=False, force_one_nonpredictive=False,
show_contours=True, contour_levels=50, show_loss_eqn=False,
show_min_loss=True,idx=None,fig=None,ax=None,num_trials=None):
Z, a, b, c, x, y = select_parameters(lmbda, reg,
force_symmetric_loss=force_symmetric_loss,
force_one_nonpredictive=force_one_nonpredictive)
eqn = f"{a:.2f}(b0 - {x:.2f})^2 + {b:.2f}(b1 - {y:.2f})^2 + {c:.2f} b0 b1"
n_col = 5
if show_loss_eqn:
ax[idx//n_col, idx%n_col].set_title(eqn, fontsize=10)
ax[idx//n_col, idx%n_col].set_xlabel("x", fontsize=8, labelpad=0)
ax[idx//n_col, idx%n_col].set_ylabel("y", fontsize=8, labelpad=-10)
ax[idx//n_col, idx%n_col].set_xticks([-10,-5,0,5,10])
ax[idx//n_col, idx%n_col].set_yticks([-10,-5,0,5,10])
ax[idx//n_col, idx%n_col].set_xlabel(r"$w_1$", fontsize=8)
ax[idx//n_col, idx%n_col].set_ylabel(r"$w_2$", fontsize=8)
shape = ""
if force_symmetric_loss:
shape = "symmetric "
elif force_one_nonpredictive:
shape = "orthogonal "
ax[idx//n_col, idx%n_col].set_title(f"{reg} constraint w/{shape}loss function", fontsize=8)
if show_contours:
ax[idx//n_col, idx%n_col].contour(B0, B1, Z, levels=contour_levels, linewidths=1.0, cmap='coolwarm')
else:
ax[idx//n_col, idx%n_col].contourf(B0, B1, Z, levels=contour_levels, cmap='coolwarm')
ax[idx//n_col, idx%n_col].plot([-w,+w],[0,0], '-', c='k', lw=.5)
ax[idx//n_col, idx%n_col].plot([0, 0],[-h,h], '-', c='k', lw=.5)
if boundary is not None:
ax[idx//n_col, idx%n_col].plot(boundary[:,0], boundary[:,1], '-', lw=1.5, c=boundary_color)
if show_min_loss:
ax[idx//n_col, idx%n_col].scatter([x],[y], s=90, c='k')
eqn = f"{a:.2f}(b0 - {x:.2f})^2 + {b:.2f}(b1 - {y:.2f})^2 + {c:.2f} (b0-{x:.2f}) (b1-{y:.2f})"
if boundary is not None:
losses = [loss(*edgeloc, a=a, b=b, c=c, cx=x, cy=y) for edgeloc in boundary]
minloss_idx = np.argmin(losses)
coeff = boundary[minloss_idx]
ax[idx//n_col, idx%n_col].scatter([coeff[0]], [coeff[1]], s=90, c=boundary_dot_color)
if force_symmetric_loss:
if reg=='L2':
ax[idx//n_col, idx%n_col].plot([x,0],[y,0], ':', c='k')
else:
ax[idx//n_col, idx%n_col].plot([x,coeff[0]],[y,coeff[1]], ':', c='k')
def plot_2d(reg, force_symmetric_loss=False, force_one_nonpredictive=False,num_trials=None):
if num_trials <=5:
fig,ax = plt.subplots(1,5,figsize=(10,2),squeeze=False)
elif num_trials > 5 and num_trials<=10:
fig,ax = plt.subplots(2,5,figsize=(10,4))
elif num_trials > 10 and num_trials<=15:
fig,ax = plt.subplots(3,5,figsize=(10,6))
fig.subplots_adjust(hspace=0.6, wspace=0.4)
if reg == 'L1':
boundary = diamond(lmbda=lmbda, n=100)
else:
boundary = circle(lmbda=lmbda, n=100)
for i in range(num_trials):
plot_loss(boundary=boundary, reg=reg,
force_symmetric_loss=force_symmetric_loss,
force_one_nonpredictive=force_one_nonpredictive,
contour_levels=contour_levels,idx=i,fig=fig,ax=ax,num_trials=num_trials)
shape_fname = ""
if force_symmetric_loss:
shape_fname = "symmetric-"
elif force_one_nonpredictive:
shape_fname = "orthogonal-"
plt.tight_layout()
if num_trials%5!=0:
k = 5*(1 + num_trials//5)-num_trials
for i in range(k):
fig.delaxes(ax[num_trials//5][-i-1])
plt.show()
n_trials = 5
contour_levels=50
s = 0
np.random.seed(s)
for mode in ["L1", "L2"]:
plot_2d(reg=mode,num_trials=n_trials)
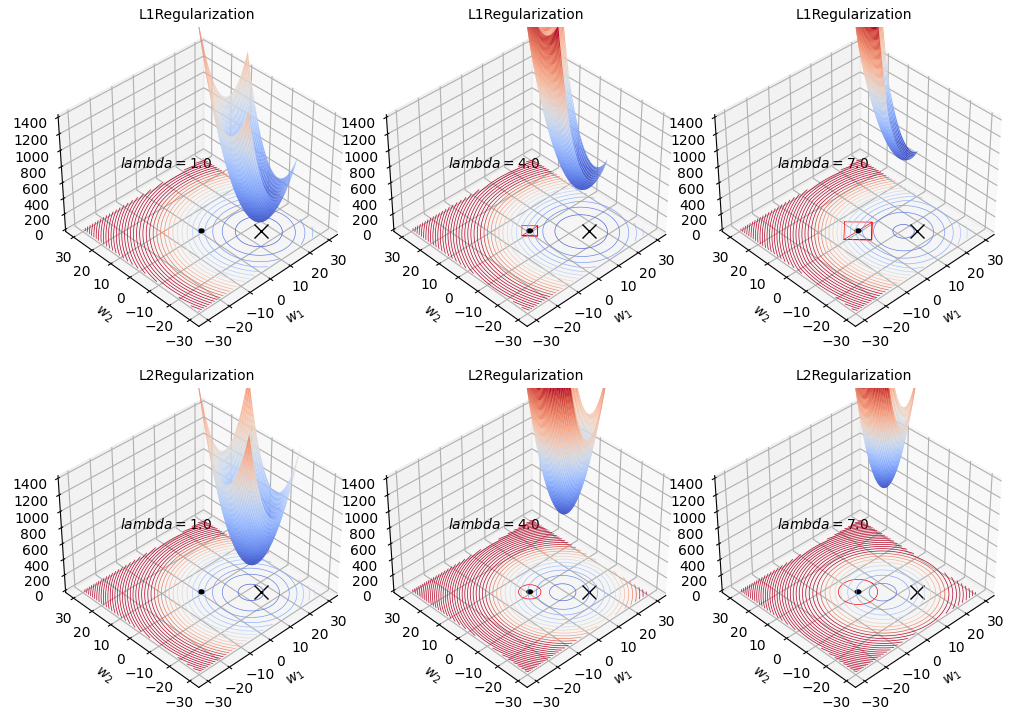
3Dプロット
# https://github.com/parrt/website-explained.ai/blob/master/regularization/code/l2loss_with_penalty.py
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import animation
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
from matplotlib.patches import Circle
import mpl_toolkits.mplot3d.art3d as art3d
import glob
import os
from PIL import Image as PIL_Image
def diamond(lmbda=1, n=100):
"get points along diamond at distance lmbda from origin"
points = []
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, -x + lmbda)))
x = np.linspace(0, lmbda, num=n // 4)
points.extend(list(zip(x, x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, -x - lmbda)))
x = np.linspace(-lmbda, 0, num=n // 4)
points.extend(list(zip(x, x + lmbda)))
return np.array(points)
def circle(lmbda=1, n=100):
points = []
for angle in np.linspace(0,np.pi/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi/2,np.pi, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi, np.pi*3/2, num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
for angle in np.linspace(np.pi*3/2, 2*np.pi,num=n//4):
x = np.cos(angle) * lmbda
y = np.sin(angle) * lmbda
points.append((x,y))
return np.array(points)
def loss(b0, b1,
a = 1,
b = 1,
c = 0, # axis stretch
cx = -10, # shift center x location
cy = 5, # shift center y
lmbda=1.0,
yintercept=100):
eqn = f"{a:.2f}(b0 - {cx:.2f})^2 + {b:.2f}(b1 - {cy:.2f})^2 + {c:.2f} (b0-{cx:.2f}) (b1-{cy:.2f}) + {yintercept}"
return lmbda * (a * (b0 - cx) ** 2 + b * (b1 - cy) ** 2) + c * (b0 - cx) * (b1 - cy) + yintercept
def loss_l1(b0,b1,a=1,b=1,c=0,cx=-10,cy=5,lmbda=1.0,yintercept=100):
return lmbda*(a*np.abs(b0-cx) + b*np.abs(b1-cy))
def plot_3d(mode, last_lmbda, stepsize, lmbdas):
fig = plt.figure(figsize=(10,10))
plt.subplots_adjust(wspace=0.4, hspace=2.0)
for i,lmbda in enumerate(lmbdas):
ax = fig.add_subplot(3,3,i+1, projection='3d')
ax.set_xlabel("$w_1$", labelpad=0)
ax.set_ylabel("$w_2$", labelpad=0)
ax.set_title(mode + "Regularization",fontsize=10)
ax.tick_params(axis='x', pad=0)
ax.tick_params(axis='y', pad=0)
ax.set_zlim(0, 1400)
cx = 15
cy = -15
ax.plot([cx], [cy], marker='x', markersize=10, color='black')
ax.text(-20,20,800, f"$lambda={lmbda:.1f}$", fontsize=10)
beta0 = np.linspace(-30, 30, 300)
beta1 = np.linspace(-30, 30, 300)
B0, B1 = np.meshgrid(beta0, beta1)
if mode=='L2':
Z1 = loss(B0, B1, a=1, b=1, c=0, cx=0, cy=0, lmbda=lmbda, yintercept=0)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
elif mode=='L1':
Z1 = loss_l1(B0,B1,a=5,b=5,cx=0,cy=0,lmbda=lmbda)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
origin = Circle(xy=(0, 0), radius=1, color='k')
ax.add_patch(origin)
art3d.pathpatch_2d_to_3d(origin, z=0, zdir="z")
scale = 1.5
vmax = 8000
contr = ax.contour(B0, B1, Z, levels=50, linewidths=.5,
cmap='coolwarm',
zdir='z', offset=0, vmax=vmax)
#surface plot
j = lmbda*scale
b0 = (j, 20-j)
beta0 = np.linspace(-j, 25-j, 300)
beta1 = np.linspace(-25+j, j, 300)
B0, B1 = np.meshgrid(beta0, beta1)
if mode=='L1':
Z1 = loss_l1(B0,B1,a=5,b=5,cx=0,cy=0,lmbda=lmbda)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
elif mode=='L2':
Z1 = loss(B0, B1, a=1, b=1, c=0, cx=0, cy=0, lmbda=lmbda, yintercept=0)
Z2 = loss(B0, B1, a=5, b=5, c=0, cx=cx, cy=cy, yintercept=0)
Z = Z1 + Z2
vmax = 2700
ax.plot_surface(B0, B1, Z, alpha=1.0, cmap='coolwarm', vmax=vmax)
if mode=="L1":
boundary = diamond(lmbda=lmbda)
ax.plot(boundary[:, 0], boundary[:, 1], '-', lw=.5, c="red")
elif mode=="L2":
boundary = circle(lmbda=lmbda)
ax.plot(boundary[:, 0], boundary[:, 1], '-', lw=.5, c="red")
ax.view_init(elev=38, azim=-134)
plt.tight_layout()
last_lmbda = 10
stepsize = 3.0
lmbdas = list(np.arange(1, last_lmbda, step=stepsize))
for mode in ["L1", "L2"]:
plot_3d(mode, last_lmbda, stepsize, lmbdas)
参考