多項式回帰とは
多項式回帰は、独立変数と従属変数の関係をn次元多項式関数としてモデル化する回帰分析の形式です。単純に言えば、変数間の複雑な非線形関係を捉えるための線形回帰の拡張であり、曲線的な傾向、振動、またはその他の複雑なパターンを持つデータをモデル化するための柔軟で強力なアプローチを提供します。
多項式回帰を使う理由
線形回帰モデルは解釈と実装が容易である一方、変数間の複雑な関係を捉える能力に制限があります。多くの現実世界では、入力と出力変数の関係は直線的ではなく、直線がデータの基礎となるパターンをもっともよく表現するとは限りません。
多項式回帰を使うことで、データに対して曲線をフィットさせ、変数間の幅広い関係をモデル化することができます。多項式回帰を使うことの主な利点は次のとおりです。
-
柔軟性
多項式の次数を調整することで、モデルの複雑さを制御し、データのさまざまなパターンを捉えることができます。 -
解釈性
多項式回帰モデルは、線形モデルよりは複雑ですが、比較的解釈しやすく理解しやすいです。 -
適用範囲
多項式回帰は、住宅価格の予測から感染症の拡散のモデル化に至るまで、幅広い問題に適用することができます。
多項式回帰の数学的背景
線形回帰
線形回帰は、独立変数
多項式関数
多項式関数とは、変数と係数だけで構成され、加算、減算、乗算、非負整数の指数演算だけで表現される数学的式です。次数
ここで、
多項式回帰モデル
多項式回帰では、多項式関数をデータにフィットさせることで、線形回帰モデルを拡張します。次数
多項式回帰の目的は、最適な係数
係数の決定: 最小二乗法
最小二乗法は、多項式回帰モデルの最適な係数を見つけるために使用される最適化技術です。目的は、残差平方和(RSS)を最小限に抑えるように、予測値と観測値の差(残差)の2乗和を最小化することです。
最小二乗法を用いて、各係数についてRSS関数の偏微分を行い、それらをゼロに設定します。この連立方程式を解くことで、最適な係数
Pythonでの多項式回帰の実装
この章では、Pythonを使って多項式回帰を実装する方法について、人気のあるmpgデータセットに焦点を当てて説明します。
まず、必要なライブラリをインポートし、mpgデータセットを読み込みます。データセットはseabornライブラリで利用可能です。
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score
# Load the mpg dataset
mpg = sns.load_dataset("mpg")
# Display the first five rows
print(mpg.head())
mpg cylinders displacement horsepower weight acceleration \
0 18.0 8 307.0 130.0 3504 12.0
1 15.0 8 350.0 165.0 3693 11.5
2 18.0 8 318.0 150.0 3436 11.0
3 16.0 8 304.0 150.0 3433 12.0
4 17.0 8 302.0 140.0 3449 10.5
model_year origin name
0 70 usa chevrolet chevelle malibu
1 70 usa buick skylark 320
2 70 usa plymouth satellite
3 70 usa amc rebel sst
4 70 usa ford torino
この例では、独立変数(x)としてhorsepowerを、従属変数(y)としてmpgを使用します。また、欠損値のある行は削除します。
# Remove missing values and select the relevant columns
mpg_cleaned = mpg[['horsepower', 'mpg']].dropna()
# Separate the features and the target variable
X = mpg_cleaned['horsepower'].values.reshape(-1, 1)
y = mpg_cleaned['mpg'].values
次に、独立変数horsepowerの多項式特徴量を作成します。この例では、2次の多項式を使用します。
# Create polynomial features
poly_features = PolynomialFeatures(degree=2)
X_poly = poly_features.fit_transform(X)
データをトレーニングセットとテストセットに分割し、多項式回帰モデルをトレーニングし、平均二乗誤差(MSE)とR2を使用してその性能を評価します。
# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X_poly, y, test_size=0.2, random_state=42)
# Train the polynomial regression model
poly_reg = LinearRegression()
poly_reg.fit(X_train, y_train)
# Make predictions and evaluate the model
y_pred = poly_reg.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)
print("Mean Squared Error: ", round(mse, 2))
print("R-squared: ", round(r2, 2))
Mean Squared Error: 18.42
R-squared: 0.64
最後に、matplotlibとseabornを使用して多項式回帰を可視化します。
# Set seaborn style
sns.set(style="whitegrid")
# Create a scatterplot of the data
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label="Data points")
# Plot the polynomial regression curve
X_plot = np.linspace(X.min(), X.max(), 100).reshape(-1, 1)
X_plot_poly = poly_features.transform(X_plot)
y_plot = poly_reg.predict(X_plot_poly)
plt.plot(X_plot, y_plot, color='red', linewidth=2, label="Polynomial Regression")
# Customize the plot appearance
plt.xlabel("Horsepower")
plt.ylabel("Miles per Gallon (mpg)")
plt.title("Polynomial Regression of Degree 2: Horsepower vs. MPG")
plt.legend()
plt.show()
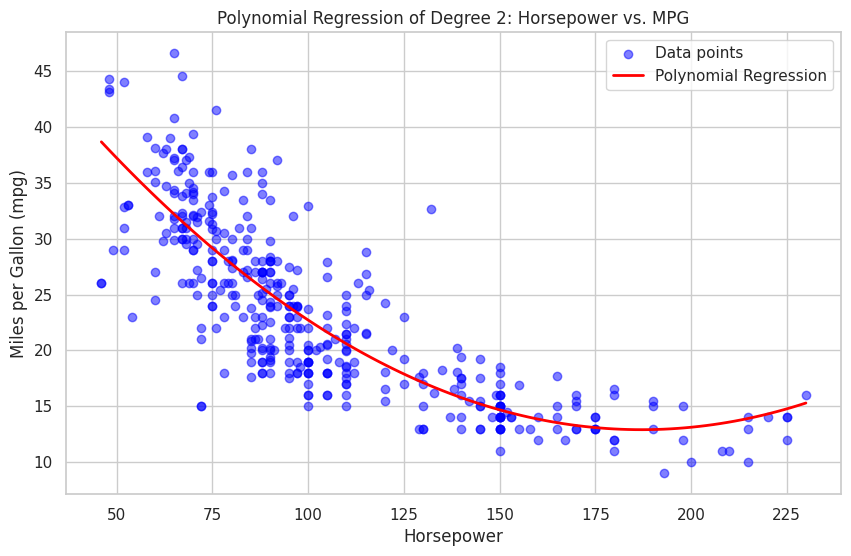
生成されたプロットは多項式回帰を表示し、horsepowerとmpgの関係を示しています。多項式の次数や、データセット内の他の特徴量を試して、モデルの性能や可視化の変化を探索することができます。
参考