2022-11-24

サポートベクター回帰

Machine Learning

Regression

Python

sklearn

サポートベクター回帰（SVR）とは

サポートベクター回帰（SVR）は、分類のためのよく知られたサポートベクターマシン（SVM）から派生した強力で多目的な機械学習アルゴリズムであり、一連の入力特徴量が与えられた場合に、連続的な目的変数を予測することを目的としています。

SVRの主要な概念

SVRは、入力特徴量と目的変数の関係を近似する関数を見つけることを目指し、特定の許容誤差範囲内で予測エラーを最小化することが目的です。SVRの主要な概念には以下があります。

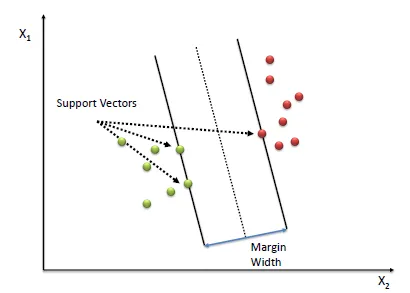
サポートベクター
これらは、近似関数の周囲にあるまたは外側にあるデータポイントです。サポートベクターは、最適なパラメータを決定するために重要な役割を果たします。

Machine Learning: Support Vector Regression (SVR)

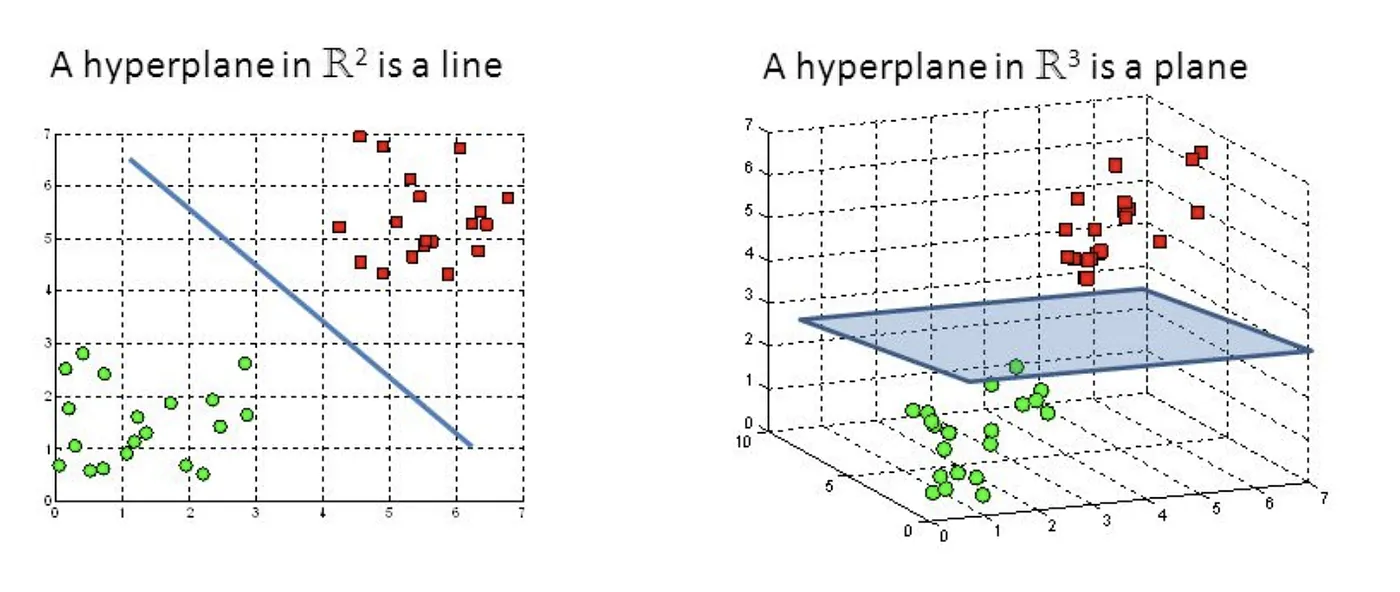
ハイパープレーン
ハイパープレーンは、環境空間よりも1次元少ない平面部分空間です。SVRの文脈では、ハイパープレーンは入力特徴量と目的変数の関係を近似するために使用されます。線形SVRの場合、ハイパープレーンは線形関数を表し、非線形SVRの場合、カーネル変換を用いて取得した高次元空間に存在します。

Hyperplane
Machine Learning: Support Vector Regression (SVR)

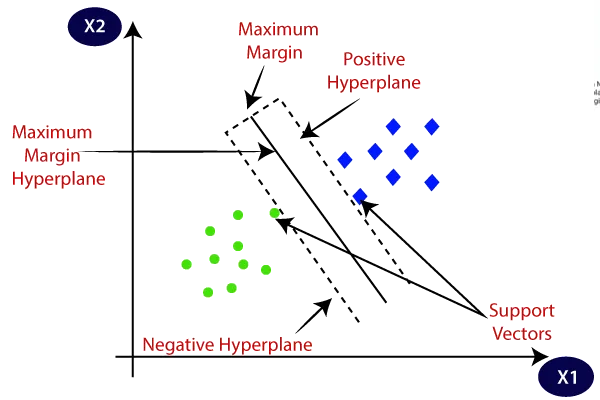
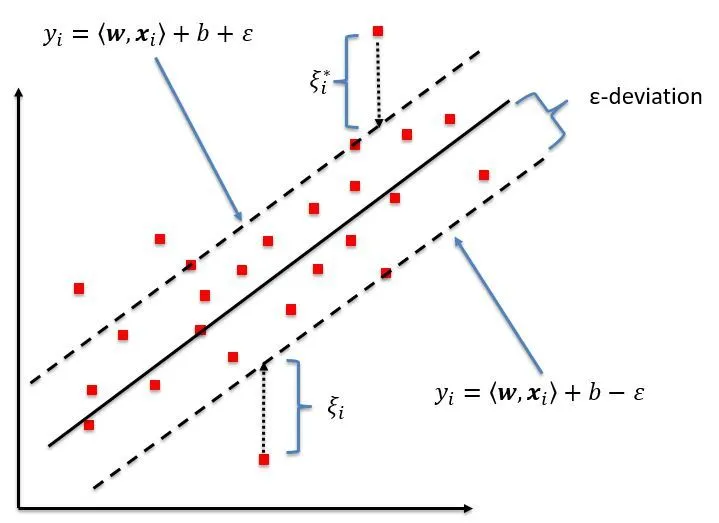
マージン
マージンは、近似関数（ハイパープレーン）の周囲の許容範囲であり、エラーが許容される範囲です。SVRは、指定された許容範囲内で予測エラーを最小化しながら、マージンを最大化することを目的としています。マージンの幅は、パラメータ $\epsilon$ によって決定されます。

Margin
Machine Learning: Support Vector Regression (SVR)

SVR
Machine Learning: Support Vector Regression (SVR)

カーネルトリック
カーネルトリックは、非線形SVRで使用されるテクニックで、予測エラーを指定された許容誤差範囲内に保ちつつ、入力特徴量と目的変数の非線形関係をもっとも近似する非線形関数を見つけるために使用されます。カーネルトリックは、カーネル関数を使用して入力データを高次元空間にマッピングし、線形関数を使用して非線形関係を近似する方法です。これにより、SVRは入力データを明示的に変換せずに非線形問題を解決でき、計算複雑性を低減することができます。

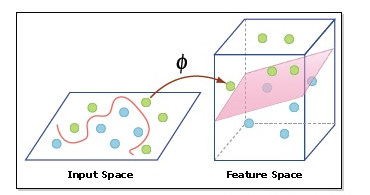
kernel
Support Vector Regression Tutorial for Machine Learning

SVRの数学的基礎

線形回帰とSVR

線形回帰では、予測値と実測値の二乗誤差を最小化することで最適なフィッティングラインを見つけようとします。線形関数は次のように与えられます。

f(x) = w^T x + b

ここで、 $w$ は重みベクトル、 $x$ は入力特徴量ベクトル、 $b$ はバイアス項です。一方、SVRは、真の目的変数の周囲に指定されたマージン（許容範囲）内にある関数を見つけることに焦点を当てています。

最適化問題

SVRは、次の最適化問題を解くことにより、最適な重みベクトル $w$ とバイアス項 $b$ を見つけようとします。

目的関数

\min_{w, b} \frac{1}{2} ||w||^2 + C \sum_{i=1}^N (\xi_i + \xi_i^*)

ここで、 $||w||^2$ は重みベクトル $w$ の二乗ノルム、 $C$ は正則化パラメータ、 $N$ はデータポイントの数、 $\xi_i$ と $\xi_i^*$ は予測値と真の目標値の偏差を測定するスラック変数です。

制約条件

最適化問題の制約条件は、次のように定義されます。

\begin{aligned} y_i - f(x_i) &\leq \epsilon + \xi_i \\ f(x_i) - y_i &\leq \epsilon + \xi_i^* \\ \xi_i, \xi_i^* &\geq 0, \quad i = 1, \dots, N \end{aligned}

ここで、 $y_i$ は $i$ 番目のデータポイントの真の目的変数であり、 $\epsilon$ は許容マージンです。

損失関数

SVRは、指定されたマージン $\epsilon$ 内にあるエラーをペナルティとせず、 $\epsilon$ -insensitive損失関数を使用します。

L_\epsilon(y, f(x)) = \max(0, |y - f(x)| - \epsilon)

$\epsilon$ -insensitive損失関数は、指定されたマージン $\epsilon$ 内にあるエラーをペナルティとせず、許容されます。

双対形式

SVR問題の双対形式は、ラグランジュ関数にKarush-Kuhn-Tucker（KKT）条件を適用することで得られます。この再定式化により、最適化問題をより効率的に解くことができ、非線形カーネルを組み込むことができます。

ラグランジュ乗数

双対問題を導出するために、最適化問題の各制約に対してラグランジュ乗数 $\alpha_i, \alpha_i^* \geq 0$ を導入します。ラグランジュ関数は次のように定義されます。

\mathcal{L}(w, b, \xi, \xi^*, \alpha, \alpha^*) = \frac{1}{2} ||w||^2 + C \sum_{i=1}^N (\xi_i + \xi_i^*) - \sum_{i=1}^N (\alpha_i - \alpha_i^*)(y_i - w^T x_i - b - \epsilon - \xi_i) - \sum_{i=1}^N (\alpha_i + \alpha_i^*)(\xi_i + \xi_i^*)

Karush-Kuhn-Tucker（KKT）条件

ラグランジュ関数にKKT条件を適用することで、ラグランジュ乗数 $\alpha$ と $\alpha^*$ に関して次の双対目的関数を最大化する双対問題を導出します。

\max_{\alpha, \alpha^*} \Bigg( -\frac{1}{2} \sum_{i=1}^N \sum_{j=1}^N (\alpha_i - \alpha_i^*)(\alpha_j - \alpha_j^*) y_i y_j x_i^T x_j + \sum_{i=1}^N (\alpha_i + \alpha_i^*) y_i - \epsilon \sum_{i=1}^N (\alpha_i + \alpha_i^*) \Bigg)

次の制約条件に従います。

\begin{aligned} \sum_{i=1}^N (\alpha_i - \alpha_i^*) &= 0 \\ \alpha_i, \alpha_i^* &\in[0, C], \quad i = 1, \dots, N \end{aligned}

双対形式により、非線形カーネルを使用する場合、内積 $x_i^T x_j$ をカーネル関数 $K(x_i, x_j)$ に置き換えることで、入力データを明示的に変換することなく、非線形関係を処理できます。

カーネルトリック

カーネル関数

非線形SVRでは、入力データを高次元空間にマッピングするためにカーネルトリックを使用し、線形関数を使用して非線形関係を近似します。カーネル関数は、変換された空間での2つの入力特徴量ベクトルの内積を計算する類似性尺度です。

K(x_i, x_j) = \phi(x_i)^T \phi(x_j)

ここで、 $\phi(x_i)$ と $\phi(x_j)$ は入力特徴量ベクトル $x_i$ と $x_j$ のマッピングを示します。

SVRで使用される人気のあるカーネル

SVRで使用される一部の人気のあるカーネル関数には、以下があります。

線形カーネル

K(x_i, x_j) = x_i^T x_j

多項式カーネル

K(x_i, x_j) = (x_i^T x_j + c)^d

径基底関数（RBF）カーネル

K(x_i, x_j) = \exp(-\gamma ||x_i - x_j||^2)

シグモイドカーネル

K(x_i, x_j) = \tanh(\kappa x_i^T x_j + c)

双対目的関数で内積 $x_i^T x_j$ をカーネル関数 $K(x_i, x_j)$ に置き換えることにより、非線形SVRの双対問題が得られます。

PythonでのSVRの実装

この章では、Pythonとscikit-learnライブラリを使用してSVRを実装します。アヤメのデータセットを使用し、様々なカーネル関数に対するサポートベクターを可視化します。

まず、アヤメのデータセットをロードし、回帰に必要な形式に変換します。

python

from sklearn import datasets
from sklearn.model_selection import train_test_split

iris = datasets.load_iris()
X = iris.data[:, :2]  # Use the first two features.
y = iris.data[:, 2]   # Use the third feature as the target.

# Split the dataset into a training set and a test set.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

次に、様々なカーネル関数を使用して、SVRモデルをトレーニングします。

python

from sklearn.svm import SVR

# Initialize SVR models with different kernels.
svr_linear = SVR(kernel='linear', C=1)
svr_poly = SVR(kernel='poly', C=1, degree=3)
svr_rbf = SVR(kernel='rbf', C=1, gamma='auto')

# Train the SVR models.
svr_linear.fit(X_train, y_train)
svr_poly.fit(X_train, y_train)
svr_rbf.fit(X_train, y_train)

サポートベクターを可視化するために、データポイントの散布図を作成し、サポートベクターを強調します。

python

import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np

sns.set(style="darkgrid")

def plot_support_vectors(svr_model, X, y, title, ax):
    h = .02  # step size in the mesh
    # Create a mesh to plot in.
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
                         np.arange(y_min, y_max, h))

    # Predict target values for the mesh.
    Z = svr_model.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    # Plot the contour of the predictions.
    ax.contourf(xx, yy, Z, alpha=0.8)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=50)
    ax.set_title(title)
    ax.legend(*scatter.legend_elements())

fig, axes = plt.subplots(1, 3, figsize=(18, 6))
plot_support_vectors(svr_linear, X_train, y_train, 'SVR with Linear Kernel', axes[0])
plot_support_vectors(svr_poly, X_train, y_train, 'SVR with Polynomial Kernel', axes[1])
plot_support_vectors(svr_rbf, X_train, y_train, 'SVR with RBF Kernel', axes[2])

plt.show()

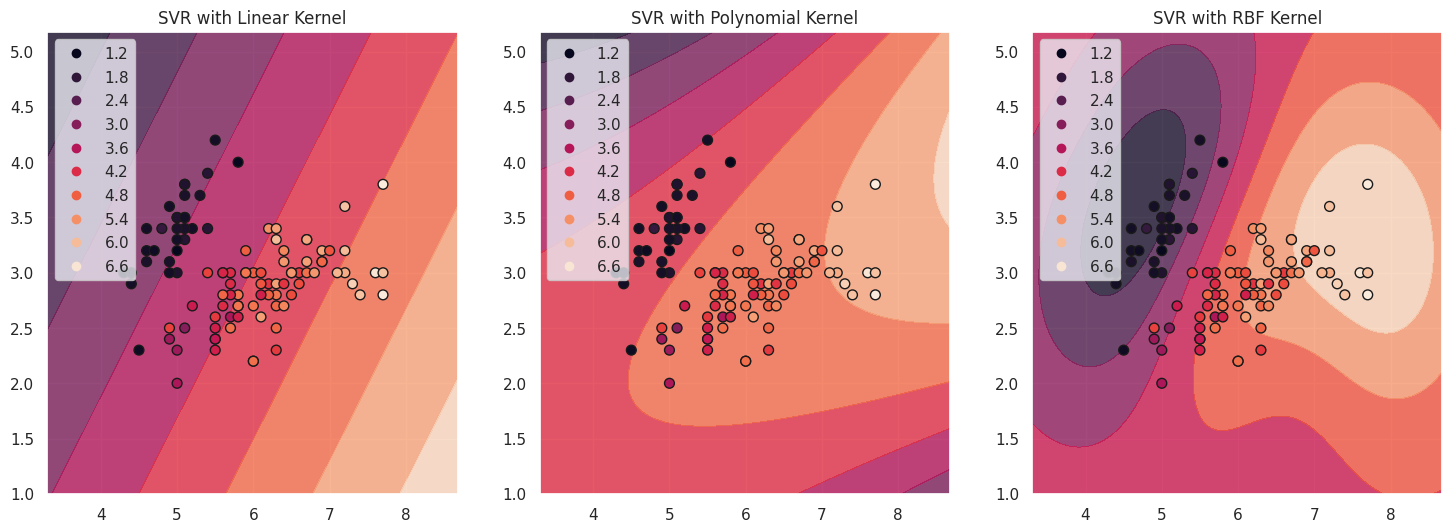
SVR with various kernel function

サポートベクターとは、マージンの内側または境界線上にあるデータポイントのことです。これらはハイパープレーンの位置を決定する上で重要であり、モデルの予測に大きな影響を与えます。上のプロットでは、サポートベクターはそれぞれのカーネル関数の近似関数の等高線上の点で表されます。これらの点は、決定境界の形状やSVRモデルの全体的なパフォーマンスを決定する上で重要な役割を果たします。

異なるカーネルを使用したSVRモデルのパフォーマンスを評価するために、テストセットでの平均二乗誤差（MSE）とR-squaredスコアを計算することができます。

python

from sklearn.metrics import mean_squared_error, r2_score

def evaluate_model(svr_model, X_test, y_test):
    y_pred = svr_model.predict(X_test)
    mse = mean_squared_error(y_test, y_pred)
    r2 = r2_score(y_test, y_pred)
    return mse, r2

mse_linear, r2_linear = evaluate_model(svr_linear, X_test, y_test)
mse_poly, r2_poly = evaluate_model(svr_poly, X_test, y_test)
mse_rbf, r2_rbf = evaluate_model(svr_rbf, X_test, y_test)

print("Linear kernel: MSE = {:.2f}, R^2 = {:.2f}".format(mse_linear, r2_linear))
print("Polynomial kernel: MSE = {:.2f}, R^2 = {:.2f}".format(mse_poly, r2_poly))
print("RBF kernel: MSE = {:.2f}, R^2 = {:.2f}".format(mse_rbf, r2_rbf))

Linear kernel: MSE = 0.31, R^2 = 0.91
Polynomial kernel: MSE = 0.54, R^2 = 0.84
RBF kernel: MSE = 0.30, R^2 = 0.91

これにより、各SVRモデルの平均二乗誤差とR-squaredスコアが出力されます。これらのメトリックを比較することで、データに最適なカーネルを決定することができます。

参考

多項式回帰

回帰問題の評価指標

Descriptive Statistics

Differential Equation

Dimensionality Reduction

Discrete Choice Model

Google Search Console

Hugging Face

Hypothesis Testing

Inferential Statistics

Probability Distribution

Ryusei Kakujo

Focusing on data science for mobility

Bench Press 100kg!