勾配ブースティング決定木(GBDT)とは
勾配ブースティング決定木(GBDT)は、決定木と勾配ブースティングの強みを組み合わせた強力なアンサンブル学習です。複雑な問題を扱う高性能なモデルを提供できるため、近年、金融、医療、マーケティングなどのさまざまな領域で人気が高まっています。
GBDTは、各ツリーが直前のツリーで行った誤りを修正しようとする一連の決定木を反復的に構築することで機能します。このプロセスは、指定されたツリー数が作成されるか、あるいはあらかじめ定義された性能レベルに達するまで続けられます。複数のツリーの予測を組み合わせることで、GBDTは単一の決定木よりも高い精度と汎化性能を実現することができます。
GBDTのアルゴリズム
このセクションでは、回帰および分類の両方の場合に焦点を当て、GBDTアルゴリズムについて説明します。GBDTの主なアイデアは、各ツリーが前のツリーで行った誤りを修正するように訓練された一連の弱い決定木を構築することです。モデルを反復的に改善することで、GBDTは高い精度と汎化性能を実現できます。GBDTアルゴリズムの主要な構成要素について説明します。
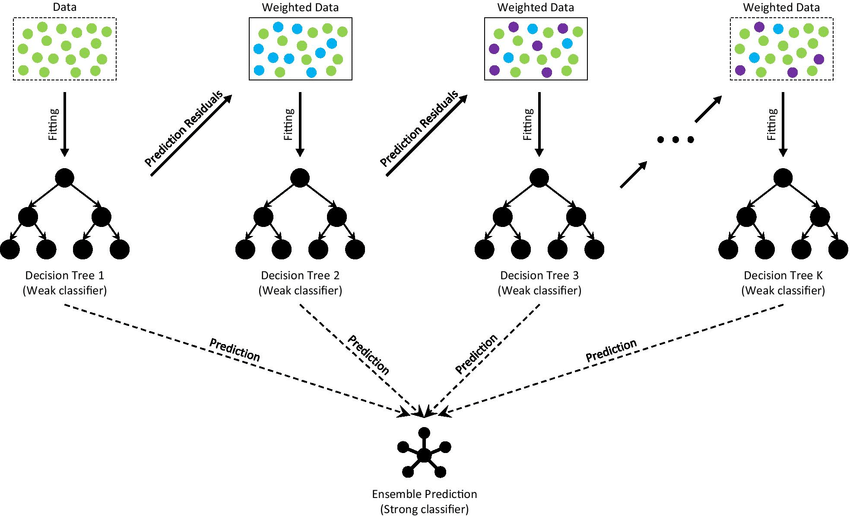
The architecture of Gradient Boosting Decision Tree
- 一定の予測値でモデルを初期化
GBDTは、一定の予測値でモデルを初期化して開始します。回帰問題では、この定数は通常、目標値の平均値であり、分類問題では、大多数のクラスの対数オッズであることがあります。
回帰問題では、初期予測
二値分類の場合、初期予測
ここで、
- 決定木を反復的に構築
GBDTは、損失関数の擬似残差(勾配)に新しいツリーを適合させることで、一連の決定木を構築します。擬似残差は、現在のモデルの予測に関する損失関数の負の勾配として計算されます。これにより、損失を最小化してターゲット関数の近似度合いを改善することができます。
最小二乗損失関数を使用した回帰の場合、反復
ロジスティック損失関数を使用した二値分類の場合、反復
- 加重決定木予測でモデルを更新
新しい決定木
- プロセスを停止
アルゴリズムは、あらかじめ定義されたツリー数に達するか、性能の改善が無視できるようになるまで、決定木を構築して追加し続けます。
GBDT vs. ランダムフォレスト
GBDTとランダムフォレストは、どちらも決定木をベースラーナーとして使用するアンサンブル方法ですが、次のような主な違いがあります。
-
ブースティング vs. バギング
GBDTはブースティングアルゴリズムであり、各ツリーは直前のツリーの誤りを修正するために順次構築されます。一方、ランダムフォレストはバギングアルゴリズムであり、データセットのブートストラップサンプルを使用して独立してツリーを構築します。 -
ツリー構造
GBDTは通常、弱い学習者である浅いツリーを使用し、一方、ランダムフォレストは深く完全に成長したツリーを使用します。 -
モデルの複雑さ
ブースティングの反復的な性質により、GBDTモデルはランダムフォレストよりも複雑になる可能性があります。これにより、性能が向上する一方で、過学習のリスクが高まる可能性があります。 -
トレーニング速度
GBDTモデルのトレーニングは、ツリーを順次構築する必要があるため、ランダムフォレストのトレーニングよりも遅くなる場合があります。ただし、GBDTモデルは、より少ないツリーで同等またはより良い性能を実現できるため、トレーニング時間の増加を相殺することができます。 -
解釈性
GBDTとランダムフォレストのモデルは、単一の決定木よりも解釈性が低くなりますが、GBDTの場合は、ツリーの順次構築と勾配情報の使用により、さらに解釈が難しくなる場合があります。 -
ノイズデータへの堅牢性
ランダムフォレストは、複数の独立したツリーを構築し、その予測を平均化するため、一般的にノイズデータに対してより堅牢です。一方、GBDTは、各ツリーが直前のツリーの誤りに影響を受けるため、ノイズに対してより敏感である場合があります。 -
ハイパーパラメータのチューニング
GBDTは、学習率や正則化などの追加のパラメータを含むため、ランダムフォレストよりも多くのハイパーパラメータの調整が必要になる場合があります。
PythonでGBDTを実装
以下は、GBDTモデルの実装に使用されるPythonスクリプトです。回帰用にはCalifornia Housingデータセット、分類用にはIrisデータセットを使用しています。
回帰: California Housingデータセット
import numpy as np
import pandas as pd
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error
data = fetch_california_housing()
X, y = data.data, data.target
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Create and train the GBDT model
gbdt_regressor = GradientBoostingRegressor(
n_estimators=100,
max_depth=3,
learning_rate=0.1,
random_state=42
)
gbdt_regressor.fit(X_train, y_train)
# Evaluate the model
y_pred = gbdt_regressor.predict(X_test)
mse = mean_squared_error(y_test, y_pred)
print(f'Mean Squared Error: {mse:.4f}')
Mean Squared Error: 0.2940
分類: Irisデータセット
from sklearn.datasets import load_iris
data = load_iris()
X, y = data.data, data.target
# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.metrics import accuracy_score
# Create and train the GBDT model
gbdt_classifier = GradientBoostingClassifier(
n_estimators=100,
max_depth=3,
learning_rate=0.1,
random_state=42
)
gbdt_classifier.fit(X_train, y_train)
# Evaluate the model
y_pred = gbdt_classifier.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy: {accuracy:.4f}')
Accuracy: 1.0000
参考