2022-11-04

最適化アルゴリズム

最適化アルゴリズムとは

ニューラルネットワークの学習の目的は、損失関数の値をできるだけ小さくするパラメータを見つけることです。最適化アルゴリズムとは、この損失の最小値に効率よくたどり着くためのアルゴリズムです。

最適化アルゴリズムは、よく冒険家に例えられます。地図を見ずに目隠ししながら広大な土地のもっとも深い谷底を目指すというものです。目隠ししているため谷底を目指すには足元の傾斜のみが頼りです。足元の傾斜を感じ取って谷底を目指す戦略を考えることになります。戦略を誤ると局所的に凹んだ場所にたどり着いてしまったり、谷底にたどり着くまでに遠回りしてしまいます。いかに効率的に、かつ正しい最小値にたどり着くかが重要になります。

勾配降下法

勾配降下法とは、パラメータで損失関数を微分し、損失を小さくする方向を探索してその方向にパラメータを調整させていく方法です。勾配降下法では次のステップを繰り返します。

ニューラルネットワークにデータを入力して予測値を出力
正解値と予測値の損失関数を定義
損失関数をパラメータで微分
微分して得られた値でパラメータ更新

このステップを数式で表すと次のようになります。

w_{t+1} = w_t-\eta\frac{\partial L}{\partial w_t}

ここで、 $w$ は更新 $t$ 回目のパラメータ、 $L$ は損失関数、 $\frac{\partial L}{\partial w}$ を $w$ に関する損失関数の勾配、 $\eta$ は学習率（learning rate）というハイパーパラメータを表しています。パラメータを更新するための式は更新式と呼ばれます。

パラメータ更新には次の2点を決める必要があります。

パラメータの値を増やすか減らすか
パラメータの値をどれだけ変化させるか

一つ目のパラメータの値の増減は、微分による傾きにより決定します。二つ目のパラメータの値の変化量は学習率により決定します。

勾配降下法は利用するデータの量によって次の3種類に分けられます。

最急降下法（バッチ勾配降下法）
SGD（確率的勾配降下法）
ミニバッチSGD

最急降下法（バッチ勾配降下法）

最急降下法は全データを使って損失関数の最小値を探索します。つまり全てのデータの平均のデータに対して勾配降下法を使うことになります。

最急降下法は一気にパラメータを更新することができる一方、次のデメリットがあります。

計算量が多くなる
局所最適解に陥ったときに抜け出せない

デメリットのうち、計算量が多くなることについては、並列計算で解決することができます。しかし、局所最適解に陥ったときに抜け出せないという点はどうしても避けられません。局所最適解というのは、最小値でない極小値です。毎回のパラメータ更新で同じデータを使っていると、に全く同じデータを入れているだけなので一回極小値に陥った場合に抜け出せません。この問題を解決するのがSGDになります。

SGD（確率的勾配降下法）

SGD（Stochastic gradient descent）はパラメータの更新毎にランダムにデータを選び出すアルゴリズムです。最急降下法では一回のパラメータ更新に全データを使用しますが、SGDは一回の更新ではランダムにピックアップした1つのデータしか使いません。そのため、SGDは、最急降下法で起こりうる局所最適解への収束という問題点を、 $w$ の更新ごとにランダムにサンプルを選び出すことで解消することができます。また、訓練データにおける冗長性を効率良く学習することができるという利点もあります。

SGDのデメリットとしては、1つのデータによる勾配で更新しないと次のデータには移れないため、並列化ができず、学習が遅くなってしまう点があります。

ミニバッチ SGD

ミニバッチSGDは、SGDと最急降下法の間をとった方法になります。データの一部を利用して損失関数の最小値を探索します。

最急降下法では、全データの勾配を計算するためその計算を並列化することができます。一方でSGDは勾配計算のデータ数が1つでありるため計算の並列化ができません。そこで、一定数のデータを使って学習するミニバッチSGDにより、ランダム性を保ちつつ並列化を実現することができます。つまりミニバッチSGDは、最急降下法とSGDの間をとった方法になります。ミニバッチSGDのバッチサイズはハイパーパラメータであり、16や32などがよく採用されます。

しかし、ミニバッチSGDを利用しても損失関数の最小値を探索するときにPathological Curvatureというくぼみにハマってしまい、オーバーシュート（一度の更新が大きすぎると起きる振動）を起こし、学習に時間がかかってしまうという問題点があります。この振動の問題を説明するために、次の関数の最小値を求める問題を考えます。

f(x,y) = \frac{1}{20}x^2 + y^2

この関数は $x$ 軸方向に伸びた楕円の形状をしています。この関数の勾配は $x$ 軸方向は小さく、 $y$ 軸方向は大きいのが特徴です。この関数の最小値は $(x, y) = (0,0)$ です。探索を $(x, y) = (-7,2)$ からスタートし、SGDを適用します。コードは以下になります。

import numpy as np
import matplotlib.pyplot as plt

class SGD:
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]


def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0

optimizer = SGD(lr=0.95)

x_history = []
y_history = []
params['x'], params['y'] = init_pos[0], init_pos[1]

for i in range(30):
    x_history.append(params['x'])
    y_history.append(params['y'])

    grads['x'], grads['y'] = df(params['x'], params['y'])
    optimizer.update(params, grads)

x = np.arange(-10, 10, 0.01)
y = np.arange(-5, 5, 0.01)

X, Y = np.meshgrid(x, y)
Z = f(X, Y)

# for simple contour line
mask = Z > 7
Z[mask] = 0

# plot
plt.figure(figsize=(12,6))
plt.plot(x_history, y_history, 'o-', color="red")
plt.contour(X, Y, Z)
plt.ylim(-10, 10)
plt.xlim(-10, 10)
plt.plot(0, 0, '+')
plt.title("SGD")
plt.xlabel("x")
plt.ylabel("y")

plt.show()

SGD

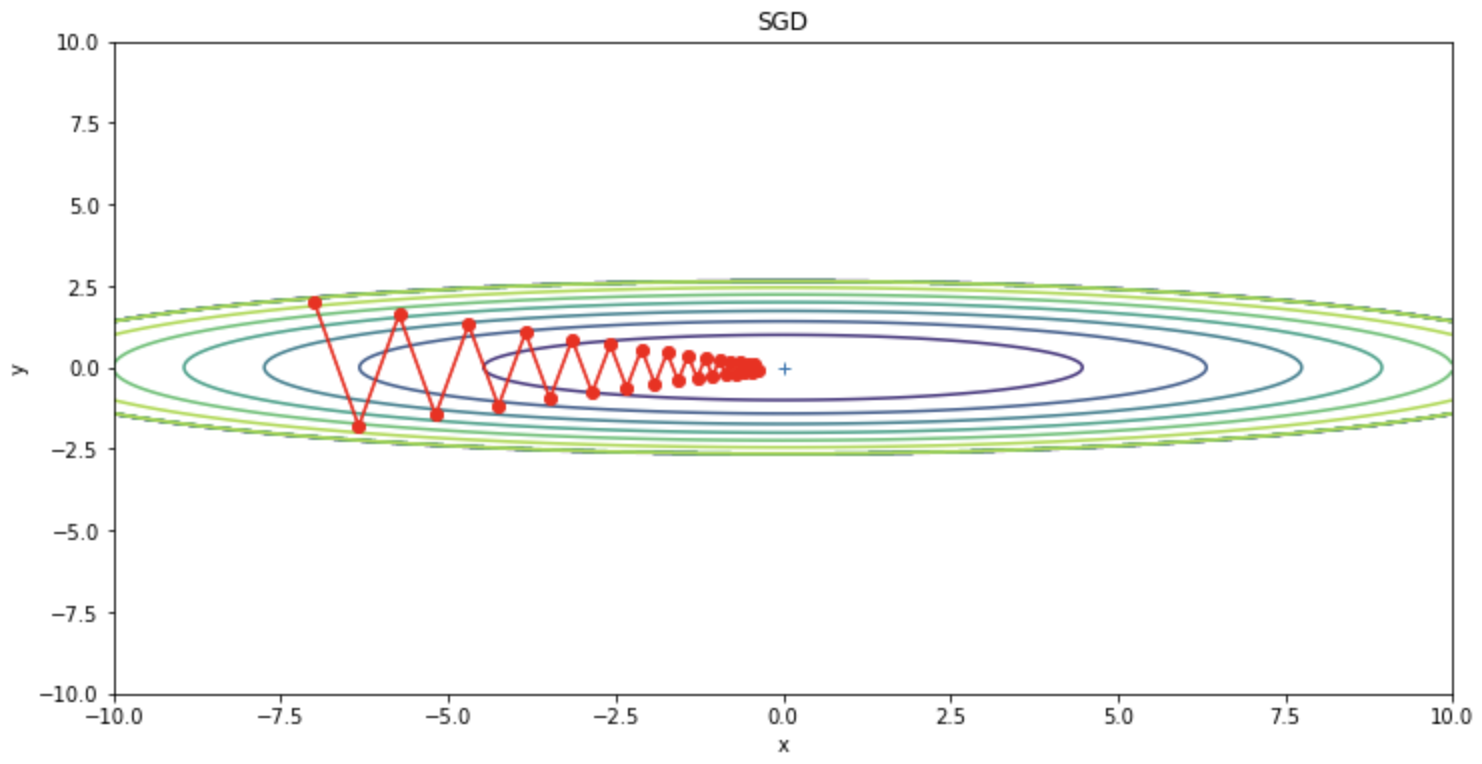
SGDはジグサグと振動していることが確認できます。この振動は非効率な経路であり、学習を遅くする要因となっています。このように、関数の形状が等方的でない場合はSGDはジグザグと非効率な経路で探索してしまいます。

この振動を抑えるために、Momentum、AdaGradおよびAdaGradを改良したRMSPropが派生しました。Momentumは微分の観点、AdaGradとRMSPropは学習率の観点から、過去の勾配の変化を用いてSDGの振動を抑えます。

Momentum

Momentumは、SGDにモーメンタム（慣性項）を付け加えたアルゴリズムです。モーメンタムは勾配の移動平均になります。移動平均の緩やかな変化になるという性質を利用することでSGDの振動を抑えることができます。Momentumは次の更新式で表されます。

v_{t+1} = \beta v_t + (1- \beta)\frac{\partial L}{\partial w_t}

w_{t+1} = w_t - \eta v_{t+1}

ここで、 $v_{t+1}$ はモーメンタム（つまりは勾配の移動平均）であり、 $\beta$ はモーメンタムの強さを決めるハイパーパラメータです。 $v_{t+1}$ により、新たな更新量はこれまでの更新量の影響を受けるようになり、振動を抑えてより滑らかな更新が実現されます。Momentumを使ってSGDと同様に $f(x,y) = \frac{1}{20}x^2 + y^2$ の最小値を探索します。Momentumの実装コードは以下になります。

class Momentum:
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]

optimizer = Momentum(lr=0.1)

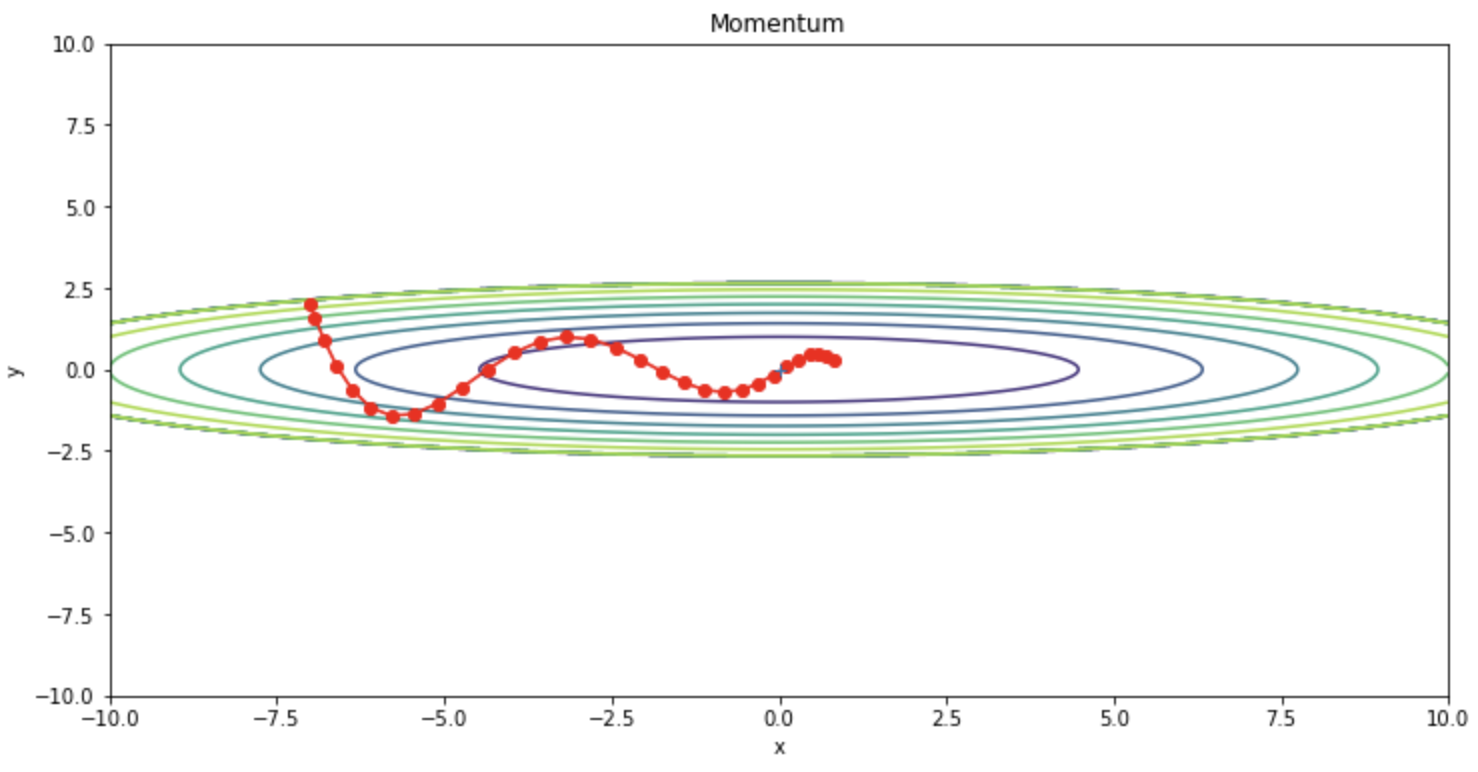
SMomentum

SGDと比較して振動を抑えられていることが確認できます。

AdaGrad

AdaGradは学習率を調整することによりSGDの振動を抑えます。以下はAdaGradの更新式になります。

v_{t+1} = v_t + (\frac{\partial L}{\partial w_t})^2

w_{t+1} = w_t - \frac{\eta}{\sqrt{v_{t+1}}}\frac{\partial L}{\partial w_t}

$v_{t+1}$ は勾配 $\frac{\partial L}{\partial w_t}$ が二乗になっており、勾配の変化が大きいときに大きくなります。また、 $(\frac{\partial L}{\partial w_t})^2$ は必ずプラスになるため、 $v_{t+1}$ は更新ごとに大きくなります。そのため、更新量 $w_{t+1}$ の学習率 $\frac{\eta}{\sqrt{v_{t+1}}}$ は振動しているときに小さくなり、また、更新ごとに小さくなっていきます。これにより、最初は広い領域で探索し、次第に探索範囲を絞るという効率の良い探索が可能になります。

AdaGradの実装コードは以下になります。

class AdaGrad:
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

optimizer = AdaGrad(lr=1.5)

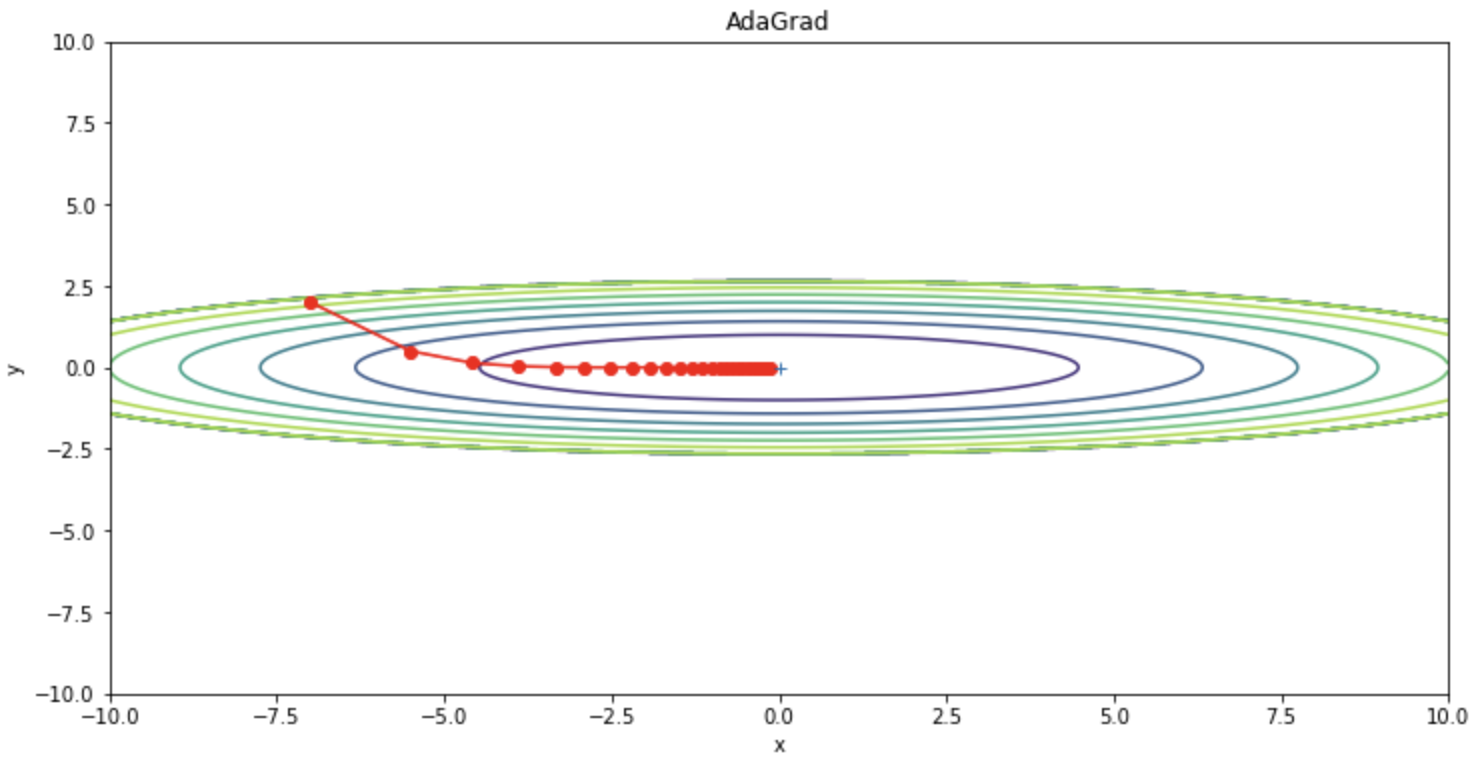
AdaGrad

SGDと比較して振動を抑えられていることが確認できます。

一方、AdaGradは、更新量が常に減少するため途中で更新量がほぼ0になってしまい、最適化がストップしてしまうことがあるというデメリットがあります。つまり、無限に学習を行うと更新量が0になり全く更新されなくなってしまいます。この問題を改善するためにRMSPropという手法が生まれました。

RMSProp

RMSPropは、AdaGradの更新量の低下により学習が停滞する問題を改善した手法になります。RMSPropの更新式は以下になります。

v_{t+1} = \rho v_t + (1- \rho) (\frac{\partial L}{\partial w_t})^2

w_{t+1} = w_t - \frac{\eta}{\sqrt{v_{t+1}}}\frac{\partial L}{\partial w_t}

$\rho$ により、過去の全ての勾配を均一に反映されるのではなく、より直近の勾配情報が反映されるように学習率を減少させます。

Adam

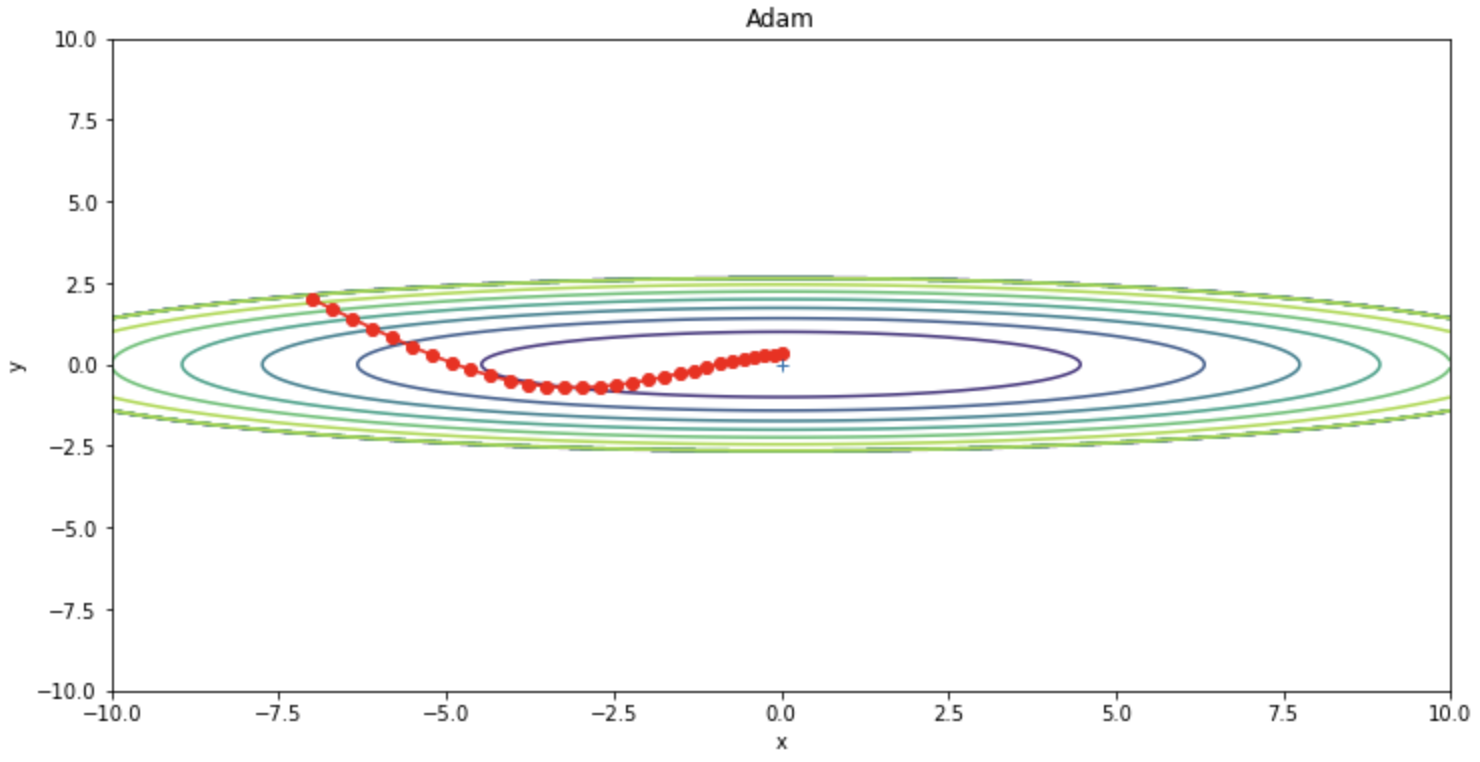
Adam（ADaptive Moment Estimation）はMomentumとRMSPropsを融合したような手法であり、よく他の最適化アルゴリズムよりも高い性能を発揮することからどにモデルにも広く使われている最適化アルゴリズムになります。次の更新式のように重みを更新します。

v_{t+1} = \beta v_t + (1- \beta)\frac{\partial L}{\partial w_t}

s_{t+1} = \rho v_t + (1- \rho) (\frac{\partial L}{\partial w_t})^2

w_{t+1} = w_t - \eta \frac{v_{t+1}}{\sqrt{s_{t+1}}}

Adamの実装コードは以下になります。

class Adam:
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

optimizer = Adam(lr=0.3)

Adam

コードまとめ

以下が今回使用したコードのまとめになります。

import numpy as np
import matplotlib.pyplot as plt
from collections import OrderedDict

class SGD:
    """SGD"""
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]

class Momentum:
    """Momentum SGD"""
    def __init__(self, lr=0.01, momentum=0.9):
        self.lr = lr
        self.momentum = momentum
        self.v = None

    def update(self, params, grads):
        if self.v is None:
            self.v = {}
            for key, val in params.items():
                self.v[key] = np.zeros_like(val)

        for key in params.keys():
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]
            params[key] += self.v[key]

class AdaGrad:
    """AdaGrad"""
    def __init__(self, lr=0.01):
        self.lr = lr
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] += grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

class RMSprop:
    """RMSprop"""
    def __init__(self, lr=0.01, decay_rate = 0.99):
        self.lr = lr
        self.decay_rate = decay_rate
        self.h = None

    def update(self, params, grads):
        if self.h is None:
            self.h = {}
            for key, val in params.items():
                self.h[key] = np.zeros_like(val)

        for key in params.keys():
            self.h[key] *= self.decay_rate
            self.h[key] += (1 - self.decay_rate) * grads[key] * grads[key]
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

class Adam:
    """Adam (http://arxiv.org/abs/1412.6980v8)"""
    def __init__(self, lr=0.001, beta1=0.9, beta2=0.999):
        self.lr = lr
        self.beta1 = beta1
        self.beta2 = beta2
        self.iter = 0
        self.m = None
        self.v = None

    def update(self, params, grads):
        if self.m is None:
            self.m, self.v = {}, {}
            for key, val in params.items():
                self.m[key] = np.zeros_like(val)
                self.v[key] = np.zeros_like(val)

        self.iter += 1
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)

        for key in params.keys():
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key])
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key])
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7)

def f(x, y):
    return x**2 / 20.0 + y**2

def df(x, y):
    return x / 10.0, 2.0*y

init_pos = (-7.0, 2.0)
params = {}
params['x'], params['y'] = init_pos[0], init_pos[1]
grads = {}
grads['x'], grads['y'] = 0, 0


optimizers = OrderedDict()
optimizers["SGD"] = SGD(lr=0.95)
optimizers["Momentum"] = Momentum(lr=0.1)
optimizers["AdaGrad"] = AdaGrad(lr=1.5)
# optimizers["RMSprop"] = RMSprop(lr=1.5)
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

for key in optimizers:
    optimizer = optimizers[key]
    x_history = []
    y_history = []
    params['x'], params['y'] = init_pos[0], init_pos[1]

    for i in range(30):
        x_history.append(params['x'])
        y_history.append(params['y'])

        grads['x'], grads['y'] = df(params['x'], params['y'])
        optimizer.update(params, grads)


    x = np.arange(-10, 10, 0.01)
    y = np.arange(-5, 5, 0.01)

    X, Y = np.meshgrid(x, y)
    Z = f(X, Y)

    # for simple contour line
    mask = Z > 7
    Z[mask] = 0

    # plot
    plt.figure(figsize=(12,6))
    # plt.subplot(2, 2, idx)
    idx += 1
    plt.plot(x_history, y_history, 'o-', color="red")
    plt.contour(X, Y, Z)
    plt.ylim(-10, 10)
    plt.xlim(-10, 10)
    plt.plot(0, 0, '+')
    plt.title(key)
    plt.xlabel("x")
    plt.ylabel("y")

plt.show()