2022-12-23

一般化線形混合モデル

Statistics

Statistical Model

一般化線形混合モデル（GLMM）とは

一般化線形混合モデル (Generalized Linear Mixed Model; GLMM）とは、GLM をさらに発展させた統計モデルであり、観測できない個体差や場所差によるばらつきを表現することができます。

観測できない個体差や場所差というのは、例えば次のようなものが挙げられます。

痛覚の個人差
同じ痛みであっても人により反応は異なります。
採点の個人差
甘い採点者もいれば辛い採点者もいます。
地域差
地域によって性質のばらつきがあります。

これらの個体差や場所差を考慮していないモデルでは、過分散を引き起こしてしまいます。過分散とは、仮定した確率分布が想定している分散よりも大きな分散となっていることを意味します。ポアソン分布を例に過分散を表すと次の図のようになります。

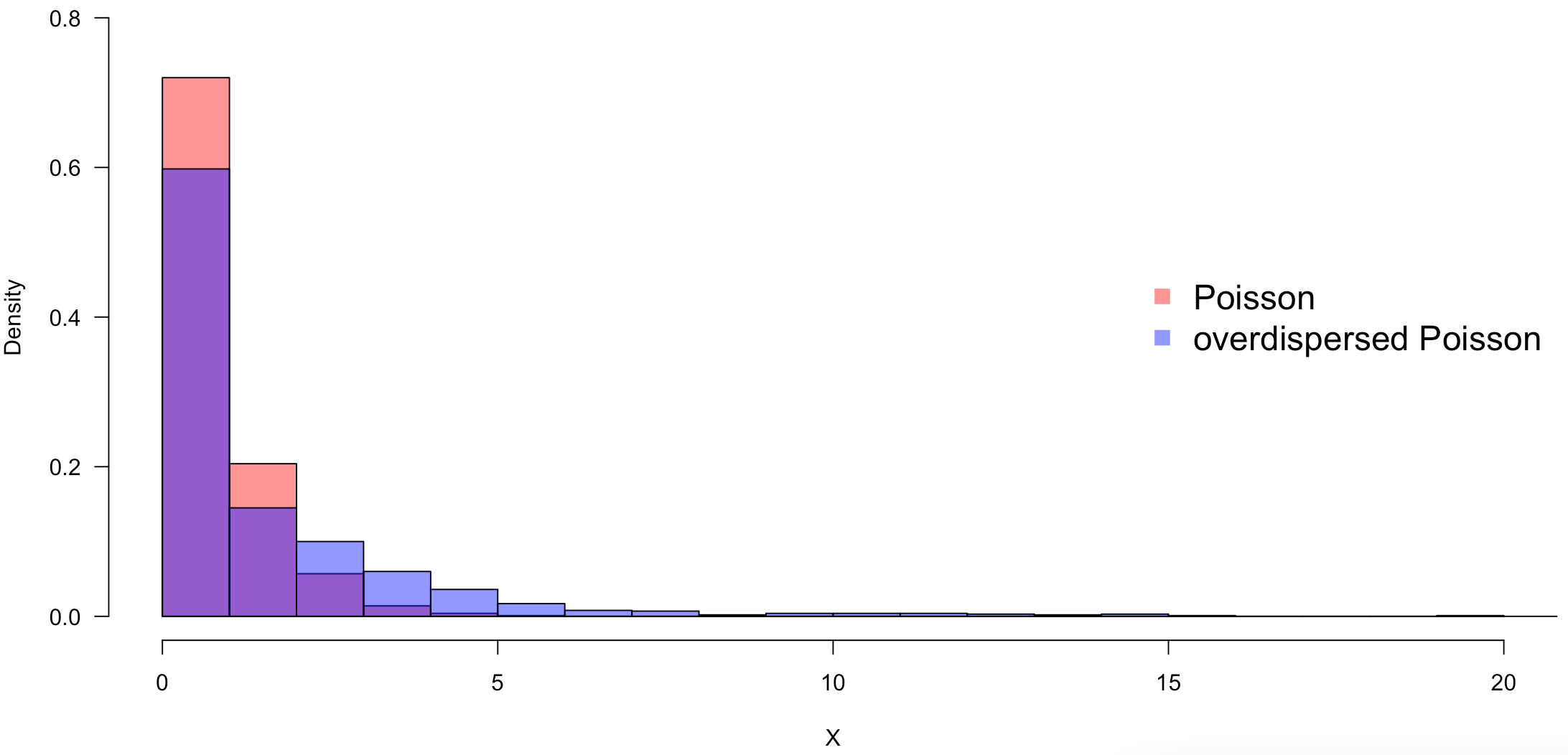
Overdispersion

個体差や場所差が発生しているとoverdispersed Poissonのように本来のポアソン分布よりも大きなばらつきとなり、個体差や場所差を考慮しないままでは観測データを上手くモデリングすることができません。

GLMMでは、説明変数の全てを観測することは不可能と判断したうえで、個体差や場所差といった原因不明のばらつきをランダム効果として扱いモデリングします。

ランダム効果

GLMMでは線形予測子にランダム効果が追加されます。例えば、個体 $i$ について個体差をランダム効果 $\eta_i$ として次のように追加します。

g(y_i) = \beta_1 + \beta_2 x_i + \cdots + \eta_i

ここで、ランダム効果 $\eta_i$ は平均0、分散 $s$ の正規分布に従うと仮定します。 $\eta_i$ の分布が正規分布に従う根拠はなく、統計モデリングに便利だという理由で正規分布としています。

パラメータの最尤推定は $\beta$ と $s$ について行われることになります。

GLMM が必要なケース

GLMMが必要かどうかの判断基準は、同じ個体や場所から何度もサンプリングしているかどうかになります。例えば、個人に対して時間経過とともに繰り返し観測したデータであるパネルデータではGLMMがよく適用されます。

GLMM の構築

grouseticks というデータセットを使ってGLMMを構築します。grouseticksはアカライチョウのヒナの頭部に付着しているダニ数の観測データであり、次のカラムで構成されています。

INDEX: (factor) chick number (observation level)
TICKS: number of ticks sampled
BROOD: (factor) brood number
HEIGHT: height above sea level (meters)
YEAR: year (-1900)
LOCATION: (factor) geographic location code
cHEIGHT: centered height, derived from HEIGHT

データの確認を行います。

> require(lme4)
> library(lme4)
> data(grouseticks)
> summary(grouseticks)

    INDEX         TICKS           BROOD         HEIGHT      YEAR        LOCATION      cHEIGHT
1      :  1   Min.   : 0.00   606    : 10   Min.   :403.0   95:117   14     : 24   Min.   :-59.241
2      :  1   1st Qu.: 0.00   602    :  9   1st Qu.:430.0   96:155   4      : 20   1st Qu.:-32.241
3      :  1   Median : 2.00   537    :  7   Median :457.0   97:131   19     : 20   Median : -5.241
4      :  1   Mean   : 6.37   601    :  7   Mean   :462.2            28     : 19   Mean   :  0.000
5      :  1   3rd Qu.: 6.00   643    :  7   3rd Qu.:494.0            50     : 17   3rd Qu.: 31.759
6      :  1   Max.   :85.00   711    :  7   Max.   :533.0            36     : 16   Max.   : 70.759
(Other):397                   (Other):356                            (Other):287

> head(grouseticks)

  INDEX TICKS BROOD HEIGHT YEAR LOCATION   cHEIGHT
1     1     0   501    465   95       32  2.759305
2     2     0   501    465   95       32  2.759305
3     3     0   502    472   95       36  9.759305
4     4     0   503    475   95       37 12.759305
5     5     0   503    475   95       37 12.759305
6     6     3   503    475   95       37 12.759305

> plot(TICKS ~ HEIGHT, las=1)

TICKS and HEIGHT

ポアソン回帰（ランダム効果なし）

今回はポアソン回帰モデルを構築します。平均のダニ数 $\lambda_i$ を使って対数リンク関数を次のように表します。

\log \lambda_i = \beta_1 + \beta_2 d_i

ここで、 $d_i$ はYearのダミー変数です。

次のコードでパラメータを推定することができます。

> fit_glm <- glm(TICKS ~ YEAR, family=poisson(), data=grouseticks)
> summary)(fit_glm)

Call:
glm(formula = TICKS ~ YEAR, family = poisson(), data = grouseticks)

Deviance Residuals:
    Min       1Q   Median       3Q      Max
-4.7110  -2.8888  -1.5183   0.7139  17.1467

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  1.78318    0.03790   47.05   <2e-16 ***
YEAR96       0.62348    0.04492   13.88   <2e-16 ***
YEAR97      -1.64109    0.08977  -18.28   <2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 5847.5  on 402  degrees of freedom
Residual deviance: 4549.4  on 400  degrees of freedom
AIC: 5486.4

Number of Fisher Scoring iterations: 6

AICは5486.4となっています。

ポアソン回帰（ランダム効果あり）

ランダム効果を考慮したポアソン回帰モデルを構築します。

Random intercept model

LOCATIONによる場所 $j$ のランダム効果 $\eta_j$ を加えて平均のダニ数 $\lambda_i$ を次のように表します。

\log \lambda_i = \beta_1 + \beta_2 d_i + \eta_j, \quad \eta_j \sim N(0, s^2)

このモデルは、ランダム効果が切片に入っていることからrandom intercept modelとも呼ばれます。

次のコードで $\beta$ と $s$ を推定することができます。ランダム効果を切片に与えたい場合はTICKS ~ YEAR + (1 | LOCATION)のように記述します。

> fit_glmm <- glmer(TICKS ~ YEAR + (1 | LOCATION), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (1 | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2306.3   2322.3  -1149.1   2298.3      399

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6399 -0.8844 -0.4708  0.8543  5.5757

Random effects:
 Groups   Name        Variance Std.Dev.
 LOCATION (Intercept) 1.644    1.282
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  0.64992    0.18319   3.548 0.000388 ***
YEAR96       0.94371    0.08492  11.113  < 2e-16 ***
YEAR97      -1.43642    0.12298 -11.681  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.295
YEAR97 -0.241  0.520

AICが2306.3となり、ランダム効果がないモデルよりも大きく改善されました。

LOCATIONのランダム効果の分散は1.644となっています。randf()関数で全てのLOCATIONのランダム効果を確認することができます。

> ranef(fit_glmm)

$LOCATION
   (Intercept)
1   1.24539318
2   0.92293852
3  -0.93190888
.
.
.
61 -1.35144088
62 -0.95446024
63 -1.15277383

with conditional variances for “LOCATION”

1から63はLOCATIONの値です。1のinterceptは1.24539318、3のinterceptは-0.93190888となっています。解釈としては、LOCATION 1はLOCATION 3よりも相対的にダニの数が多いということになります。

さらにINDEXによるランダム効果 $\tau_i$ を加えることも可能です。

\log \lambda_i = \beta_1 + \beta_2 d_i + \eta_j + \tau_i, \quad \eta_j \sim N(0, s^2), \tau_i \sim N(0, \sigma^2)

> fit_glmm <- glmer(TICKS ~ YEAR + (1 | LOCATION) + (1 | INDEX), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (1 | LOCATION) + (1 | INDEX)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  1863.9   1883.9   -927.0   1853.9      398

Scaled residuals:
    Min      1Q  Median      3Q     Max
-1.5003 -0.5933 -0.1154  0.2723  2.3743

Random effects:
 Groups   Name        Variance Std.Dev.
 INDEX    (Intercept) 0.5081   0.7128
 LOCATION (Intercept) 1.4679   1.2116
Number of obs: 403, groups:  INDEX, 403; LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.2774     0.2107   1.316    0.188
YEAR96        1.2578     0.1821   6.906 4.97e-12 ***
YEAR97       -1.0856     0.2010  -5.400 6.67e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.536
YEAR97 -0.439  0.552

AICが1863.9となり、さらに改善されました。

LOCATIONのランダム効果の分散は1.4679、 INDEXのランダム効果の分散は0.5081となっています。INDEXの方がLOCATIONよりもランダム効果が小さいことが分かります。

Random coefficient model

LOCATIONによるランダム効果 $\eta_j$ を切片だけでなく係数にも加えてみます。

\log \lambda_i = (\beta_1 + \eta_{1j}) + (\beta_2 + \eta_{2j}), \quad \eta_{1j} \sim N(0, s^2), \quad \eta_{2j} \sim N(0, \sigma^2)

このモデルは、ランダム効果が係数に入っていることからrandom coefficient modelとも呼ばれます。

次のコードで $\beta$ 、 $s$ 、 $\sigma$ を推定することができます。ランダム効果を切片と係数に与えたい場合はTICKS ~ YEAR + (YEAR | LOCATION)のように記述します。

> fit_glmm <- glmer(TICKS ~ YEAR + (YEAR | LOCATION), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (YEAR | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2266.7   2302.7  -1124.3   2248.7      394

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6442 -0.8112 -0.4797  0.8437  5.5779

Random effects:
 Groups   Name        Variance Std.Dev. Corr
 LOCATION (Intercept) 2.3583   1.5357
          YEAR96      0.6002   0.7747   -0.70
          YEAR97      0.6735   0.8207   -0.80  0.46
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.3273     0.2674   1.224  0.22083
YEAR96        1.3094     0.2542   5.152 2.58e-07 ***
YEAR97       -0.7578     0.2909  -2.605  0.00918 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.746
YEAR97 -0.668  0.553

ただし、この推定は $\eta_{1j}$ と $\eta_{2j}$ の相関を仮定しているモデルになります。両パラメータが互いに独立だと仮定したモデルを当てはめたい場合はTICKS ~ YEAR + (1 | LOCATION) + (0 + YEAR | LOCATION)のように記述します。

> fit_glmm <- glmer(TICKS ~ YEAR + (1 | LOCATION) + (0 + YEAR | LOCATION), family="poisson", data=grouseticks)
> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (1 | LOCATION) + (0 + YEAR | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2268.7   2308.7  -1124.3   2248.7      393

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6442 -0.8112 -0.4797  0.8437  5.5779

Random effects:
 Groups     Name        Variance Std.Dev. Corr
 LOCATION   (Intercept) 0.4151   0.6443
 LOCATION.1 YEAR95      1.9431   1.3939
            YEAR96      0.8755   0.9357   0.85
            YEAR97      0.6006   0.7750   0.87 0.54
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.3274     0.2674   1.224  0.22081
YEAR96        1.3094     0.2542   5.152 2.58e-07 ***
YEAR97       -0.7578     0.2909  -2.605  0.00918 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.746
YEAR97 -0.668  0.553

また、TICKS ~ YEAR + (0 + YEAR | LOCATION)のように記述することでランダム効果を係数にのみ追加することも可能です。

> fit_glmm <- glmer(TICKS ~ YEAR + (0 + YEAR | LOCATION), family="poisson", data=grouseticks)

Warning message:
In checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv,  :
  Model failed to converge with max|grad| = 0.0139508 (tol = 0.002, component 1)

> summary(fit_glmm)

Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
 Family: poisson  ( log )
Formula: TICKS ~ YEAR + (0 + YEAR | LOCATION)
   Data: grouseticks

     AIC      BIC   logLik deviance df.resid
  2266.7   2302.7  -1124.3   2248.7      394

Scaled residuals:
    Min      1Q  Median      3Q     Max
-6.6442 -0.8114 -0.4793  0.8432  5.5778

Random effects:
 Groups   Name   Variance Std.Dev. Corr
 LOCATION YEAR95 2.363    1.537
          YEAR96 1.291    1.136    0.87
          YEAR97 1.016    1.008    0.87 0.70
Number of obs: 403, groups:  LOCATION, 63

Fixed effects:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   0.3276     0.2676   1.224  0.22093
YEAR96        1.3099     0.2543   5.151 2.59e-07 ***
YEAR97       -0.7566     0.2908  -2.601  0.00929 **
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Correlation of Fixed Effects:
       (Intr) YEAR96
YEAR96 -0.746
YEAR97 -0.669  0.554
optimizer (Nelder_Mead) convergence code: 0 (OK)
Model failed to converge with max|grad| = 0.0139508 (tol = 0.002, component 1)

R コード

ポアソン分布ん過分散を図示するRコードは以下になります。

> set.seed(1)
> hist(Y1 <- rpois(1000, 1), breaks=seq(0, 20), col="#FF00007F", freq=F, ylim=c(0, 0.8), las=1,
     main="", xlab="X")
> hist(Y2 <- rpois(1000, 1 * exp(rnorm(1000, mean=0, sd=1))), col="#0000FF7F", add=T, freq=F, breaks=seq(0, 100))
> legend("right", legend=c("Poisson", "overdispersed Poisson"), pch=15, col=c("#FF00007F", "#0000FF7F"),
       bty="n", cex=1.5)