指数分布とは

指数分布とは単位時間当たりに平均 \lambda 回起こる事象が次に発生する時間 x が従う確率分布です。指数分布は次のような例に用いられます。

• 1時間に平均20回電話が鳴るコールセンターで、次に電話が鳴るまでの時間
• 2年間に1回発生する災害が次に発生するまでの時間

指数分布の確率密度関数は次のように表すことができます。

\lambda は単位時間においてその事象が起こる平均の回数であり、x がその事象が起こるまでの期間になります。

\lambda が \frac{1}{6}、\frac{1}{2}、1、2の場合の指数分布は次のようになります。

\lambda の値が小さいほど減少は緩やかになり、また、\lambda の値に依存せずに必ず単調減少していることが分かります。

指数分布の期待値と分散

指数分布の期待値、分散はそれぞれ以下になります。

指数分布の無記憶性

確率変数 X が指数分布に従い、m, n > 0 とすると、次の式が成り立ちます。

上式は将来の事象発生までの時間がその過去の事象の有無に依存しないということを意味しています。この性質を無記憶性（Memoryless）といいます。指数分布は無記憶性を持つ唯一の連続分布になります。

ポアソン分布との関係

指数分布はある事象が起こるまでの時間が従う確率分布であり、ポアソン分布は単位時間内に事象が起こる回数が従う確率分布です。つまり、同じ事象を指数分布は「時間」で捉え、ポアソン分布は「回数」で捉えます。

Python コード

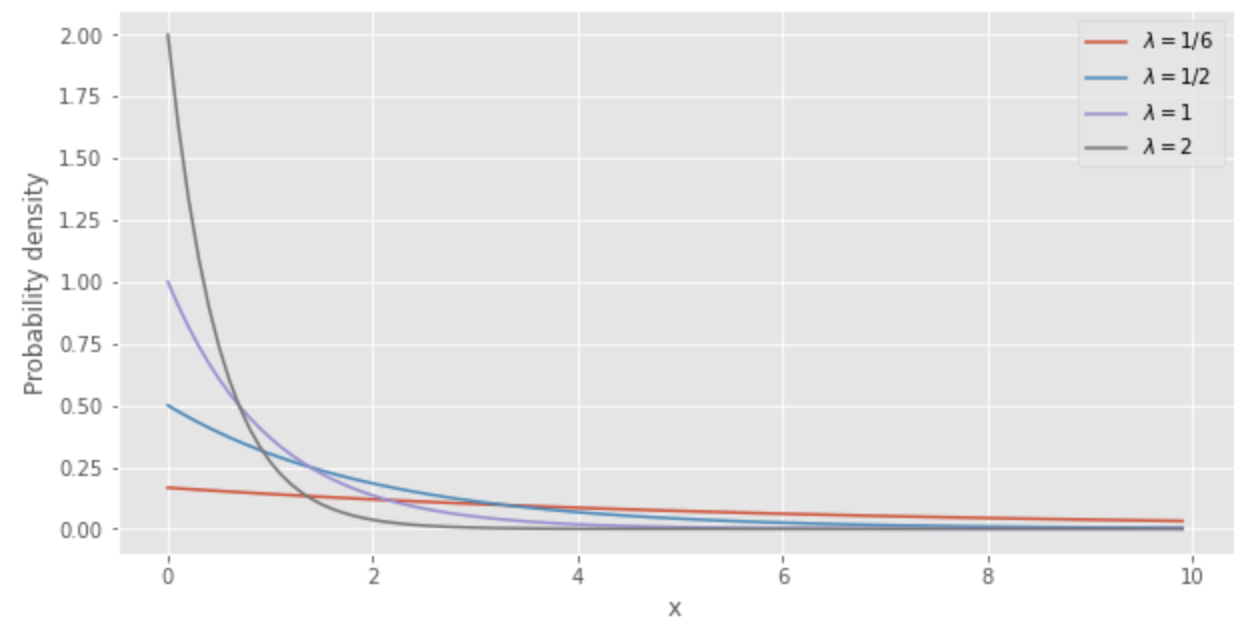
次のPythonコードで指数分布を描画することができます。

from scipy.stats import expon
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

plt.style.use('ggplot')
plt.figure(figsize=(10,5))

x = np.arange(0, 10, 0.1)
y_1_6 = expon.pdf(x=x, scale=6)
y_1_2 = expon.pdf(x=x, scale=2)
y_1 = expon.pdf(x=x, scale=1)
y_2 = expon.pdf(x=x, scale=1/2)
plt.plot(x, y_1_6, label='$\lambda=1/6$')
plt.plot(x, y_1_2, label='$\lambda=1/2$')
plt.plot(x, y_1, label='$\lambda=1$')
plt.plot(x, y_2, label='$\lambda=2$')
plt.legend()
plt.xlabel("x")
plt.ylabel("Probability density")