2022-04-12

Causal Inference

What is Causal Inference

Causal inference is a methodological approach to understand and analyze cause-and-effect relationships. It seeks to uncover the causal relationships between variables, events, or interventions in order to determine the impact of one factor on another. By exploring these relationships, causal inference enables researchers to go beyond mere correlation and uncover the underlying mechanisms that drive observable phenomena.

At its core, causal inference aims to answer questions such as "What would happen if?" or "What is the effect of?" These questions delve into the realm of causality, seeking to understand the potential outcomes under different scenarios. While correlation can provide valuable insights into the association between variables, causal inference goes a step further by identifying and quantifying the direct influence of one variable on another.

Causal inference acknowledges that simple correlation does not imply causation. Just because two variables are observed to be related does not necessarily mean that one is causing the other. There may be confounding factors, hidden variables, or complex dynamics at play. To address these challenges, causal inference employs rigorous methodologies, statistical models, and experimental designs to establish causality.

Basic Concepts of Causal Inference

I will introduce the foundational concepts underpinning causal inference. The two key concepts to be addressed are confounding variables and the counterfactuals.

Confounding Variables

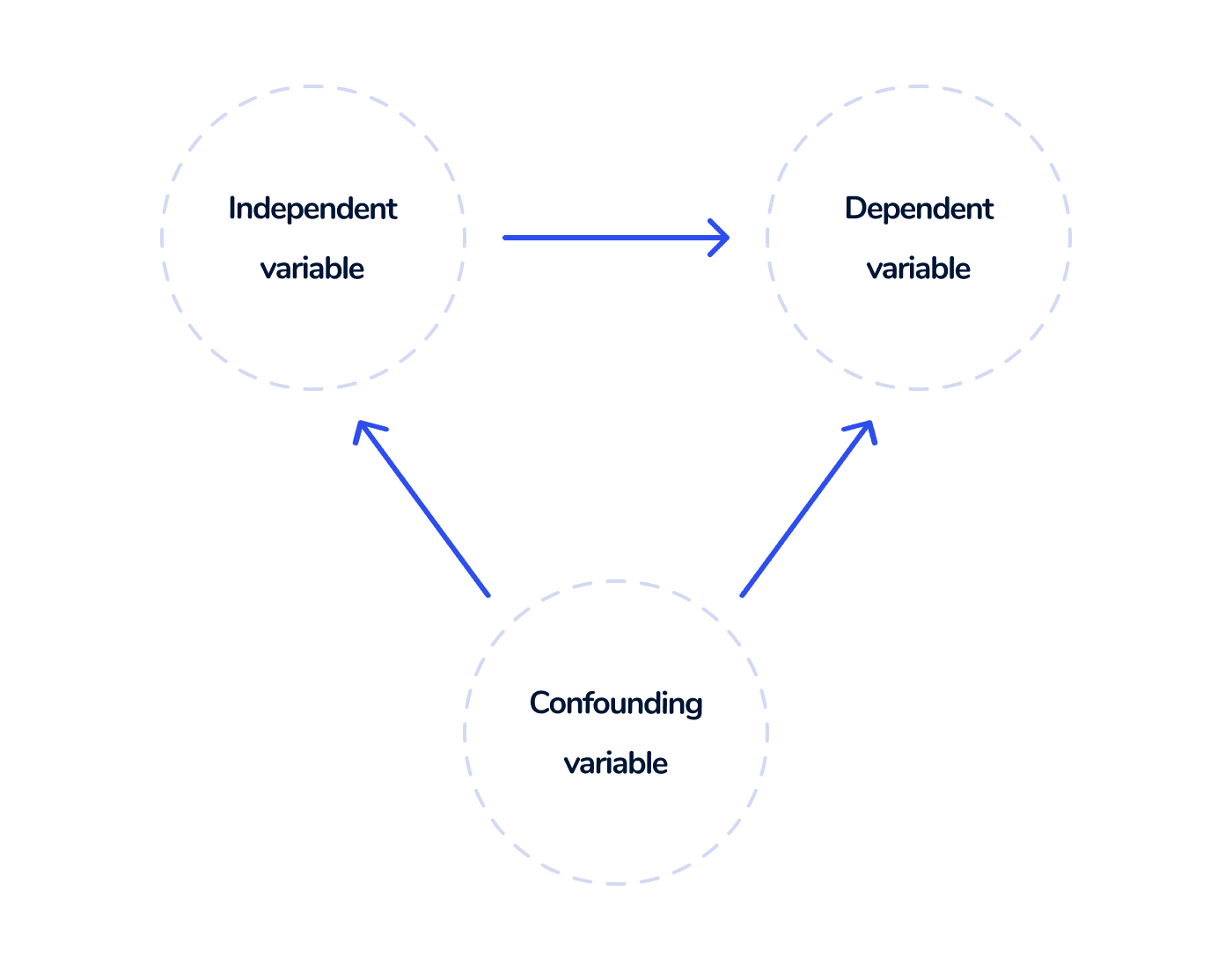
In the realm of causal inference, confounding variables play a significant role. Confounders are variables that are associated with both the independent variable (treatment) and the dependent variable (outcome) in a study. These confounders can introduce biases and obscure the true relationship between the treatment and outcome.

Confounding Variable: Easy Guide + Examples

For instance, let's consider a study investigating the impact of a new drug on patient outcomes. Age could act as a confounding variable because it is related to both the administration of the drug and the health condition of the patients. If age is not properly controlled for, it can create a false impression that the drug has a strong relationship with the outcomes, when in reality, age might be the driving factor behind the observed effects.

Controlling for confounding variables is crucial in causal inference to ensure that the observed relationship between the treatment and outcome accurately reflects the causal effect of interest. Various statistical techniques and study designs, such as randomization and regression analysis, are employed to address the issue of confounding variables and minimize their impact on causal inference.

Counterfactuals

Counterfactuals are a fundamental concept in causal inference. They involve imagining alternative scenarios or conditions that did not occur in reality. Counterfactuals help us answer questions about what would have happened if the treatment or intervention had been different or had not taken place at all.

In a counterfactual framework, we compare the actual observed outcome (factual) with the outcome that would have occurred under a different scenario (counterfactual). By examining the difference between these two outcomes, we can estimate the causal effect of the treatment or intervention.

However, a significant challenge in causal inference is that we can never observe both the factual and counterfactual outcomes for the same unit simultaneously. This is known as the "fundamental problem of causal inference." To overcome this challenge, various techniques and statistical methods, such as propensity score matching or instrumental variables, are employed to estimate the unobserved counterfactual outcomes.

Counterfactuals allow us to disentangle the effects of different treatments, policies, or interventions and understand their causal impact on the outcomes of interest. They help us move beyond mere association and provide a framework for making causal claims based on evidence and careful reasoning.

Techniques for Causal Inference

We discuss the methods for causal inference that have been rigorously tested and applied in numerous fields to uncover causal relationships.

Randomized Controlled Trials (RCTs)

Randomized Controlled Trials are the gold standard for determining causal relationships. In an RCT, subjects are randomly assigned to either the treatment group or the control group, which helps mitigate the issue of confounding variables. The random assignment ensures that, on average, the treatment and control groups are comparable, thus isolating the effect of the treatment.

Instrumental Variables (IV)

The instrumental variables approach is a method used when randomization is not feasible. An instrumental variable is a variable that affects the treatment but has no direct effect on the outcome, except through the treatment. This technique allows us to isolate the causal effect of the treatment on the outcome.

Regression Discontinuity Design (RDD)

RDD is used when treatment assignment is determined by whether an observed variable exceeds a certain threshold. Close to the threshold, individuals just below and just above are likely to be similar, which creates a kind of natural experiment where we can compare outcomes across the threshold to estimate the treatment effect.

Difference in Differences (DID)

DiD is a statistical technique that calculates the effect of a treatment (such as a policy change or a new program) over time. It compares the change in outcomes before and after the treatment in a group that received the treatment to a group that didn’t. This technique assumes that, without the treatment, the trends over time would have been the same in the two groups.

Propensity Score Matching

Propensity Score Matching is a technique that tries to estimate the effect of a treatment by matching treated units with similar untreated units based on their propensity to be treated. The propensity score is typically estimated using logistic regression.

Causal Graphs and Directed Acyclic Graphs (DAGs)

Causal graphs, including Directed Acyclic Graphs (DAGs), provide a visual representation of causal relationships among variables. In a DAG, nodes represent variables, and directed edges between nodes represent causal relationships. DAGs provide a way to reason about confounding, selection bias, and other complexities in causal analysis.

Causal Trees and Forests

These are modern machine learning methods designed for causal inference. Causal trees split on features not to predict an outcome directly (as in a standard decision tree) but to identify differences in treatment effects. Causal forests are an extension of this idea, where predictions are made based on an ensemble of causal trees, improving the robustness and accuracy of the causal effect estimation.

Applications of Causal Inference in Various Fields

The causal inference has profound, tangible impacts across a spectrum of fields, serving as a linchpin for informed decision-making and the generation of insights. Let's explore some of these applications.