What is Instrumental Variables

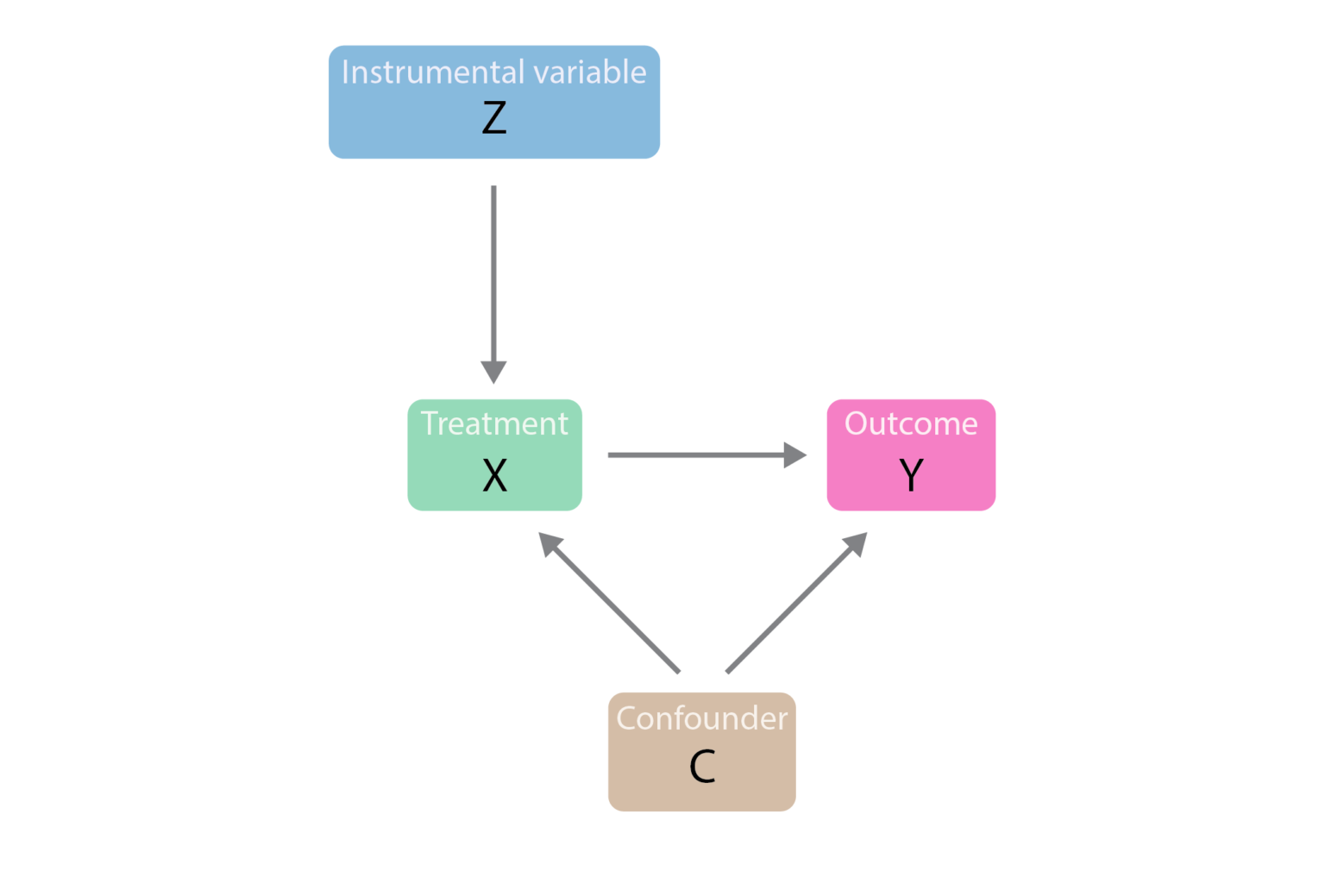
An instrumental variable is a tool used in statistical analysis to isolate the causal effect of one variable on another. It is a third variable that is used to control the endogeneity problem in regression analysis, where an independent variable is correlated with the error term. This correlation typically arises due to omitted variables, simultaneity, or measurement errors.

Let's consider an example to illustrate the concept. Imagine you are studying the effect of studying hours on students' grades. There may be an unobserved variable, such as inherent ability, that affects both studying hours and grades, causing a correlation between your independent variable (studying hours) and the error term. A possible instrumental variable could be the distance from the student's home to the library. This variable likely influences the number of hours a student studies but is not directly related to a student's grade (except through its impact on studying hours).

How Instrumental Variables Are Identified

Identifying suitable instrumental variables is a crucial step and perhaps one of the most challenging in any causal analysis. The choice of an instrumental variable is generally based on theoretical reasoning and practical considerations. Here are the two fundamental criteria an instrumental variable must satisfy:

• The instrument must be correlated with the endogenous explanatory variable, also known as the relevance condition. This correlation is crucial because the strength of the instrument directly impacts the precision of the estimates. If the correlation is weak, the so-called 'weak instruments problem' may arise, leading to biased and inconsistent estimates.

• The instrument must not be correlated with the error term in the regression model, also known as the exogeneity condition. In other words, it should not have any direct effect on the dependent variable apart from through the endogenous explanatory variable.

While these conditions may seem straightforward, they can be quite challenging to verify in practice. The first condition can be tested empirically by checking the correlation between the proposed instrument and the endogenous variable. However, the second condition is generally untestable as it involves unobservable variables, hence it often relies on a convincing argument or an understanding of the underlying processes of the system being studied.

Instrumental Variables for Causal Inference

The instrumental variable approach is a tool for causal inference, primarily because it enables researchers to account for confounding variables that are unobserved and hence not directly controllable. By using an instrumental variable that is correlated with the explanatory variable but not correlated with the unobserved confounders or the error term, researchers can isolate the causal effect of the explanatory variable on the outcome variable.

3 Real-World Examples of Using Instrumental Variables

Derivation of Instrumental Variables

The derivation of instrumental variables hinges upon the two-stage least squares (2SLS) regression, a common statistical method for estimating causal effects in the presence of endogeneity. The idea is to first predict the endogenous explanatory variable using the instrumental variable, and then use these predicted values to estimate the causal effect.

Let's begin by considering a simple linear regression model:

y = \beta_0 + \beta_1 x + u

In this model, y is the outcome variable, x is the explanatory variable, \beta_0 and \beta_1 are the parameters of interest, and u is the error term. We want to estimate \beta_1, which is the causal effect of x on y. However, suppose x is correlated with u due to omitted variables, simultaneity, or measurement errors, which creates an endogeneity problem and biases our estimate of \beta_1.

Suppose z is an instrumental variable for x that satisfies the relevance condition (z is correlated with x) and the exogeneity condition (z is uncorrelated with u). The instrumental variable approach involves the following two steps:

1. Regress x on z (and possibly other exogenous variables), which yields the predicted values of x, denoted by \hat{x}:

\hat{x} = \pi_0 + \pi_1 z + v

where \pi_0 and \pi_1 are the parameters to be estimated and v is the error term.

2. Regress y on \hat{x} (and possibly other exogenous variables), which yields the instrumental variable estimates of \beta_0 and \beta_1:

y = \beta_0 + \beta_1 \hat{x} + \hat{u}

where \hat{\beta_0} and \hat{\beta_1} are the parameters of interest and \hat{u} is the error term.

Through these steps, we are effectively 'cleansing' x of its correlation with the error term u by replacing it with \hat{x}, which is constructed using only z and is therefore uncorrelated with u. The resulting estimate of \beta_1, denoted by \hat{\beta_1}, is then an unbiased and consistent estimate of the causal effect of x on y, given that z is a valid instrument.

It is important to note that the instrumental variable estimates only identify the local average treatment effect (LATE), which is the effect of the explanatory variable on the subpopulation of "compliers" who change their behavior in response to changes in the instrumental variable. This effect may differ from the average treatment effect (ATE), which is the average effect of the explanatory variable on the entire population.

References

https://quantifyinghealth.com/examples-of-instrumental-variables/
https://www.statology.org/instrumental-variables/