勾配消失問題とは

勾配消失問題とは、深層ニューラルネットワークのトレーニング中に発生するよく知られた問題です。この問題は、ネットワークの層を逆方向に伝播する際に使用される勾配が非常に小さくなる場合に発生します。これにより、ネットワークの初期層がトレーニング中にほとんど更新を受けず、収束が遅く、パフォーマンスが低下することがあります。

勾配消失問題を理解するためには、深層ニューラルネットワークをトレーニングするために使用されるバックプロパゲーションアルゴリズムを考慮すると役立ちます。トレーニング中、バックプロパゲーションアルゴリズムは、ネットワークのパラメータに関する損失関数の勾配を計算します。この勾配は、パラメータを更新するために使用され、ネットワークがトレーニングデータから学習することができます。

しかし、深層ニューラルネットワークでは、勾配がネットワークの層を逆方向に伝播する際に非常に小さくなる場合があります。これは、勾配が各層で重み行列によって乗算され、多くの小さな数値の積が非常に小さくなることがあるためです。その結果、ネットワークの初期層はトレーニング中にほとんど更新を受けず、収束が遅く、パフォーマンスが低下することがあります。

勾配消失問題の原因

活性化関数の選択

勾配消失問題に寄与する重要な要因の1つは、活性化関数の選択です。シグモイド関数や双曲線正接 (tanh) 関数などの活性化関数は、出力が入力のわずかな変化に対して鈍感になる飽和現象に陥りやすい傾向があります。この飽和現象により、勾配が非常に小さくなる場合があり、特に多層の深いネットワークでは深刻な問題となります。その結果、ネットワークの初期層はトレーニング中にほとんど更新を受けず、収束が遅く、パフォーマンスが低下することがあります。

この問題に対処するために、シグモイド関数や双曲線正接関数よりも飽和現象に陥りにくい代替の活性化関数が提案されています。例えば、ReLU関数が挙げられます。ReLU関数は単純な形式で計算が容易であり、多くの深層学習アプリケーションで人気があります。また、最近の研究では、Swish関数などのより複雑な活性化関数が探究され、深層ニューラルネットワークのパフォーマンスが改善されたことが報告されています。

ネットワークの深さ

勾配消失問題に寄与する別の要因は、ネットワークの深さです。ネットワークの層数が増えると、勾配はより多くの層を逆方向に伝播する必要があり、勾配が非常に小さくなる可能性が高くなります。そのため、勾配が役に立たなくなるほど小さくなり、深層ニューラルネットワークのトレーニングが困難になる場合があります。

この問題に対処するために、スキップ接続などのテクニックが提案されています。スキップ接続は、1つの層の出力を後の層の入力に加えることで、勾配がより容易にネットワークを伝播することを可能にします。また、バッチ正規化などの正規化技術は、勾配を安定させ、より容易にネットワークを伝播することができます。

重みの初期化

最後に、ネットワークの重みの初期化も勾配消失問題に寄与することがあります。重みが大きな値で初期化されると、勾配が層を逆方向に伝播する際に非常に小さくなることがあります。これは、大きな数値の積が重みの符号に応じて非常に大きくまたは非常に小さくなる可能性があるためです。

この問題に対処するために、Xavier初期化などの重みの初期化戦略が提案されています。Xavier初期化は、各層の初期重みをレイヤーの入力数の平方根に比例するように設定します。これにより、初期勾配が適切な大きさになり、ネットワークをより容易に伝播できるようになります。

勾配消失問題の影響

トレーニング中の収束の遅さ

勾配消失問題のもっとも大きな影響の1つは、トレーニング中の収束の遅さです。勾配がネットワークを逆方向に伝播する際に非常に小さくなる場合、ネットワークの初期層はトレーニング中にほとんど更新を受けません。これにより、収束が遅くなり、ネットワークを効果的にトレーニングすることが困難になる場合があります。場合によっては、ネットワークが収束せず、トレーニングデータから学習することができなくなることもあります。

サブオプティマルな解の可能性

勾配消失問題の別の影響は、ネットワークがサブオプティマルな解に陥る可能性があることです。勾配が非常に小さくなると、ネットワークは効果的に可能な解の全てを探索することができなくなる場合があります。その結果、最適解よりも劣ったサブオプティマルな解に収束することがあります。これにより、テストデータでのパフォーマンスが悪化し、ネットワークの効果が制限される場合があります。

勾配消失による過学習

最後に、勾配消失問題は過学習に寄与することもあります。勾配が非常に小さくなると、ネットワークはトレーニングデータを過剰に学習し、新しいデータに汎化することができなくなる場合があります。その結果、テストデータでのパフォーマンスが悪化し、ネットワークの実用性が制限されることがあります。

勾配消失問題のデモンストレーション

この章では、アクティベーション分布を示すことで、勾配消失問題をデモンストレーションします。

PyTorchライブラリを使用して、MNISTデータセットを使用した深層ニューラルネットワークアーキテクチャを実装します。MNISTデータセットは、手書き数字の広く使用されている公開データセットです。目標は、数字を正しく分類するための深層ニューラルネットワークをトレーニングすることです。複数の隠れ層を持つ深層ニューラルネットワークアーキテクチャを使用し、各層でシグモイド活性化関数を使用します。

勾配消失問題に対処するテクニックなしで、標準的なアプローチを使用してネットワークをトレーニングします。次に、勾配消失問題の影響を示すために、ネットワークの各層での活性化分布を示します。

以下は、PyTorchコードで、深層ニューラルネットワークアーキテクチャを定義し、ネットワークをトレーニングするものです。

import torch
import torch.nn as nn
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms

# Load MNIST dataset
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.5,), (0.5,))])
trainset = torchvision.datasets.MNIST(root='./data', train=True, download=True, transform=transform)
trainloader = torch.utils.data.DataLoader(trainset, batch_size=100, shuffle=True, num_workers=2)

# Define deep network with sigmoid activation
class DeepSigmoidNet(nn.Module):
    def __init__(self):
        super(DeepSigmoidNet, self).__init__()
        self.fc1 = nn.Linear(28 * 28, 1000)
        self.fc2 = nn.Linear(1000, 1000)
        self.fc3 = nn.Linear(1000, 1000)
        self.fc4 = nn.Linear(1000, 1000)
        self.fc5 = nn.Linear(1000, 1000)
        self.fc6 = nn.Linear(1000, 10)

    def forward(self, x):
        x = x.view(-1, 28 * 28)
        x = torch.sigmoid(self.fc1(x))
        x = torch.sigmoid(self.fc2(x))
        x = torch.sigmoid(self.fc3(x))
        x = torch.sigmoid(self.fc4(x))
        x = torch.sigmoid(self.fc5(x))
        x = self.fc6(x)
        return x

# Instantiate the network, loss function, and optimizer
net = DeepSigmoidNet()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(net.parameters(), lr=0.01, momentum=0.9)

# Train the network
for epoch in range(10):
    running_loss = 0.0
    for i, data in enumerate(trainloader, 0):
        inputs, labels = data
        optimizer.zero_grad()
        outputs = net(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()
        running_loss += loss.item()

    # Print average loss per epoch
    print(f"Epoch {epoch + 1}, Loss: {running_loss / (i + 1)}")

# Collect gradients for histogram
gradients = []
for p in net.parameters():
    if p.grad is not None:
        gradients.append(p.grad.view(-1).cpu().numpy())

勾配値の分布を描画します。

import numpy as np
import matplotlib.pyplot as plt

plt.style.use('ggplot')

# Create a histogram of the gradients
plt.hist(gradients, bins=100, range=(-1, 1), log=True, color='blue', alpha=0.5)
plt.xlabel('Gradient Values')
plt.ylabel('Frequency')
plt.title('Histogram of Gradient Values in Deep Sigmoid Network')
plt.show()

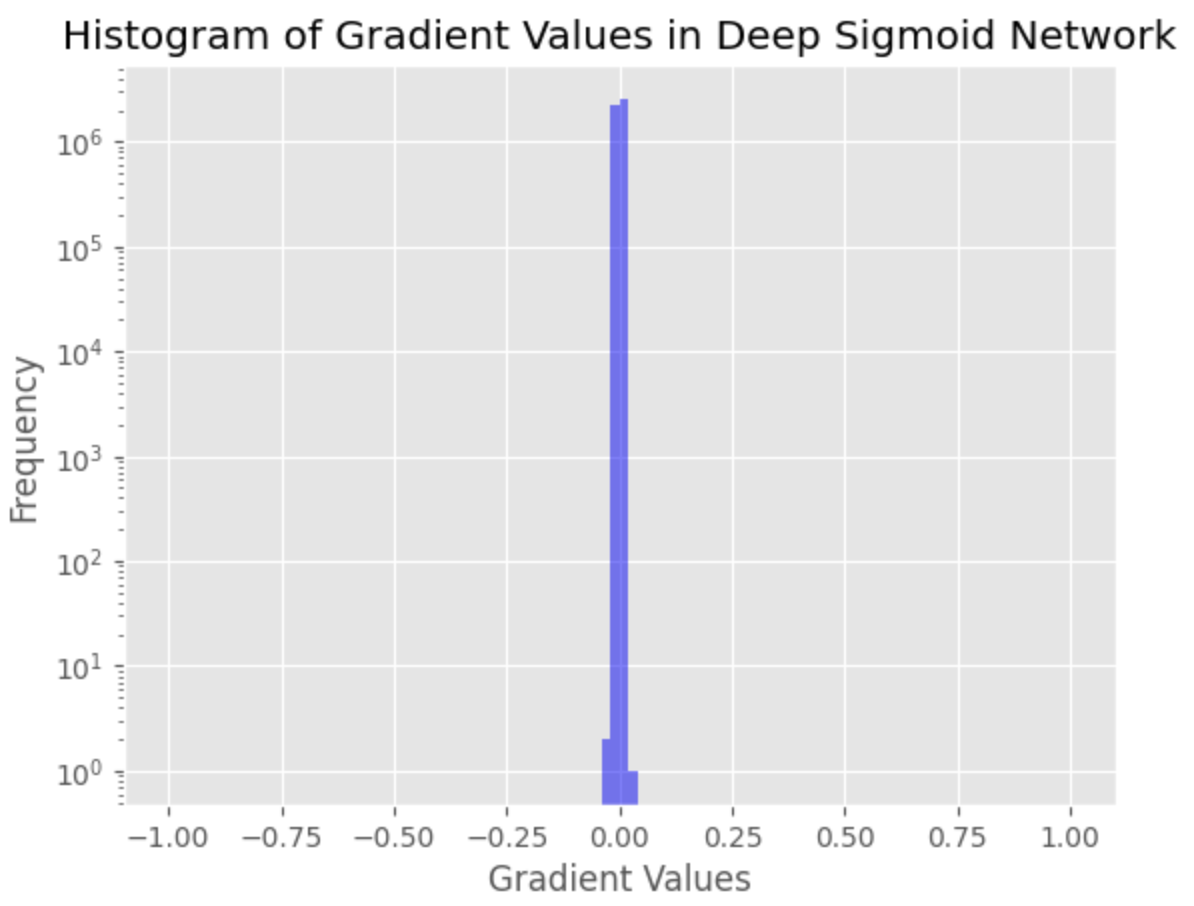
このヒストグラムは、非常に小さい勾配値が多数存在することを示しています。これは、ネットワークの初期層の勾配がほとんど消失していることを意味し、収束が悪化し、ネットワークをトレーニングするのが困難になる可能性があることを示しています。