2022-10-25

バッチ正規化

バッチ正規化とは

バッチ正規化は、深層学習における画期的な技術の一つで、トレーニングを加速し、モデルの収束を改善し、適切な学習率や重み初期化を選択するプロセスを簡素化することができます。2015年にIoffeとSzegedyによって提案されたバッチ正規化は、ニューラルネットワーク内の各層への入力分布の変化に起因する内部共変量シフトの問題に対処します。

バッチ正規化の主な目的は、ニューラルネットワーク内の各層の入力分布を安定化させることによって、より迅速かつ安定したトレーニングを可能にすることです。これは、各ミニバッチ内の各特徴量の平均値と分散を使用して各層のアクティベーションを正規化することで達成されます。正規化後、データはトレーニング中に更新される学習可能なパラメータを使用してスケーリングおよびシフトされます。これにより、モデルは広範な入力分布を表現できます。

バッチ正規化の重要性

バッチ正規化の導入により、深層学習の分野に大きな影響を与え、様々な深層学習アーキテクチャの設計において標準的なコンポーネントとなりました。この技術は、次のような多数の利点を提供するため、広く採用されています。

トレーニングの高速化
入力分布を安定化することにより、バッチ正規化はより高い学習率の使用を可能にし、トレーニングプロセスを加速します。
モデルの収束の改善
層のアクティベーションを正規化することで、勾配消失および勾配爆発の問題を防ぎ、モデルの収束を促進します。
初期化への感度低減
バッチ正規化は、悪い重み初期化の影響を軽減し、深いネットワークのトレーニングを容易にします。
より良い汎化性能
バッチ正規化による正則化効果により、過学習を防止し、未知のデータに対するモデルの汎化性能を改善することができます。
ハイパーパラメータの簡素化
バッチ正規化はトレーニングを安定化させるため、緻密なハイパーパラメータのチューニングが必要な場合が少なくなり、時間と計算リソースを節約することができます。

バッチ正規化は、画像分類、物体検出、セマンティックセグメンテーションなどのコンピュータビジョンタスクにおいて、多数の最先端モデルの性能向上に貢献してきました。さらに、バッチ正規化は、層正規化、インスタンス正規化、グループ正規化などの他の正規化手法の開発にも影響を与え、自然言語処理や強化学習などの様々な分野で応用されています。

背景と理論

共変量シフト

共変量シフトとは、トレーニングプロセス中に入力特徴の分布が変化することを指します。この現象は、前の層のパラメータが更新されるたびに、各層への入力の分布が変化する内部共変量シフトという問題を引き起こすことがあります。内部共変量シフトは、安定性を維持するために低い学習率と注意深い初期化が必要であり、トレーニングを遅くする可能性があります。

バッチ正規化は、各層への入力分布がトレーニング中に一貫していることを保証することで、内部共変量シフトの問題に対処します。これは、各層のアクティベーションを正規化することで達成され、学習プロセスを安定化し、より高い学習率を使用することを可能にします。

バッチ正規化アルゴリズム

バッチ正規化は、アクティベーション関数が適用される前の各層のアクティベーションに適用されます。アルゴリズムは次の手順に分解できます。

各特徴量について、ミニバッチ内のアクティベーションの平均値と分散を計算
計算された平均値と分散を使用して、アクティベーションを正規化
学習可能なパラメータ（ $\gamma$ と $\beta$ ）を使用して、正規化されたアクティベーションをスケーリングおよびシフト。これらのパラメータはトレーニング中に更新される。

数学的には、正規化の手順は次のように表されます。

x_\text{normalized} = \frac{x - \mu(x)}{\sqrt{\sigma^2(x) + \epsilon}}

ここで、 $x$ は入力アクティベーションを表し、 $\mu(x)$ および $\sigma^2(x)$ はミニバッチ内のアクティベーションの平均値と分散を表し、 $\epsilon$ は数値安定性のために追加される小さな定数です。

スケーリングおよびシフトの手順は、次のように表されます。

y = \gamma \cdot x_\text{normalized} + \beta

ここで、 $\gamma$ と $\beta$ は学習可能なパラメータであり、 $y$ はバッチ正規化層の出力を表します。

主要なパラメータとハイパーパラメータ

バッチ正規化には、動作に影響を与えるいくつかの主要なパラメータとハイパーパラメータがあります。

ミニバッチサイズ
正規化に使用されるミニバッチのサイズは、平均値と分散の推定に影響します。大きなバッチサイズはより正確な推定を提供しますが、より多くのメモリと計算リソースを必要とします。小さなバッチサイズは正規化プロセスにノイズを導入する可能性がありますが、有益な正則化効果を持つ場合があります。
モメンタム
バッチ正規化は、トレーニング中に平均値と分散の移動平均を維持し、テスト時に正規化に使用します。モメンタムパラメータは、現在のミニバッチの統計量が移動平均に与える重みを決定します。モメンタムの典型的な値は、0.9から0.99の範囲です。
$\epsilon$
$\epsilon$ パラメータは、数値安定性のために分散に追加される小さな定数です。 $\epsilon$ の典型的な値は、1e-5から1e-8の範囲です。
学習可能なパラメータ（ $\gamma$ および $\beta$ ）
$\gamma$ および $\beta$ パラメータは、正規化されたアクティベーションをスケーリングおよびシフトするために使用されます。これらのパラメータはトレーニング中に学習され、モデルが多様な入力分布を表現できるようにします。

バッチ正規化ありとなしのモデルの比較

この章では、バッチ正規化ありとなしのディープラーニングモデルの性能を比較します。人気のあるMNISTデータセットを使用して、手書き数字を分類する単純なフィードフォワードニューラルネットワークをトレーニングします。最後に、Matplotlibを使用して両方のモデルの学習曲線をプロットします。

まず、必要なライブラリをインポートし、データセットをロードします。

python

import numpy as np
import matplotlib.pyplot as plt
import tensorflow as tf
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, BatchNormalization, Activation
from tensorflow.keras.optimizers import Adam

(x_train, y_train), (x_test, y_test) = mnist.load_data()

x_train = x_train.reshape(60000, 784).astype('float32') / 255
x_test = x_test.reshape(10000, 784).astype('float32') / 255
y_train = tf.keras.utils.to_categorical(y_train, 10)
y_test = tf.keras.utils.to_categorical(y_test, 10)

次に、オプションのバッチ正規化層を備えたモデルを作成する関数を定義します。

python

def create_model(use_batchnorm):
    model = Sequential()
    model.add(Dense(128, input_shape=(784,)))
    if use_batchnorm:
        model.add(BatchNormalization())
    model.add(Activation('relu'))
    model.add(Dense(64))
    if use_batchnorm:
        model.add(BatchNormalization())
    model.add(Activation('relu'))
    model.add(Dense(10, activation='softmax'))
    return model

その後、バッチ正規化ありとなしの2つのモデルを作成してトレーニングします。

python

model_without_bn = create_model(use_batchnorm=False)
model_without_bn.compile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy'])
history_without_bn = model_without_bn.fit(x_train, y_train, batch_size=128, epochs=20, verbose=1, validation_data=(x_test, y_test))

model_with_bn = create_model(use_batchnorm=True)
model_with_bn.compile(loss='categorical_crossentropy', optimizer=Adam(), metrics=['accuracy'])
history_with_bn = model_with_bn.fit(x_train, y_train, batch_size=128, epochs=20, verbose=1, validation_data=(x_test, y_test))

最後に、Matplotlibを使用して学習曲線をプロットします。

python

plt.style.use('ggplot')
plt.figure(figsize=(10, 6))

plt.plot(history_without_bn.history['accuracy'], linestyle='-', label='Training (No BN)')
plt.plot(history_without_bn.history['val_accuracy'], linestyle='--', label='Validation (No BN)')
plt.plot(history_with_bn.history['accuracy'], linestyle='-', label='Training (With BN)')
plt.plot(history_with_bn.history['val_accuracy'], linestyle='--', label='Validation (With BN)')

plt.title('Learning Curves: With and Without Batch Normalization')
plt.xlabel('Epoch')
plt.ylabel('Accuracy')
plt.legend()

plt.show()

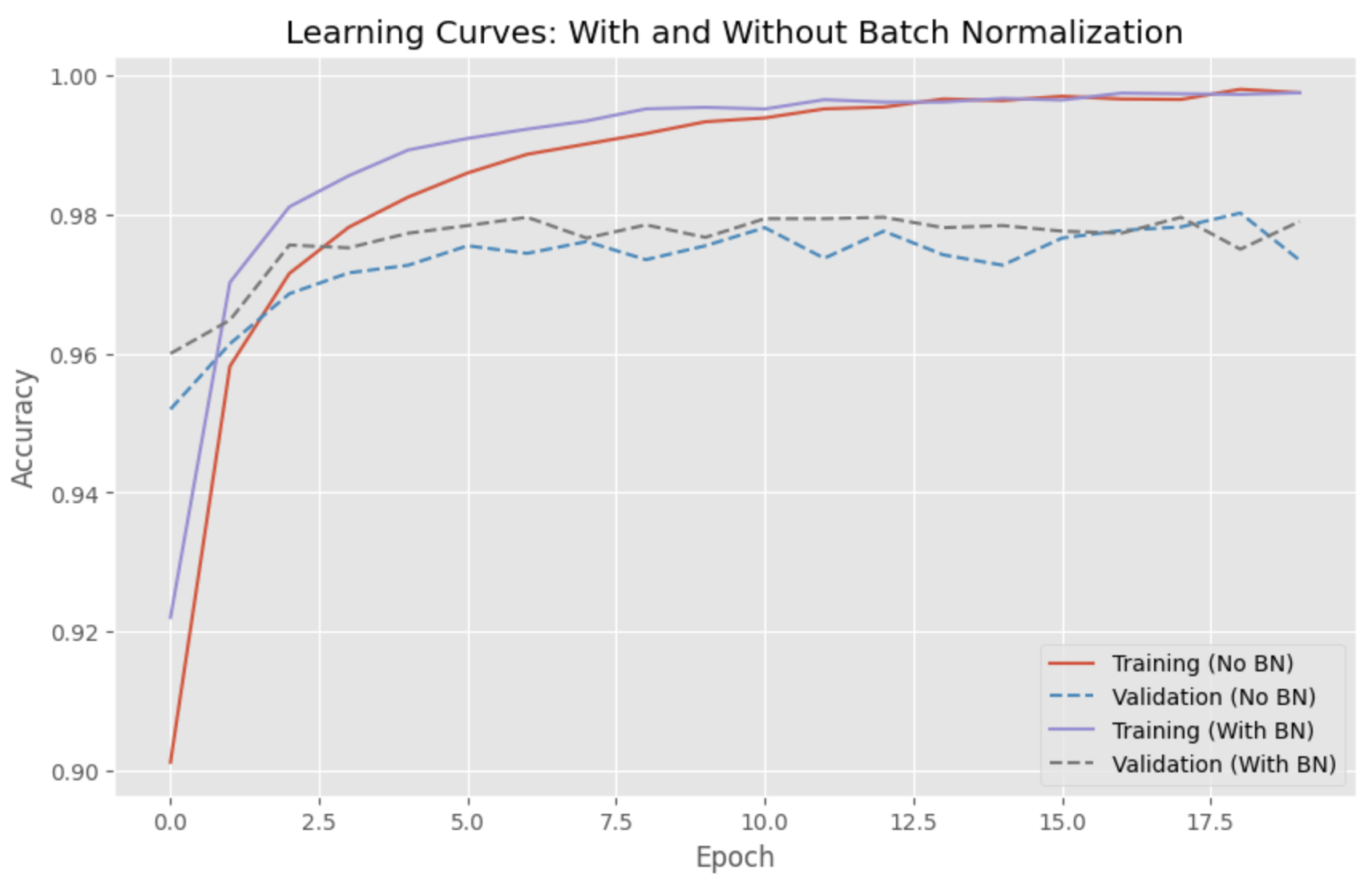
Learning curve

学習曲線は、バッチ正規化ありのモデルがより速く収束し、バッチ正規化なしのモデルよりも高い検証精度を達成していることを示しています。

バッチ正規化

バッチ正規化とは

バッチ正規化の重要性

背景と理論

共変量シフト

バッチ正規化アルゴリズム

主要なパラメータとハイパーパラメータ

バッチ正規化ありとなしのモデルの比較

参考

勾配消失問題

ディープラーニングにおける重みの初期化

Ryusei Kakujo