はじめに

隠れ層のアクティベーション分布は、ニューラルネットワークの学習プロセスにおいて重要な役割を果たします。よく分布されたアクティベーションは、ネットワークがより複雑な機能を学習し、新しい、未知のデータに対して一般化することができます。隠れ層内のアクティベーション分布を分析することで、研究者や実践者は潜在的な問題を診断し、パフォーマンスを最適化し、モデル全体の効率を改善することができます。

アクティベーション分布の分析方法

隠れ層のアクティベーション分布をよりよく理解するために、様々な可視化と分析技術が用いられます。

• ヒストグラム
  ヒストグラムは、アクティベーション分布を可視化するための一般的な方法です。特定の値範囲内のアクティベーションの頻度をプロットすることにより、分布の形状や広がりについて洞察を提供し、バニッシングまたは爆発的な勾配などの問題を特定するのに役立ちます。

• 密度プロット
  密度プロットは、アクティベーション分布の滑らかで連続的な表現を提供します。これにより、分布の基本的な構造を明らかにし、アクティベーション値の多様性の欠如やデッドニューロンなどの潜在的な問題を特定することができます。

• 累積分布関数（CDF）プロット
  CDFプロットは、アクティベーション値の累積確率を視覚化します。CDFプロットの傾きを分析することで、アクティベーションが集中したりまばらな領域を特定し、分布を改善するための戦略を考えることができます。

アクティベーション分布の共通問題

アクティベーションの分布に関する問題は、ニューラルネットワークの学習プロセスに否定的な影響を与えることがあります。

• 勾配消失
  勾配消失は、勾配値が非常に小さくなり、ネットワークの重みが非常に遅くまたは全く更新されなくなる問題です。この問題は、シグモイドや双曲線正接などの出力値の範囲が限定された活性化関数を使用する場合に頻繁に発生します。

• 勾配爆発
  勾配爆発は、勾配値が大きすぎるために、学習プロセスに不安定性が生じ、モデルが発散する可能性がある問題です。この問題は、深層ネットワークでより一般的であり、適切な重み初期化、勾配クリッピング、または正規化技術を使用することで緩和できます。

• デッドニューロン
  デッドニューロンとは、入力に関係なく、隠れ層の特定のニューロンが一定の値を出力し続ける状況を指します。ReLU関数のように勾配がゼロの領域を持つ活性化関数を使用する場合に発生することがあります。デッドニューロンは、ネットワークの出力に有意な貢献をしないため、学習プロセスを妨げることがあります。

アクティベーション分布の最適化

上記の問題に対処し、隠れ層のアクティベーション分布を最適化するために、いくつかの技術が適用されます。

• 適切な活性化関数の選択
  出力値と勾配の範囲が広い活性化関数を使用することで、勾配消失または勾配爆発を防ぐことができます。例えば、ReLUおよびその派生関数は、広い入力範囲で非ゼロの勾配を維持する能力から人気があります。

• 適応学習率
  AdamやRMSPropなどの適応学習率アルゴリズムを使用することで、各重みに対して学習率を個別に調整することで、勾配消失または勾配爆発の影響を緩和することができます。

• 重みの初期化技術
  XavierやHe初期化などの適切な重み初期化は、初期の重みがアクティベーションをあまり小さくまたは大きくしないようにすることで、勾配消失または勾配爆発を防ぐのに役立ちます。

• 正則化技術
  L1またはL2正則化などの正則化技術を適用することで、スパーシティを促進したり、重みが大きすぎることを防いだりすることで、デッドニューロンの影響を緩和することができます。

• 正規化技術
  バッチ正規化や層正規化などの正規化技術を使用することで、トレーニング中に各隠れ層の入力を正規化することで、学習プロセスを安定化し、アクティベーション分布を改善することができます。これにより、より速い収束と改善された汎化性能が得られます。

• 勾配クリッピング
  勾配クリッピングは、バックプロパゲーション中の勾配の大きさを制限する技術です。勾配が大きすぎることを防ぐことで、勾配爆発の影響を緩和し、学習プロセスの安定性を向上させることができます。

• スキップ接続
  Residual Networks（ResNet）などのアーキテクチャで使用されるスキップ接続は、特定の層をバイパスすることで、勾配がより簡単にネットワークを流れるようにすることができます。これは、特により深いネットワークで勾配消失問題を軽減するのに役立ちます。

アクティベーション分布を改善する技術

この章では、隠れ層のアクティベーション分布を改善するために適用できるさまざまな技術について詳しく説明します。これにより、ニューラルネットワークのパフォーマンスと効率が向上します。

重みの初期化

ニューラルネットワークの重みの初期化は、アクティベーション分布に大きな影響を与えます。適切な重みの初期化により、勾配消失または勾配爆発を防ぎ、より速い収束を促進することができます。いくつかの一般的な重みの初期化方法は次のとおりです。

• Xavier（Glorot）初期化
  この方法は、レイヤー内の入力ユニット数と出力ユニット数に基づいて初期重みを設定します。シグモイドや双曲線正接の活性化関数と併用する場合に特に効果的です。

• He初期化
  Xavier初期化に似ていますが、He初期化はReLUとその派生関数に特化しています。入力ユニット数と出力ユニット数を考慮しています。

• LeCun初期化
  この方法は、シグモイドや双曲線正接の活性化関数に適した初期化方法で、レイヤー内の入力ユニット数のみを考慮します。

バッチ正規化

バッチ正規化は、アクティベーションをスケーリングしてシフトすることで、トレーニング中の各隠れ層の入力を正規化する技術です。バッチ正規化は、勾配消失または勾配爆発を解決し、より均等に分布したアクティベーションを促進するために特に有用です。

層正規化

層正規化は、可変長シーケンスや小規模なバッチサイズを扱う場合に特に有用なバッチ正規化の代替手段です。バッチ全体で入力を正規化するのではなく、各隠れ層内の特徴量ごとに入力を正規化します。これにより、より安定したアクティベーション分布と学習ダイナミクスが得られることがあります。

正則化

正則化技術を使用することで、スパーシティを促進したり、重みが大きすぎることを防いだりすることで、アクティベーション分布を改善することができます。一般的な正則化方法は次のとおりです。

• L1正則化
  L1正則化は、重みの絶対値に比例したL1ペナルティを損失関数に加えます。これにより、重み行列のスパーシティが促進され、デッドニューロンの影響を緩和することができます。

• L2正則化
  L2正則化は、重みの2乗に比例したL2ペナルティを損失関数に加えます。これにより、重みが大きすぎることを防ぎ、勾配消失または勾配爆発に関連する問題を軽減することができます。

• ドロップアウト
  ドロップアウトは、トレーニング中にランダムなサブセットのニューロンを一時的に無効化する正則化技術です。これにより、モデルが単一のニューロンに過剰に依存することを防ぎ、より均等に分布したアクティベーションを促進することができます。

隠れ層のアクティベーション分布の可視化

この章では、アヤメデータセットを使用して、隠れ層のアクティベーション分布を可視化する方法を説明します。アヤメデータセットは、アヤメの花の3種類（アイリス・セトサ、アイリス・バーシクラー、アイリス・ヴァージニカ）それぞれから50サンプルを含む公開データセットで、計150サンプルが含まれています。このデータセットで単純なフィードフォワードニューラルネットワーク（FFNN）をトレーニングし、アクティベーションのヒストグラムを描画します。

データセットとモデル概要

アヤメデータセットは、3つの種類のアヤメの花（アイリス・セトサ、アイリス・バーシクラー、アイリス・ヴァージニカ）それぞれから50サンプルを含む計150サンプルで構成されています。各サンプルには、がくの長さ、がくの幅、花弁の長さ、花弁の幅の4つの特徴量と、種を示すラベルがあります。

FFNNモデルは、次のアーキテクチャを持ちます。

1. 4つの入力ノードを持つ入力層。
2. 64のユニットとReLUアクティベーションを持つ完全接続（密な）層
3. 32のユニットとReLUアクティベーションを持つ完全接続（密な）層
4. 16のユニットとReLUアクティベーションを持つ完全接続（密な）層
5. 3つのユニットとソフトマックスアクティベーションを持つ出力層

前処理とトレーニング

次のPythonコードを使用してデータを前処理し、モデルをトレーニングします。

import torch
import torch.nn as nn
import torch.optim as optim
from torch.autograd import Variable
import torch.nn.functional as F
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.preprocessing import OneHotEncoder

# Load and preprocess the data
iris = datasets.load_iris()
X = iris.data
y = iris.target

# Normalize the features
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# One-hot encode the target labels
encoder = OneHotEncoder()
y_onehot = encoder.fit_transform(y.reshape(-1, 1)).toarray()

# Split the data into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(
    X_scaled, y_onehot, test_size=0.2, random_state=42)

# Convert the data to PyTorch tensors
X_train = Variable(torch.Tensor(X_train).float())
X_test = Variable(torch.Tensor(X_test).float())
y_train = Variable(torch.Tensor(y_train).float())
y_test = Variable(torch.Tensor(y_test).float())

# Define the model
class Iris_FFNN(nn.Module):
    def __init__(self):
        super(Iris_FFNN, self).__init__()
        self.fc1 = nn.Linear(4, 64)
        self.fc2 = nn.Linear(64, 32)
        self.fc3 = nn.Linear(32, 16)
        self.fc4 = nn.Linear(16, 3)

    def forward(self, x):
        x = F.relu(self.fc1(x))
        x = F.relu(self.fc2(x))
        x = F.relu(self.fc3(x))
        x = self.fc4(x)
        return x

model = Iris_FFNN()

# Set loss function and optimizer
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(), lr=0.001)

# Train the model
num_epochs = 500
for epoch in range(num_epochs):
    optimizer.zero_grad()
    outputs = model(X_train)
    loss = criterion(outputs, y_train)
    loss.backward()
    optimizer.step()
    if (epoch + 1) % 50 == 0:
        print(f'Epoch [{epoch+1}/{num_epochs}], Loss: {loss.item()}')

print('Finished training')

アクティベーション分布の可視化

隠れ層のアクティベーション分布を可視化するために、層1、層2、層3のアクティベーションのヒストグラムを描画します。これを行うには、まず隠れ層からアクティベーションを抽出する関数を作成します。

def get_activations(model, layer_indices, input_data):
    activations = []

    for index in layer_indices:
        activation_model = nn.Sequential(*(list(model.children())[:index+1]))
        activation = activation_model(input_data)
        activations.append(activation)

    return activations

次に、トレーニング済みのモデルにテストサンプルのバッチを渡し、隠れ層からのアクティベーションを収集します。

# Get the activations from the hidden layers
hidden_layer_indices = [0, 1, 2]
activations = get_activations(model, hidden_layer_indices, X_test)

最後に、Matplotlibを使用してこれらのアクティベーションのヒストグラムをプロットします。

import matplotlib.pyplot as plt

plt.style.use('ggplot')

def plot_activation_histograms(activations, layer_indices):
    num_layers = len(activations)

    fig, axes = plt.subplots(1, num_layers, figsize=(15, 5))

    for i, activation in enumerate(activations):
        layer_index = layer_indices[i]
        axes[i].hist(activation.detach().numpy().flatten(), bins=50, orientation='vertical', alpha=0.5)
        axes[i].set_title(f'Layer {layer_index + 1} Activations')
        axes[i].set_xlabel('Activation Value')

    axes[0].set_ylabel('Frequency')
    plt.tight_layout()
    plt.show()

plot_activation_histograms(activations, hidden_layer_indices)

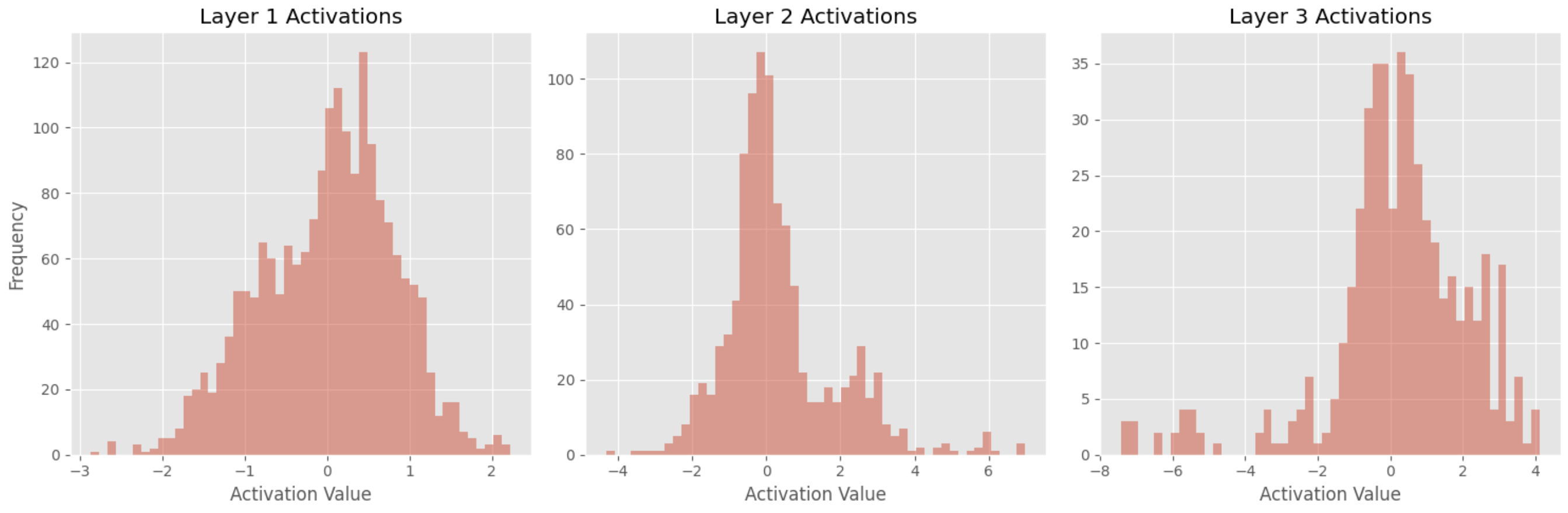
結果の解釈

ヒストグラムをプロットした後、アクティベーション分布を分析し、いくつかの結論を導き出すことができます。

• 最頻値が0
  3つの層全てでもっとも頻繁なアクティベーション値が0であることから、ネットワークの多くのニューロンが入力データによって活性化されていないことが示唆されます。これは、ReLUアクティベーション関数を使用しているため、全ての負の入力値に対して0を出力することが原因かもしれません。

• 尖度の増加
  層1から層3にかけての尖度の増加は、ニューラルネットワークの深層部に進むにつれて、アクティベーション値の分布がより尖った形状になり、テールが重くなることを示唆しています。これは、深い層のニューロンが入力データの特定の特徴に選択的に反応し、他の特徴を無視している可能性があり、これはデータのより複雑な表現を学習していることを示すサインかもしれません。

• より広い範囲
  層1から層3にかけてアクティベーション値の範囲が広がっていることから、深層部のニューロンが入力データの変動により敏感であることが示唆されます。これは、ネットワークがデータからより細かい特徴を抽出することを学習しているサインかもしれません。