巡回セールスマン問題（TSP）とは

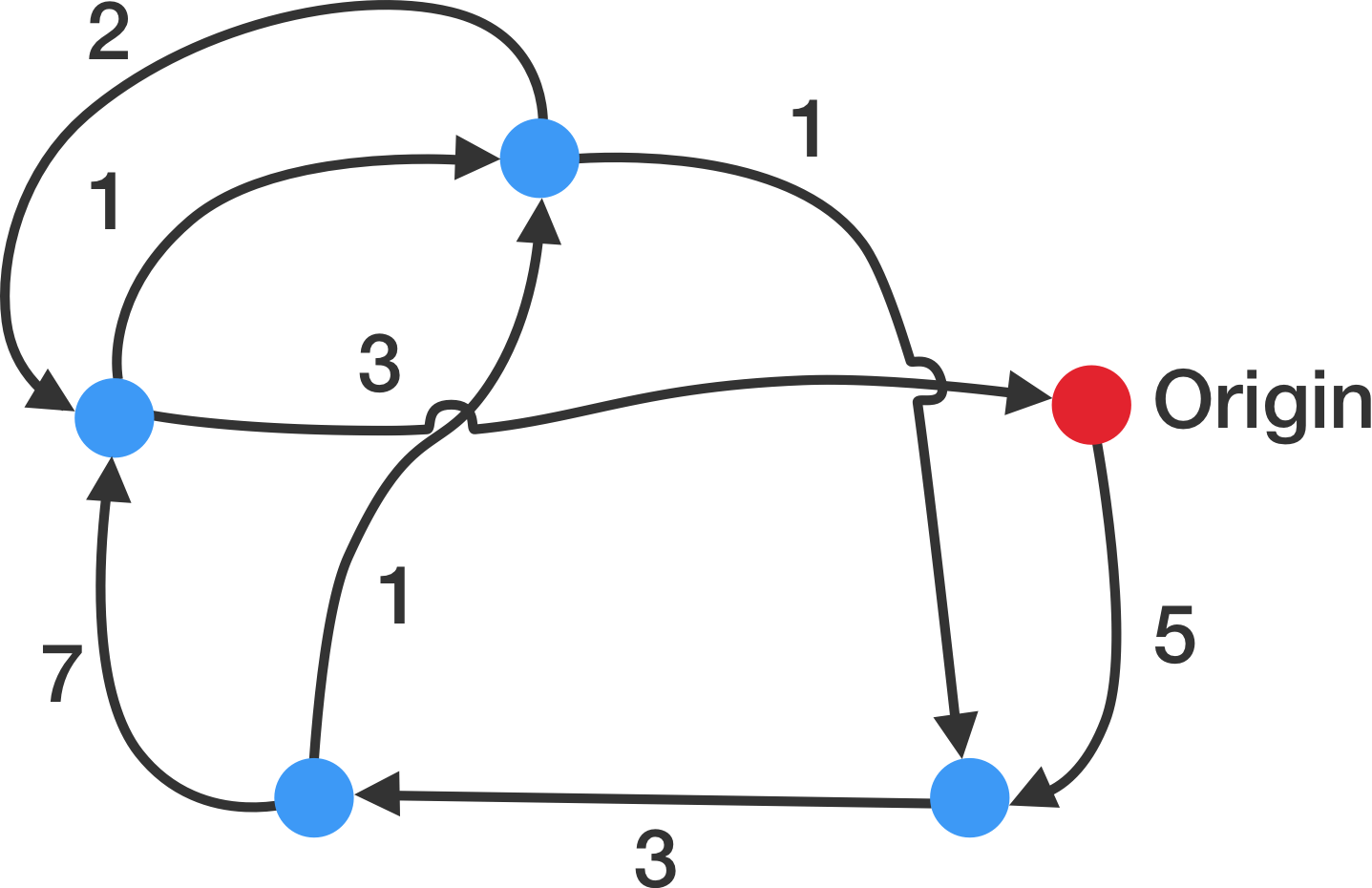
巡回セールスマン問題（Traveling Salesman Problem, TSP）は、コンピュータ科学やオペレーションリサーチの分野における最適化に焦点を当てた古典的なアルゴリズム問題です。TSPの基本的な形式では、セールスマンが複数の都市を訪れる必要があり、セールスマンが各都市を一度だけ訪れて出発地に戻るための最短経路を見つけることが求められます。

この問題は理解するのは簡単ですが、都市（または「ノード」と呼ばれる）の数が増えると驚くほど複雑な解決が必要とされます。数学的な観点からは、有限の解の集合から最適な解を見つけるという組合せ最適化の問題となります。

Traveling Salesperson Problem

問題の複雑さ

コンピュータ科学において、アルゴリズムの複雑さとは、問題を解くためにアルゴリズムが必要とする時間や空間などの計算リソースの量を測る指標です。TSPの複雑さは、セールスマンが訪れる都市の数に直接関連しています。

TSPの複雑さを評価する際には、時間複雑性（問題を解くために必要な計算処理時間）と空間複雑性（必要なメモリスペースの量）の両方を考慮する必要があります。

例えば、全ての可能な経路を計算して比較する「力まかせな」アプローチは、階乗時間の複雑性（O(n!)）を持ちます。つまり、問題を解くためにかかる時間は都市の数とともに指数関数的に増加し、大きな問題に対してはこのアプローチは実用的ではありません。

P vs NP

計算理論の分野では、問題はしばしばその固有の難しさを反映するためにカテゴリに分類されます。その中にはP（素早く解ける問題）とNP（解が素早く確認できる問題）というカテゴリがあります。PとNPが等しいかどうかという問題は、コンピュータ科学におけるもっとも基本的な未解決問題の一つです。

TSPはNP困難な問題として分類されています。つまり、NPの中でもっとも難しい問題と同等以上の難しさを持つ問題です。もしTSPを素早く（「多項式時間」で）解くアルゴリズムが見つかれば、それはNPの他の問題を解くためにも使用でき、実質的にP=NPを証明することになります。しかし、広範な研究が行われているにもかかわらず、そのようなアルゴリズムは見つかっておらず、多くのコンピュータ科学者はそのようなアルゴリズムは存在しないと考えています。

TSPのバリエーション

対称TSP

対称TSPでは、都市Aから都市Bへの距離は都市Bから都市Aへの距離と同じです。これはもっとも一般的な問題の形式であり、多くの人々がよく知っているものです。道路網など、多くの現実世界のシナリオは対称TSPとして表現できます。

非対称TSP

非対称TSPでは、都市Aから都市Bへの距離は必ずしも都市Bから都市Aへの距離と同じではありません。このバリエーションは、航空旅行のように全ての空港のペア間で直行便が利用できない場合や、道路の種類や一方通行が関わる物流のシナリオなど、双方向の移動が行われない場合に適用されます。

その他のバリエーション

TSPには他にもさまざまなバリエーションが存在し、それぞれ独自の特徴と課題を持っています。これには次のものが含まれます。

• 複数TSP (mTSP)
  このバリエーションでは、複数のセールスマンが利用可能であり、全てのセールスマンが移動する総距離を最小化することが目標となります。

• 時間依存TSP
  時間依存TSPでは、都市間の移動時間が出発時刻に依存します。このバリエーションは、一日の中で交通渋滞が異なる場面でよく使用されます。

• 運搬経路問題（VRP）
  これはTSPの一般化された形式であり、複数の車両が最適に経路を設定する必要があります。

解決手法

巡回セールスマン問題に取り組む際には、一般的に正確なアルゴリズムとヒューリスティックアルゴリズムの2つの大きなクラスの手法が使用されます。

正確なアルゴリズムは問題に正確で最適な解を提供するように設計されています。これらの手法は最短経路を保証します。しかし、TSPの計算上の複雑さのため、正確なアルゴリズムは計算上高コストであり、問題のサイズが小さい場合にのみ実用的です。

一方、ヒューリスティックアルゴリズムは効率を重視した手法です。これらの手法は近似解を提供し、正確な解が時間や計算リソースの制約により実現不可能な大規模な問題に対して特に有用です。ヒューリスティックは最短経路を保証するわけではありませんが、しばしば最適解に「十分近い」解を提供します。

正確なアルゴリズム

全探索（ブルートフォース法）

TSPへのもっとも基本的な解法は、全探索です。このアルゴリズムは全ての可能な経路のコストを計算し、もっとも安価なものを選択します。このアプローチは最適解を保証しますが、都市の数が増えると階乗時間の複雑性により計算上の制約が生じ、実用的ではありません。

ヘルド・カープ法

ヘルド・カープ法は、全探索法に比べてTSPを解くための時間複雑性を大幅に低下させる動的計画法の手法です。この手法は各都市を訪れる最短経路を段階的に構築し、冗長な計算を避けるために以前に計算された結果を活用します。しかし、依然として指数時間の複雑性を持ち、比較的小さな問題に対してのみ実用的に使用されます。

ヒューリスティックアルゴリズム

最近傍法

最近傍法は、セールスマンがまだ訪れていない都市の中でもっとも近い都市に移動するというシンプルなヒューリスティックです。この手法は最適解を保証しませんが、計算が迅速であり、実用上十分な解を提供することが多いです。

焼きなまし法

焼きなまし法は、確率的な手法であり、探索の初期段階ではより最適でない解を受け入れることで局所的な最小値に陥ることを回避します。時間の経過とともに探索は徐々により焦点を絞り、冶金学での焼きなまし過程を模倣します。

遺伝的アルゴリズム

遺伝的アルゴリズムは、自然選択の過程に着想を得たヒューリスティックの一種です。TSPの解は、個体として扱われ、世代を重ねるごとに突然変異、交叉（再結合）、選択操作によってより良い解に進化します。この手法は高度に並列化が可能であり、大規模な問題に対して高品質な解を提供することができますが、最適解を保証するわけではありません。

TSP解決の現代的な進展

量子コンピューティング

量子コンピューティングは、TSPのようなNP困難な問題を解決するための新たなフロンティアを開いています。量子コンピュータは、重ね合わせという概念を利用して複数の解を同時に探索することができます。このアプローチは、特に問題の大規模なインスタンスに対してTSPを解決するために必要な時間を劇的に短縮する可能性があります。

現在、量子コンピューティングの分野はまだ初期段階にあり、TSPを解決するための量子アルゴリズムの開発は積極的に行われています。初期の結果は有望であり、技術の成熟に伴い、古典的なコンピュータよりも効率的に大規模なTSPのインスタンスを解決できる可能性があります。

機械学習アプローチ

機械学習は、TSPの解決に応用されている別の領域です。機械学習アルゴリズムは、問題の複数のインスタンスをトレーニングデータとして使用してTSPの近似解を学習することができます。

一つの注目すべきアプローチは、強化学習を使用するものです。エージェントは環境内で行動を取り、報酬の形でフィードバックを受けながらTSPを解く方法を学習します。エージェントの目標は、合計報酬を最大化するポリシーを学習することであり、TSPの場合はツアーの総距離を最小化することに相当します。

別のアプローチでは、ニューラルネットワークを使用してTSPを解くためのヒューリスティックを学習します。これらの「ニューラルヒューリスティック」は、問題のインスタンスとその解のデータセットを用いて学習し、問題の現在の状態に基づいて次に訪れる都市を予測することを学習します。

これらの機械学習アプローチは最適解を保証するわけではありませんが、正確なアルゴリズムに比べて短時間で高品質な解を提供できるため、より大規模なTSPのインスタンスの解決に向けた有望な手段となっています。