2022-12-08

計算複雑性理論

計算複雑性理論とは

計算複雑性理論は、与えられた計算問題を解決するために必要な計算資源を研究するコンピュータ科学の分野です。これらの資源には時間（問題を解決するのにかかるステップ数）や空間（問題を解決するために必要なメモリ量）が含まれますが、他の複雑性の尺度も考慮されることがあります。

計算複雑性理論の主な目的は、問題をその固有の難しさに基づいて分類することです。これを行うために、複雑性クラスを定義します。これは、同様の計算資源の量を使用して解決できる問題の集合です。重要な複雑性クラスには、P、NPなどがあります。

計算複雑性理論の中心的な側面の一つは、解けない問題、つまり効率的な解法が存在しない問題の研究です。これらおよびその他の問題の探求を通じて、計算複雑性理論はコンピュータが何ができるか、できないかの限界を明らかにし、アルゴリズムの設計、ソフトウェアの開発、コンピューティング技術の進歩において重要な洞察を提供します。

時間計算量

時間計算量は、計算複雑性理論の概念の一つであり、アルゴリズムの実行にかかる計算時間を、プログラムの入力サイズの関数として表します。アルゴリズムの効率を評価する上で、時間計算量の理解は非常に重要です。

ビッグオー記法

ビッグオー記法は、アルゴリズムの時間計算量の上界、つまり最悪の場合のシナリオを表現するために使用される数学的な記法です。これは、アルゴリズムの実行時間が入力のサイズとともにどのように増加するかを示します。例えば、時間計算量が $O(n)$ のアルゴリズムは、入力サイズと線形に増加します。

O(1): 定数時間の複雑さ

アルゴリズムが入力のサイズに依存しない場合、定数時間の複雑さを持つと言います。入力がどれだけ大きくても、計算時間は一定です。

例

配列内の特定の要素へのアクセス。配列がどれほど大きくても、インデックスが分かっていれば、配列の要素を読むためには1つのステップしか必要ありません。

O(n): 線形時間の複雑さ

アルゴリズムが実行時間が入力データのサイズとほぼ線形に増加する場合、線形時間の複雑さを持つと言います。

例

特定の値を見つけるために配列を繰り返し検索するシンプルな検索関数は、最悪の場合において、全ての要素を1回ずつ見る必要があるため、 $O(n)$ の時間複雑さを持ちます。

O(log n): 対数時間の複雑さ

対数時間の複雑さは、問題のサイズを各ステップで分数に減らしていくアルゴリズムに関連しています。

例

2分探索は、対数時間の複雑さである $O(\log n)$ を持つアルゴリズムです。2分探索アルゴリズムの各ステップでは、検索対象の要素数が半分になるため、目標を見つけるのに対数的に少ないステップが必要です。

O(n^2): 二次時間の複雑さ

アルゴリズムが各要素に対して処理を行い、その処理が要素のループを含む場合、二次時間の複雑さを持つと言います。

例

バブルソートは、 $O(n^2)$ の複雑さを持つ典型的な例です。バブルソートでは、配列内の各要素ごとに他の全ての要素と比較を行います。

O(2^n): 指数時間の複雑さ

指数時間の複雑さは、入力データセットの要素の追加ごとに成長が2倍になる場合に発生します。 $O(2^n)$ の関数の成長曲線は指数的であり、最初は非常に緩やかであり、急速に上昇します。

例

$O(2^n)$ の複雑さの典型的な例は、フィボナッチ数の再帰的な計算です。素朴な再帰アルゴリズムでは、重複した計算が過剰に行われ、入力サイズの増加ごとに作業量が2倍になります。

空間計算量

空間計算量は、計算複雑性理論のもう一つの重要な概念です。これは、アルゴリズムが入力のサイズに対して必要とするメモリスペースの量を表します。時間計算量と同様に、アルゴリズムの空間計算量を理解することは、特にメモリ制約のある環境で効率を評価する上で重要です。

複雑性クラス

複雑性クラスは、同様のリソースに基づいた特徴を共有する計算問題をグループ化する方法です。これらの特徴は通常、問題の解決に必要な時間や空間と関連しています。

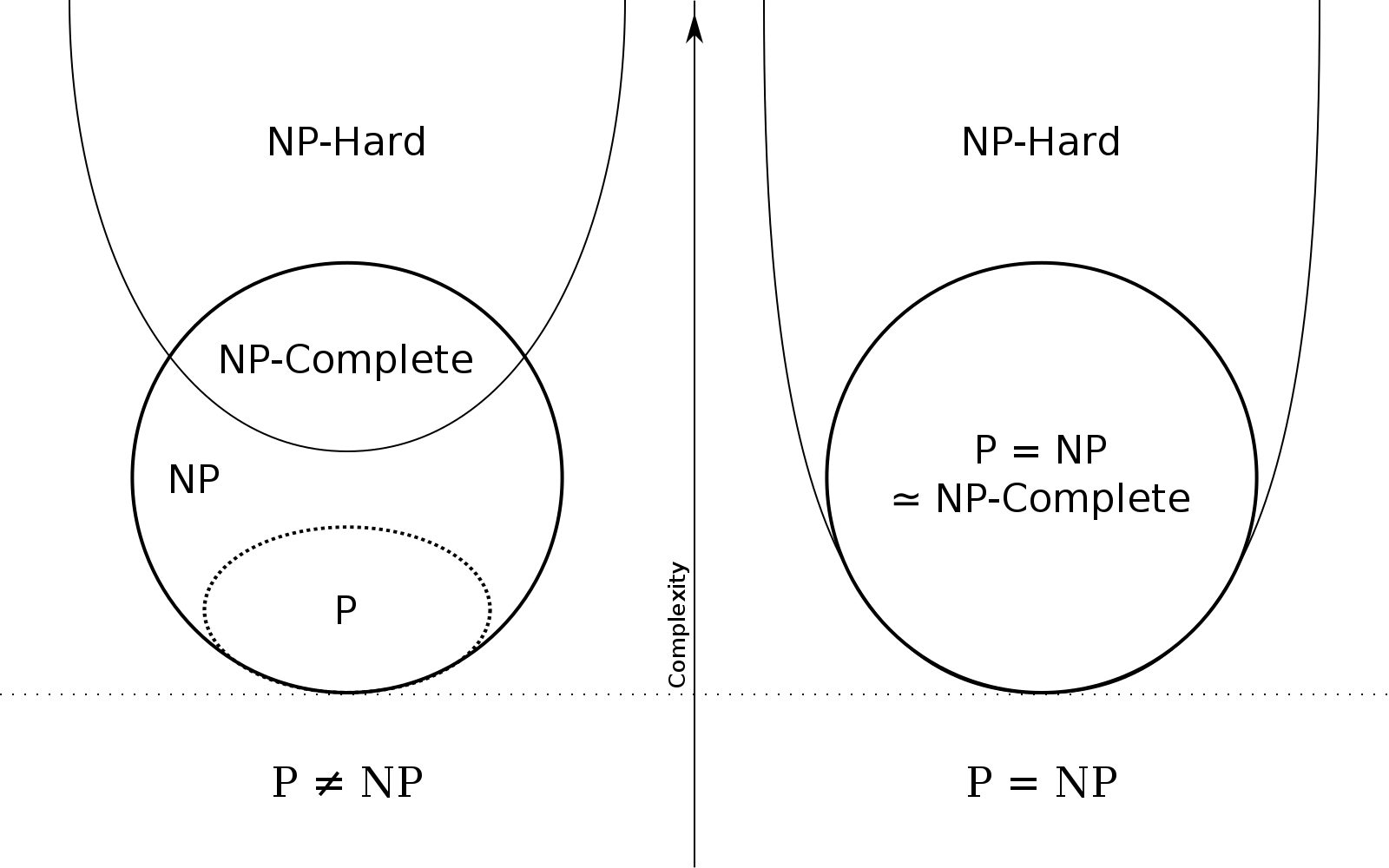
Complexity classes
File:P np np-complete np-hard.svg

クラスP

クラスP（多項式時間）は、決定性チューリングマシンが多項式時間で解ける判定問題の集合です。ビッグオー記法では、解く問題の時間計算量が $O(p(n))$ となるような多項式 $p(n)$ が存在します。

例えば、入力のサイズを表す $n$ に対して $O(n^2)$ の時間で解ける問題はクラスPに属します。つまり、入力のサイズが大きくなるにつれて問題の解決にかかる時間が二次的に増加します。

クラスNP

クラスNPには、解が与えられた場合に決定性チューリングマシンで多項式時間で検証できる問題が含まれます。これは問題が多項式時間で解けることを意味するわけではありません。むしろ、誰かが解の候補を提供した場合に、その解の正しさを多項式時間でチェックできることを意味します。

例えば、ある問題の解候補の正しさを $O(n^3)$ の時間で検証できる場合、その問題はクラスNPに属します。

NP完全問題

NP完全は、NPに属する問題を、多項式時間で帰着することができる問題の集合を表します。

NP完全クラスには2つの主要な特性があります。

問題自体がNPに属していること。つまり、問題の「証明」または問題の解の候補を与えられた場合、その解の正しさを多項式時間で検証できることを意味します。
NPの任意の問題を多項式時間で帰着できること。言い換えれば、この問題に対して多項式時間の解法が存在するとすれば、NPの全ての問題を多項式時間で解くことができます。