マルサスモデルとは

マルサスモデルは、利用可能な資源に関連して人口の成長を示す人口統計モデルです。このモデルは、18世紀末から19世紀初頭にかけてのイギリスの聖職者兼学者、トマス・ロバート・マルサスによって開発されました。マルサスモデルの中心的なアイデアは、人口が指数関数的に成長する一方で、食料などの資源の成長が算術的な速度で進むということです。マルサスによれば、成長率のこの違いは最終的に人口過剰を引き起こし、資源の不足を招き、飢饉、疫病、その他の災害的な出来事による人口の崩壊につながるとされています。

マルサスの成長方程式の基本

マルサスモデルは、人口の成長率が現在の人口の大きさに比例するという概念に基づいています。数学的には、これは微分方程式によって表されます。

ここで、Pは時刻tにおける人口の大きさを表し、\frac{dP}{dt}は時間に関する人口の変化率を示し、rは人口の固有成長率です。

この微分方程式の解は指数関数です。

ここで、P(0)は時刻0における人口の大きさを表し、eはネイピア数（約2.71828）です。

仮定と単純化

基本的なマルサス成長方程式にはいくつかの重要な仮定があります。

• 一定の成長率
  固有成長率（r）は一定であると仮定されています。つまり、出生と死亡の割合は時間の経過とともに変化しないということです。

• 無制限の資源
  このモデルでは、人口成長に必要な資源に制限がないと仮定されています。現実には、食料、空間、その他の資源などが人口成長を制限する要因となります。

• 閉鎖人口
  このモデルでは、移民や移住を考慮していません。人口の変化は、出生と死亡だけによるものです。

• 瞬時の繁殖
  このモデルでは、生物が連続的かつ瞬時に繁殖すると仮定していますが、これは特に人間には現実的ではありません。

Pythonを使用したマルサスモデルのプロット

Pythonを使用してマルサスモデルをプロットする方法を示します。この可視化により、人口が時間とともにどのように変化するかをグラフで表現します。

以下は、マルサスモデルをプロットするPythonスクリプトです。

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

def malthusian_model(p0, r, t):
    return p0 * np.exp(r * t)

# Set the style using seaborn
sns.set()

# Parameters for the Malthusian model
p0 = 100     # Initial population size
r = 0.1      # Intrinsic growth rate

# Create an array of time values
time_values = np.linspace(0, 50, 100)

# Calculate the population size for each time value
population_sizes = malthusian_model(p0, r, time_values)

# Plotting
plt.figure(figsize=(10, 6))
plt.plot(time_values, population_sizes, label='Malthusian Model')
plt.xlabel('Time')
plt.ylabel('Population Size')
plt.title('Malthusian Model of Population Growth')
plt.legend()
plt.grid(True)
plt.show()

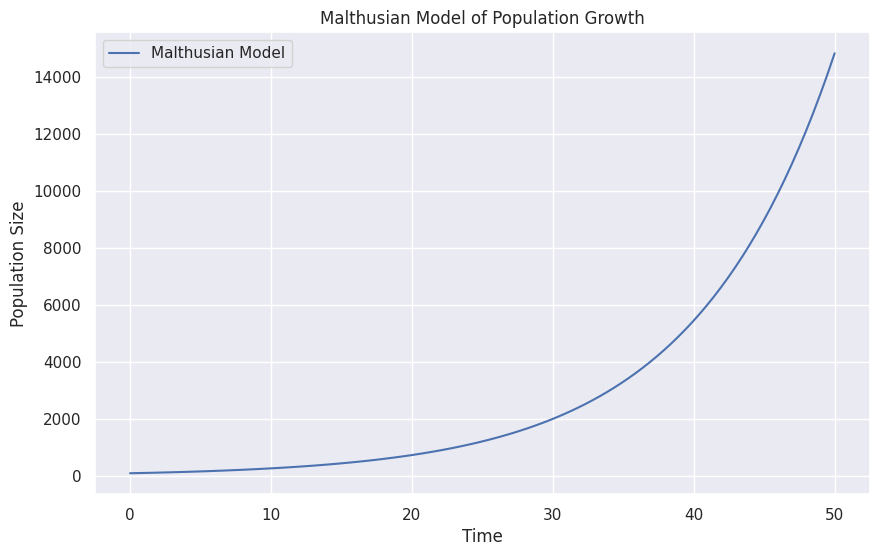
このコードによって、マルサスモデルに基づいて人口サイズが時間とともにどのように変化するかを示すプロットが生成されます。