2022-10-20

サポートベクターマシン（SVM）

Machine Learning

Classification

Python

sklearn

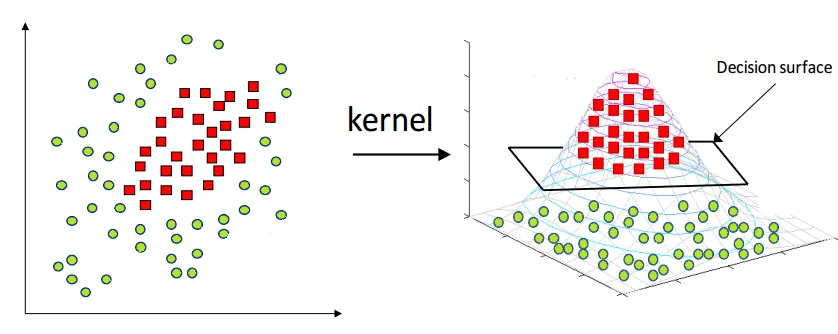
サポートベクターマシン（SVM）とは

サポートベクターマシン（SVM）は、分類に使用される強力な機械学習アルゴリズムです。SVMは、異なるクラスのデータポイントを最大マージンで分離する最適な特徴量空間内のハイパープレーンを見つけようとする非確率的なバイナリ線形分類器です。ハイパープレーンは、データポイントを最適に分離するように選択され、マージンはハイパープレーンと各クラスのもっとも近いデータポイントとの距離として定義されます。

線形に分離可能なデータに加えて、SVMはカーネルトリックを使用して非線形に分離可能なデータを処理することもできます。カーネルトリックにより、入力データを線形に分離できるようなより高次元の特徴量空間にマッピングします。SVMは、このより高次元の特徴量空間で最適なハイパープレーンを見つけて、データポイントを分離しようとします。

基本的な概念と用語

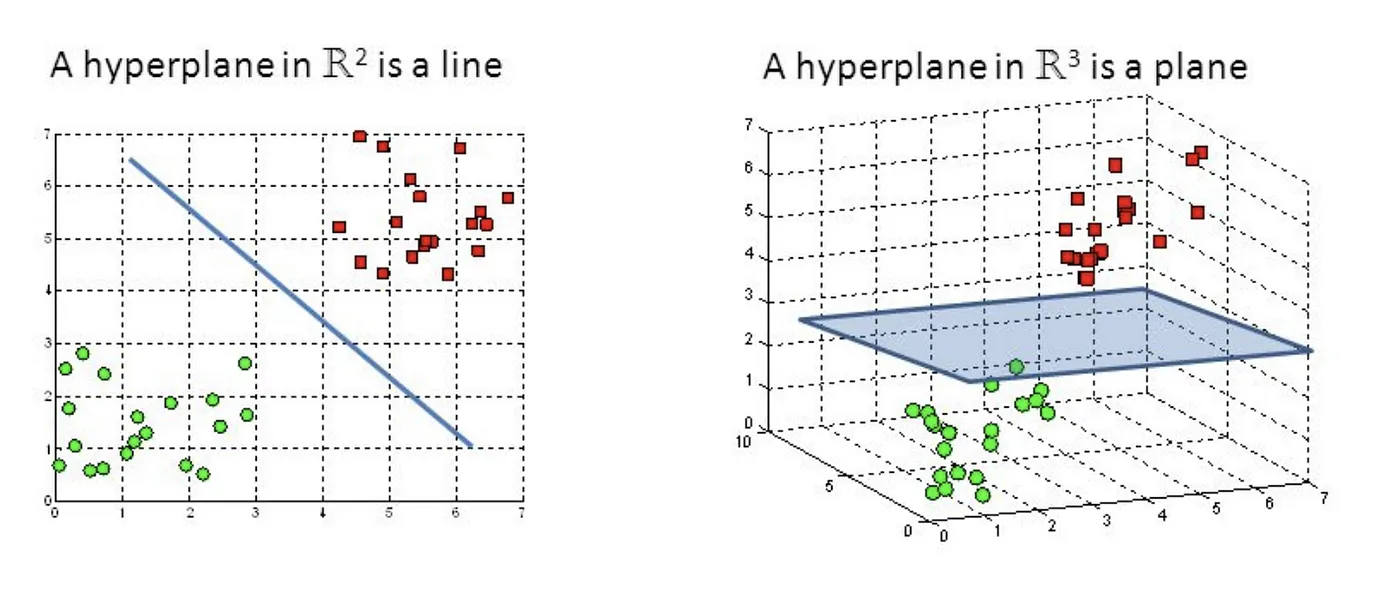
ハイパープレーン
ハイパープレーンは、直線（2D）または平面（3D）の概念を高次元空間に一般化した幾何学的オブジェクトです。n次元空間では、ハイパープレーンは(n-1)次元のオブジェクトとして定義されます。

Hyperplane
Support Vector Machine — Introduction to Machine Learning Algorithms

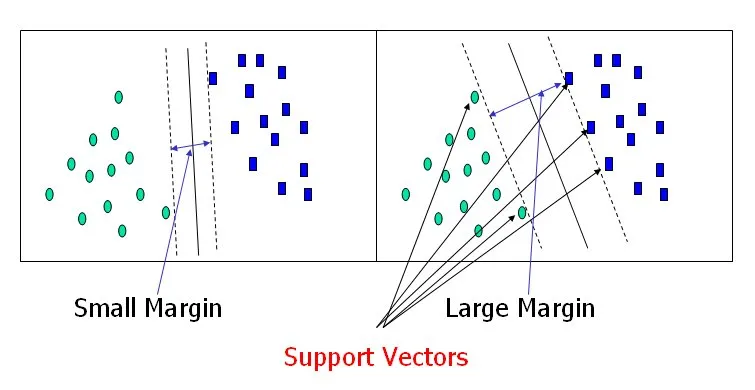
マージン
マージンは、異なるクラスのもっとも近いデータポイントと分離ハイパープレーンとの距離です。SVMの目的は、このマージンを最大化するハイパープレーンを見つけることで、より良い汎化能力を提供します。
サポートベクター
サポートベクターは、分離ハイパープレーンにもっとも近いデータポイントで、マージンを定義するのに重要な役割を果たします。これらのデータポイントは、ハイパープレーンの位置を決定する上で重要です。

Support Vector Machine — Introduction to Machine Learning Algorithms

線形分離性
データセットが線形分離可能である場合、異なるクラスのデータポイントを完全に分離することができるハイパープレーンが存在すると言われます。
カーネル関数
カーネル関数は、元のデータポイントを高次元の特徴量空間に写像し、SVMアルゴリズムが非線形分離可能なデータを扱うことを可能にします。

What is the kernel trick? Why is it important?

SVMの数学的理論

線形分離とハイパープレーン

n次元の特徴量ベクトルを持つデータセットが与えられた場合、ハイパープレーンは次式で表される(n-1)次元オブジェクトとして定義されます。

\boldsymbol{w} \cdot \boldsymbol{x} + b = 0

ここで、 $\boldsymbol{w}$ は重みベクトル、 $\boldsymbol{x}$ は特徴量ベクトル、 $b$ はバイアス項です。SVMの目的は、異なるクラスのデータポイントを分離する最適なハイパープレーンを見つけることです。

マージンの最大化

マージン( $M$ )は、異なるクラスのもっとも近いデータポイント（サポートベクター）とハイパープレーンとの距離です。クラスラベル $y_i \in {-1, 1}$ を持つデータポイント $\boldsymbol{x}_i$ に対して、ハイパープレーンの方程式は次式で表されます。

y_i(\boldsymbol{w} \cdot \boldsymbol{x}_i + b) = 1

データポイント $\boldsymbol{x}_i$ からハイパープレーンへの距離は次のようになります。

\frac{(\boldsymbol{w} \cdot \boldsymbol{x}_i) + b}{||\boldsymbol{w}||}

マージンは、ハイパープレーンと異なるクラスのデータポイントの最小距離であるため、以下が成立します。

M = \frac{1}{||\boldsymbol{w}||}

SVMの目的は、分類制約を維持しながらマージン $M$ を最大化することです。

y_i(\boldsymbol{w} \cdot \boldsymbol{x}_i + b) \geq 1, \quad \forall i

マージン $M$ の最大化は、重みベクトル $||\boldsymbol{w}||^2$ の二乗ノルムを最小化することと等価です。

双対問題とラグランジュ乗数法

制約最適化問題を解決するために、ラグランジュ乗数法を使用できます。SVM最適化問題のラグランジュアンは次式で表されます。

\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} ||\boldsymbol{w}||^2 - \sum_{i=1}^{N} \alpha_i \left[y_i(\boldsymbol{w} \cdot \boldsymbol{x}_i + b) - 1 \right]

ここで、 $N$ はデータポイントの数であり、 $\boldsymbol{\alpha}$ はラグランジュ乗数のベクトルです。

$\boldsymbol{w}$ と $b$ に関して $\mathcal{L}(\boldsymbol{w}, b, \boldsymbol{\alpha})$ を最小化し、 $\boldsymbol{\alpha}$ に関して最大化する必要があります。サドルポイント条件により以下が導かれます。

\frac{\partial \mathcal{L}}{\partial \boldsymbol{w}} = \boldsymbol{w} - \sum_{i=1}^{N} \alpha_i y_i \boldsymbol{x}_i = 0

そして、

\frac{\partial \mathcal{L}}{\partial b} = \sum_{i=1}^{N} \alpha_i y_i = 0

これらの条件をラグランジュアンに代入することで、次の双対最適化問題を得ます。

\max_{\boldsymbol{\alpha}} \left[\sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j (\boldsymbol{x}_i \cdot \boldsymbol{x}_j) \right]

ここで、制約条件は次のようになります。

\alpha_i \geq 0, \quad \forall i

\sum_{i=1}^{N} \alpha_i y_i = 0

このデュアル問題は二次計画問題であり、Sequential Minimal Optimization (SMO)アルゴリズムや勾配ベースの方法などのさまざまな最適化手法を用いて解くことができます。

カーネルトリック

データが線形的に分離できない場合、SVMはカーネルトリックを使用してデータを高次元空間に変換し、線形的に分離できるようにします。カーネル関数 $K(\boldsymbol{x}_i, \boldsymbol{x}_j)$ を使用して、元のデータポイントを新しい特徴量空間に写像し、SVMアルゴリズムが最適な分離ハイパープレーンを見つけることができます。双対問題は次式で表されます。

\max_{\boldsymbol{\alpha}} \left[\sum_{i=1}^{N} \alpha_i - \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_i \alpha_j y_i y_j K(\boldsymbol{x}_i, \boldsymbol{x}_j) \right]

以前と同様の制約条件が適用されます。一部の人気のあるカーネル関数には、線形カーネル、多項式カーネル、放射基底関数（RBF）カーネル、シグモイドカーネルがあります。

双対問題を解決すると、重みベクトル $\boldsymbol{w}$ は次のように計算できます。

\boldsymbol{w} = \sum_{i=1}^{N} \alpha_i y_i \phi(\boldsymbol{x}_i)

ここで、 $\phi(\boldsymbol{x}_i)$ は高次元空間の写像された特徴量ベクトルです。バイアス項 $b$ は、任意のサポートベクター $\boldsymbol{x}_s$ を使用して次のように計算できます。

b = \frac{1}{y_s} - \sum_{i=1}^{N} \alpha_i y_i K(\boldsymbol{x}_i, \boldsymbol{x}_s)

新しいデータポイント $\boldsymbol{x}^*$ の決定関数は次のようになります。

f(\boldsymbol{x}^*) = \operatorname{sign} \left( \sum_{i=1}^{N} \alpha_i y_i K(\boldsymbol{x}_i, \boldsymbol{x}^*) + b \right)

カーネルトリックにより、SVMは非線形分離可能なデータを扱うことができ、適切なカーネル関数を選択することでアルゴリズムにドメイン知識を柔軟に組み込むことができます。

Irisデータセットを使用したSVMの実装

この章では、Pythonとscikit-learnライブラリを使用してSVMを実装します。様々なカーネルを使用したSVMの分類能力を示すために、Irisデータセットを使用します。

まず、必要なライブラリをインポートしてIrisデータセットをロードします。

python

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.svm import SVC
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix

# Load the Iris dataset
iris = datasets.load_iris()
X = iris.data[:, :2]  # We will only use the first two features for visualization purposes
y = iris.target

次に、データセットをトレーニングセットとテストセットに分割し、様々なカーネルを使用してSVMモデルをトレーニングします。

python

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)

# Define the kernel names and types
kernels = {
    'Linear': 'linear',
    'Polynomial': 'poly',
    'RBF': 'rbf',
    'Sigmoid': 'sigmoid'
}

# Train and evaluate the SVM model with different kernels
for name, kernel in kernels.items():
    svm = SVC(kernel=kernel, C=1, degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)
    svm.fit(X_train, y_train)
    y_pred = svm.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    print(f'{name} Kernel SVM Accuracy: {accuracy:.2f}')

Linear Kernel SVM Accuracy: 0.80
Polynomial Kernel SVM Accuracy: 0.73
RBF Kernel SVM Accuracy: 0.80
Sigmoid Kernel SVM Accuracy: 0.29

様々なカーネルの決定境界を可視化するための関数を作成し、結果をプロットしてみます。

python

def plot_svm_decision_boundary(svm, X, y, kernel, ax):
    h = .02  # Step size in the mesh
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))

    Z = svm.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    ax.contourf(xx, yy, Z, alpha=0.8, cmap=plt.cm.coolwarm)
    scatter = ax.scatter(X[:, 0], X[:, 1], c=y, edgecolors='k', marker='o', s=50, cmap=plt.cm.coolwarm)
    ax.set_xlabel('Feature 1')
    ax.set_ylabel('Feature 2')
    ax.set_title(f'{kernel} Kernel SVM')
    ax.legend(*scatter.legend_elements(), title="Classes")

# Create a figure and subplots for each kernel
fig, axes = plt.subplots(2, 2, figsize=(12, 12))
axes = axes.ravel()

# Plot the decision boundaries
for i, (name, kernel) in enumerate(kernels.items()):
    svm = SVC(kernel=kernel, C=1, degree=3, gamma='scale', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', break_ties=False, random_state=None)
    svm.fit(X_train, y_train)
    plot_svm_decision_boundary(svm, X_train, y_train, name, axes[i])

# Adjust plot layout and show the figure
plt.tight_layout()
plt.show()

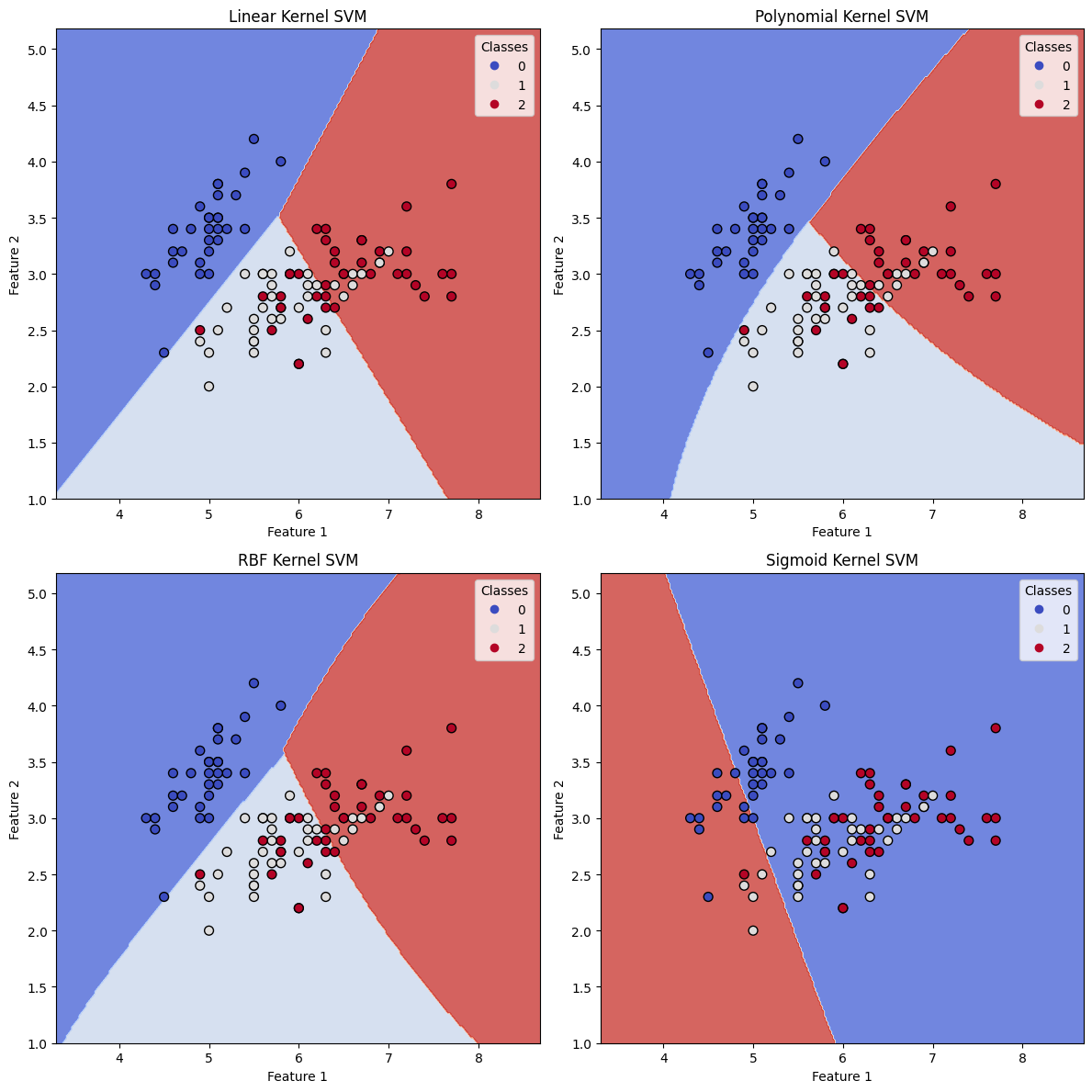
SVM plot

上記のコードを実行することで、異なるカーネルを使用したSVMモデルの決定境界を示す4つのプロットを得ることができます。プロットは、各カーネルが異なる決定境界を生み出すことが、結果的に分類結果に影響することを示しています。

線形カーネルは線形の決定境界を生み出し、非線形なパターンを持つ複雑なデータセットには適していない場合があります。
多項式カーネルは、曲線の決定境界を作成することでより柔軟性を持たせることができ、線形分離が不可能な場合にデータによりよく適合することができます。多項式の次数を調整して決定境界の複雑さを制御することができます。
RBF（Radial Basis Function）カーネルは、多くの分類問題で非常に人気があり、データ内の複雑で非線形なパターンを扱うことができます。決定境界は非常に滑らかで、データセットの基本構造に適応することができます。
シグモイドカーネルも非線形決定境界を作成することができますが、一般的にはRBFカーネルに比べて人気がありません。

精度スコアとプロットから、異なるカーネル関数がSVM分類器のパフォーマンスにどのように影響するかを観察することができます。データセットの性質や基本的なパターンに応じて、最適なカーネルを選択して最良の分類結果を得る必要があります。